Los 7 algoritmos de aprendizaje automático más utilizados en Python que debe conocer

El aprendizaje automático es una rama de la inteligencia artificial (IA) que se ocupa de los algoritmos informáticos que se utilizan en cualquier dato. Se enfoca en aprender automáticamente de los datos que se introducen en él y nos brinda resultados al mejorar las predicciones anteriores cada vez.

Principales algoritmos de aprendizaje automático utilizados en Python

A continuación se muestran algunos de los principales algoritmos de aprendizaje automático utilizados en Python, junto con fragmentos de código que muestran su implementación y visualizaciones de los límites de clasificación.

1. Regresión lineal

La regresión lineal es una de las técnicas de aprendizaje automático supervisado más utilizadas. Como su nombre indica, esta regresión trata de modelar la relación entre dos variables usando una ecuación lineal y ajustando esa línea a los datos observados. Esta técnica se utiliza para estimar valores continuos reales como las ventas totales realizadas o el costo de las casas.

La línea de mejor ajuste también se llama línea de regresión. Está dada por la siguiente ecuación:

Y = a*X + b

donde Y es la variable dependiente, a es la pendiente, X es la variable independiente y b es el valor del intercepto. Los coeficientes a y b se obtienen minimizando el cuadrado de la diferencia de esa distancia entre los distintos puntos de datos y la ecuación de la línea de regresión.

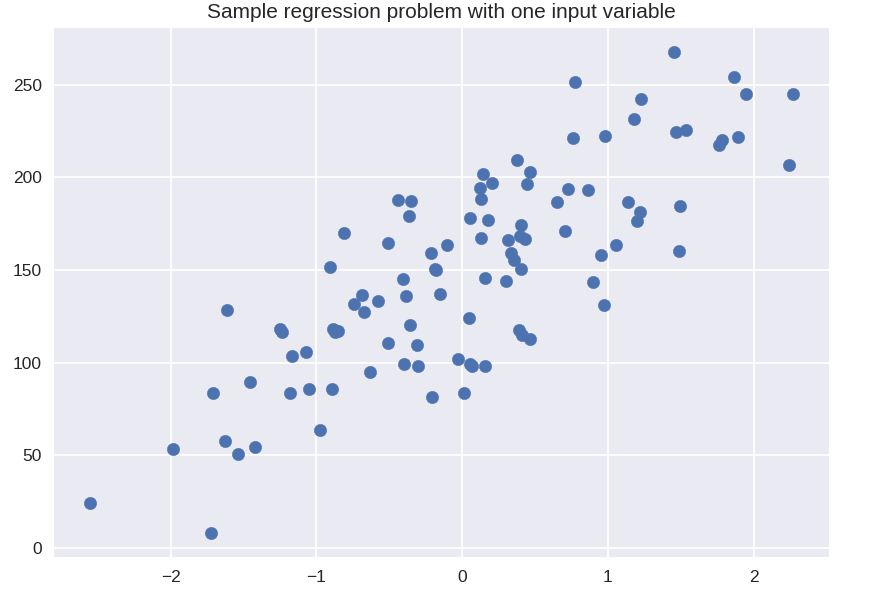
# conjunto de datos sintéticos para regresión simple

desde sklearn.datasets import make_regression

plt.figura()

plt.title('Problema de regresión de muestra con una variable de entrada')

X_R1, y_R1 = make_regression( n_samples = 100, n_features = 1, n_informative = 1, bias = 150.0, noise = 30, random_state = 0 )

plt.dispersión(X_R1, y_R1, marcador = 'o', s = 50)

plt.mostrar()

de sklearn.linear_model importar LinearRegression

X_train, X_test, y_train, y_test = train_test_split( X_R1, y_R1,

estado_aleatorio = 0 )

linreg = LinearRegression().fit( X_tren, y_tren )

print( 'modelo lineal coef (w): {}'.format( linreg.coef_ ) )

print( 'intersección del modelo lineal (b): {:.3f}'z.format( linreg.intercept_ ) )

print('Puntaje R-cuadrado (entrenamiento): {:.3f}'.format( linreg.score( X_train, y_train ) ) )

print( 'Puntaje R-cuadrado (prueba): {:.3f}'.format( linreg.score( X_test, y_test ) ) )

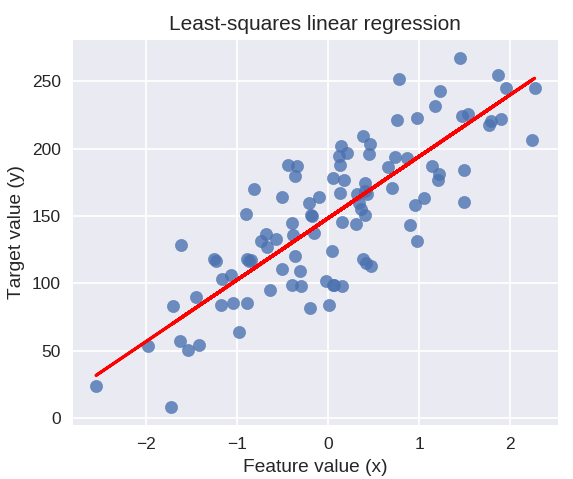
Producción

coeficiente del modelo lineal (w): [ 45.71]

intercepción del modelo lineal (b): 148.446

Puntuación R-cuadrado (entrenamiento): 0,679

Puntuación R-cuadrado (prueba): 0,492

El siguiente código dibujará la línea de regresión ajustada en el gráfico de nuestros puntos de datos.

plt.figure (tamaño de figura = (5, 4))

plt.scatter(X_R1, y_R1, marcador = 'o', s = 50, alfa = 0.8)

plt.plot( X_R1, linreg.coef_ * X_R1 + linreg.intercept_, 'r-' )

plt.title( 'Regresión lineal de mínimos cuadrados' )

plt.xlabel('Valor de la característica (x)')

plt.ylabel('Valor objetivo (y)')

plt.mostrar()

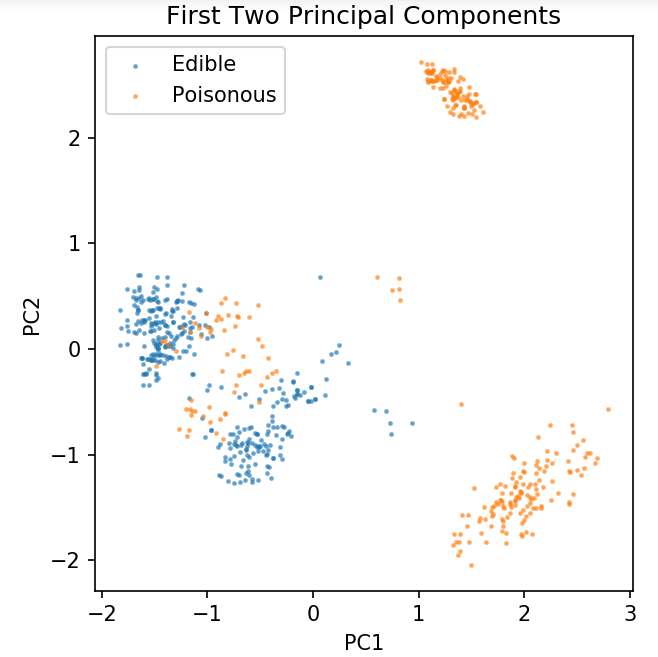
Preparación de un conjunto de datos común para explorar técnicas de clasificación

Los siguientes datos se utilizarán para mostrar los diversos algoritmos de clasificación que se utilizan con mayor frecuencia en el aprendizaje automático en Python.

El conjunto de datos de hongos UCI se almacena en hongos.csv.

Cuaderno %matplotlib

importar pandas como pd

importar numpy como np

importar matplotlib.pyplot como plt

de sklearn.descomposición importar PCA

de sklearn.model_selection import train_test_split

df = pd.read_csv( 'solo lectura/hongos.csv' )

df2 = pd.get_dummies( df )

df3 = df2.muestra (fracción = 0,08)

X = df3.iloc[:, 2:]

y = df3.iloc[:, 1]

pca = PCA( n_componentes = 2 ).fit_transform( X )

X_train, X_test, y_train, y_test = train_test_split( pca, y, random_state = 0 )

plt.figura (ppp = 120)

plt.scatter( pca[y.values ​​== 0, 0], pca[y.values ​​== 0, 1], alpha = 0.5, label = 'Comestible', s = 2 )

plt.scatter( pca[y.values ​​== 1, 0], pca[y.values ​​== 1, 1], alpha = 0.5, label = 'Venenoso', s = 2 )

plt.leyenda()

plt.title('Conjunto de datos de hongos\nPrimeros dos componentes principales')

plt.xlabel('PC1')

plt.ylabel('PC2')

plt.gca().set_aspect('igual')

Usaremos la función definida a continuación para obtener los límites de decisión de los diferentes clasificadores que usaremos en el conjunto de datos de hongos.

def plot_mushroom_boundary( X, y, modelo_ajustado ):

plt.figure( figsize = (9.8, 5), dpi = 100 )

para i, plot_type en enumerate( ['Límite de decisión', 'Probabilidades de decisión'] ):

plt.subtrama( 1, 2, i + 1 )

mesh_step_size = 0.01 # tamaño de paso en la malla

x_min, x_max = X[:, 0].min() – .1, X[:, 0].max() + .1

y_min, y_max = X[:, 1].min() – .1, X[:, 1].max() + .1

xx, yy = np.meshgrid( np.arange( x_min, x_max, mesh_step_size ), np.arange( y_min, y_max, mesh_step_size ) )

si yo == 0:

Z = modelo_ajustado.predecir( np.c_[xx.ravel(), yy.ravel()] )

demás:

tratar:

Z = modelo_ajustado.predict_proba( np.c_[xx.ravel(), yy.ravel()] )[:, 1]

excepto:

plt.text( 0.4, 0.5, 'Probabilidades no disponibles', horizontalalignment = 'center', verticalalignment = 'center', transform = plt.gca().transAxes, fontsize = 12 )

plt.eje('apagado')

descanso

Z = Z.reforma( xx.forma )

plt.scatter( X[y.values ​​== 0, 0], X[y.values ​​== 0, 1], alpha = 0.4, label = 'Comestible', s = 5 )

plt.scatter( X[y.values ​​== 1, 0], X[y.values ​​== 1, 1], alpha = 0.4, label = 'Posionous', s = 5 )

plt.imshow( Z, interpolación = 'más cercano', cmap = 'RdYlBu_r', alfa = 0,15, extensión = (x_min, x_max, y_min, y_max), origen = 'inferior')

plt.title( plot_type + '\n' + str( modelo_ajustado ).split( '(' )[0] + ' Precisión de la prueba: ' + str( np.round( modelo_ajustado.puntuación( X, y ), 5 ) ) )

plt.gca().set_aspect('igual');

plt.tight_layout()

plt.subplots_adjust( arriba = 0.9, abajo = 0.08, wspace = 0.02 )

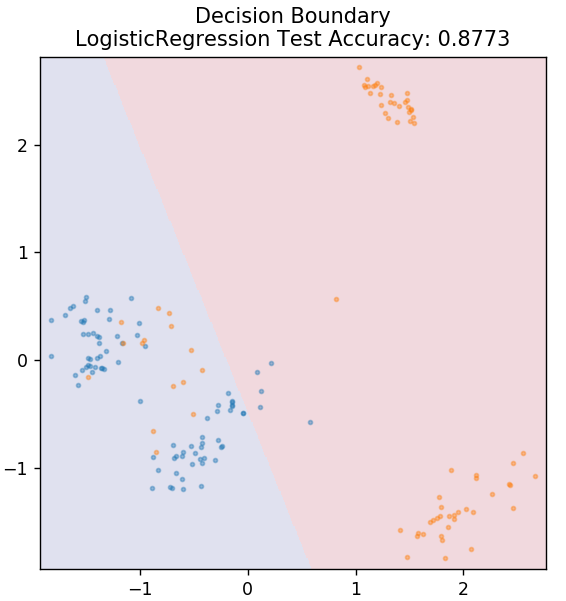
2. Regresión logística

A diferencia de la regresión lineal, la regresión logística se ocupa de la estimación de valores discretos (0/1 valores binarios, verdadero/falso, sí/no). Esta técnica también se llama regresión logit. Esto se debe a que predice la probabilidad de un evento mediante el uso de una función logit para entrenar los datos dados. Su valor siempre está entre 0 y 1 (ya que está calculando una probabilidad).

El logaritmo de las probabilidades de los resultados se construye como una combinación lineal de la variable predictora de la siguiente manera:

probabilidades = p / (1 – p) = probabilidad de que ocurra el evento o probabilidad de que no ocurra el evento

ln( probabilidades ) = ln( p / (1 – p) )

logit( p ) = ln( p / (1 – p) ) = b0 + b1X1 + b2X2 + b3X3 + … + bkXk

donde p es la probabilidad de presencia de una característica.

de sklearn.linear_model import LogisticRegression

modelo = LogisticRegression()

modelo.fit( X_tren, y_tren )

plot_mushroom_boundary( X_test, y_test, modelo )

Obtenga la certificación de inteligencia artificial en línea de las mejores universidades del mundo: maestrías, programas ejecutivos de posgrado y programa de certificado avanzado en ML e IA para acelerar su carrera.

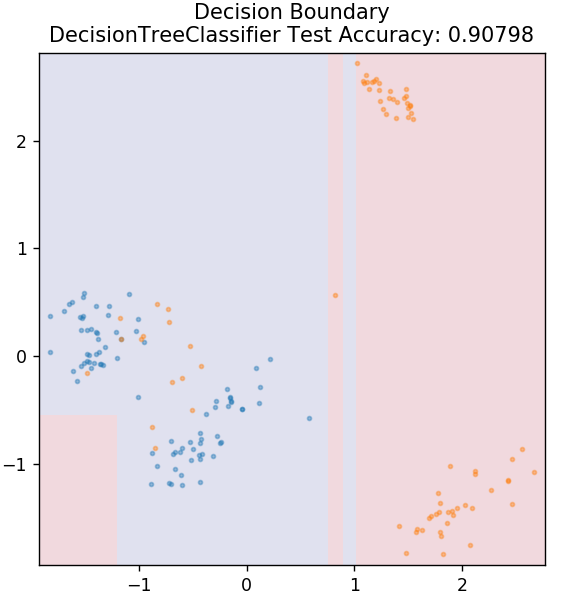
3. Árbol de decisión

Este es un algoritmo muy popular que se puede utilizar para clasificar variables de datos continuas y discretas. En cada paso, los datos se dividen en más de un conjunto homogéneo en función de algún atributo/condiciones de división.

de sklearn.tree importar DecisionTreeClassifier

modelo = DecisionTreeClassifier (máx_profundidad = 3)

modelo.fit( X_tren, y_tren )

plot_mushroom_boundary( X_test, y_test, modelo )

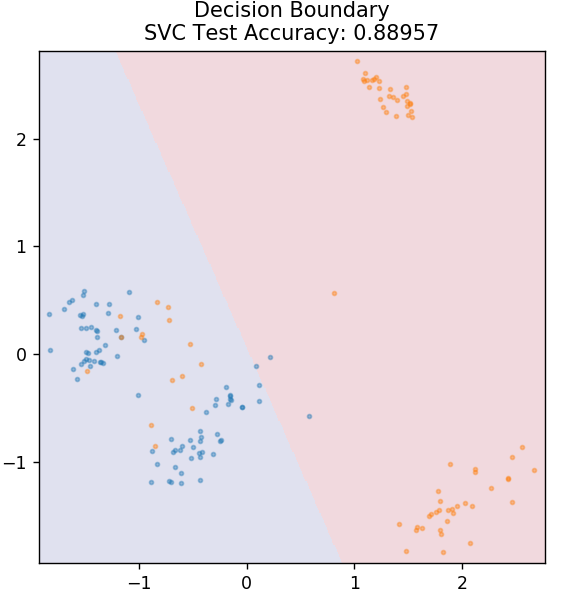
4. MVS

SVM es la abreviatura de Support Vector Machines. Aquí la idea básica es clasificar los puntos de datos usando hiperplanos para la separación. El objetivo es encontrar un hiperplano que tenga la máxima distancia (o margen) entre los puntos de datos de ambas clases o categorías.

Elegimos el plano de tal manera que nos encarguemos de clasificar los puntos desconocidos en el futuro con la máxima confianza. Las SVM se utilizan de manera famosa porque brindan una alta precisión y consumen muy poca potencia computacional. Las SVM también se pueden usar para problemas de regresión.

desde sklearn.svm importar SVC

modelo = SVC (núcleo = 'lineal')

modelo.fit( X_tren, y_tren )

plot_mushroom_boundary( X_test, y_test, modelo )

Pago: Proyectos de Python en GitHub

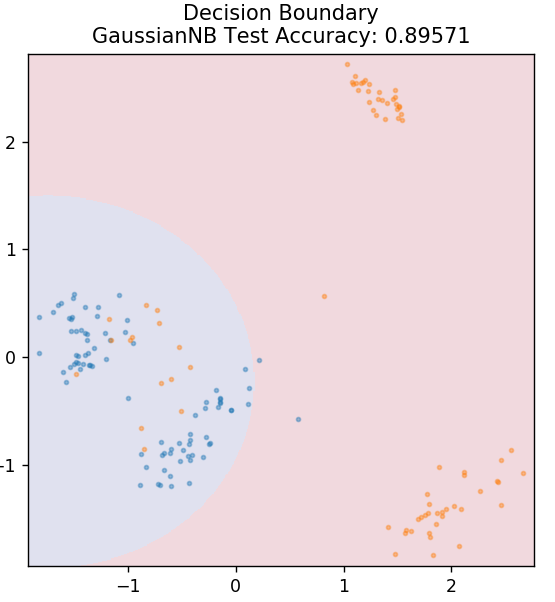
5. Bayesiano ingenuo

Como su nombre indica, el algoritmo Naive Bayes es un algoritmo de aprendizaje supervisado basado en el Teorema de Bayes . El Teorema de Bayes usa probabilidades condicionales para darte la probabilidad de un evento basado en algún conocimiento dado.

Donde,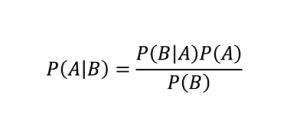

P (A | B): La probabilidad condicional de que ocurra el evento A, dado que el evento B ya ocurrió. (También llamada probabilidad posterior)

P(A): Probabilidad del evento A.

P(B): Probabilidad del evento B.

P (B | A): La probabilidad condicional de que ocurra el evento B, dado que el evento A ya ocurrió.

¿Por qué este algoritmo se llama Naive? Esto se debe a que asume que todas las ocurrencias de eventos son independientes entre sí. Entonces, cada característica define por separado la clase a la que pertenece un punto de datos, sin tener ninguna dependencia entre ellos. Naive Bayes es la mejor opción para las categorizaciones de texto. Funcionará lo suficientemente bien incluso con pequeñas cantidades de datos de entrenamiento.

de sklearn.naive_bayes importar GaussianNB

modelo = GaussianNB()

modelo.fit( X_tren, y_tren )

plot_mushroom_boundary( X_test, y_test, modelo )

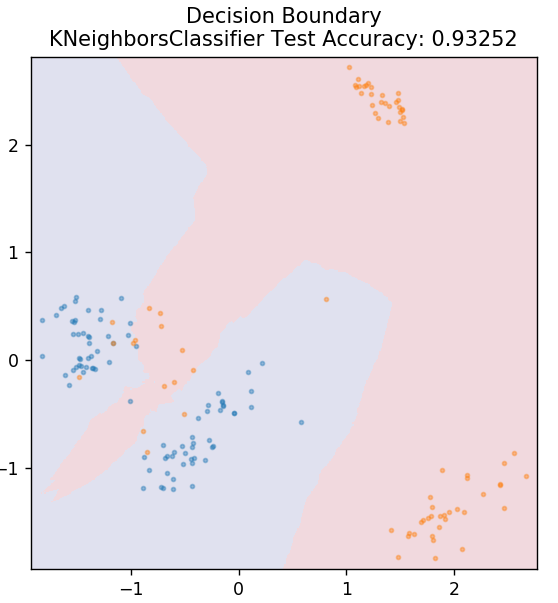
5. KNN

KNN significa K-vecinos más cercanos. Es un algoritmo de aprendizaje supervisado de uso muy extendido que clasifica los datos de prueba según sus similitudes con los datos de entrenamiento previamente clasificados. KNN no clasifica todos los puntos de datos durante el entrenamiento. En cambio, simplemente almacena el conjunto de datos y cuando obtiene datos nuevos, clasifica esos puntos de datos en función de sus similitudes. Lo hace calculando la distancia euclidiana del número K de vecinos más cercanos (aquí, n_neighbors ) de ese punto de datos.

de sklearn.neighbors importar KNeighborsClassifier

modelo = KNeighborsClassifier( n_neighbors = 20 )

modelo.fit( X_tren, y_tren )

plot_mushroom_boundary( X_test, y_test, modelo )

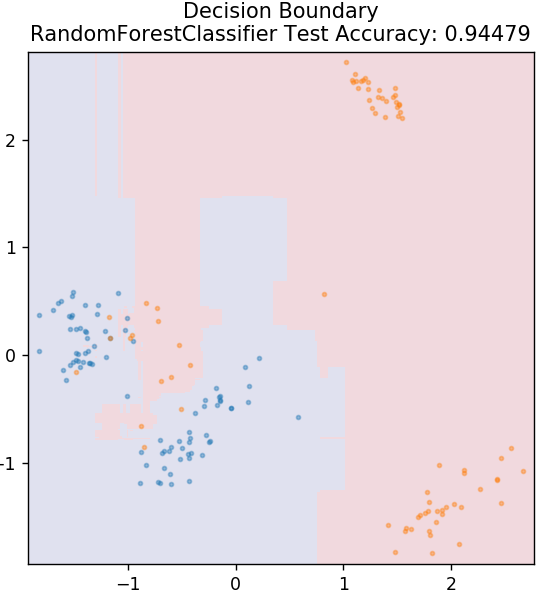
6. Bosque aleatorio

Random forest es un algoritmo de aprendizaje automático muy simple y diverso que utiliza una técnica de aprendizaje supervisado. Como puede adivinar por el nombre, el bosque aleatorio consta de una gran cantidad de árboles de decisión que actúan como un conjunto. Cada árbol de decisión determinará la clase de salida de los puntos de datos y la clase mayoritaria se elegirá como la salida final del modelo. La idea aquí es que más árboles que trabajen con los mismos datos tenderán a ser más precisos en los resultados que los árboles individuales.

de sklearn.ensemble importar RandomForestClassifier

modelo = RandomForestClassifier()

modelo.fit( X_tren, y_tren )

plot_mushroom_boundary( X_test, y_test, modelo )

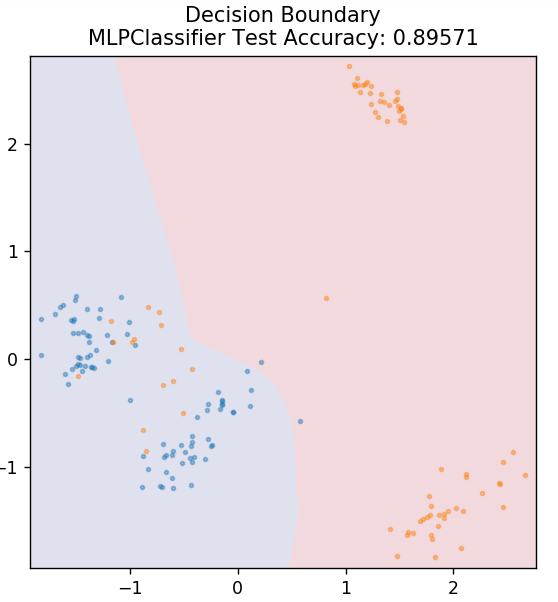
7. Perceptrón multicapa

Multi-Layer Perceptron (o MLP) es un algoritmo muy fascinante que pertenece a la rama del aprendizaje profundo. Más específicamente, pertenece a la clase de redes neuronales artificiales feed-forward (ANN). MLP forma una red de múltiples perceptrones con al menos tres capas: una capa de entrada, una capa de salida y una capa oculta. Los MLP pueden distinguir entre datos que no son separables linealmente.

Cada neurona en las capas ocultas utiliza una función de activación para pasar a la siguiente capa. Aquí, el algoritmo de retropropagación se usa para ajustar los parámetros y, por lo tanto, entrenar la red neuronal. Se puede utilizar principalmente para problemas de regresión simples.

de sklearn.neural_network importar MLPClassifier

modelo = MLPClassifier()

modelo.fit( X_tren, y_tren )

plot_mushroom_boundary( X_test, y_test, modelo )

Lea también: Ideas y temas de proyectos de Python

Conclusión

Podemos concluir que diferentes algoritmos de aprendizaje automático producen diferentes límites de decisión y, por lo tanto, diferentes resultados de precisión al clasificar el mismo conjunto de datos.

No hay forma de declarar a nadie algoritmo como el mejor algoritmo para todo tipo de datos en general. El aprendizaje automático requiere pruebas y errores rigurosos para que varios algoritmos determinen qué funciona mejor para cada conjunto de datos por separado. La lista de algoritmos de ML obviamente no termina aquí. Existe un vasto mar de otras técnicas que esperan ser exploradas en la biblioteca Scikit-Learn de Python. ¡Continúe y entrene sus conjuntos de datos usando todos esos y diviértase!

Si está interesado en obtener más información sobre árboles de decisión, aprendizaje automático, consulte el Programa PG Ejecutivo en Aprendizaje Automático e IA de IIIT-B y upGrad, que está diseñado para profesionales que trabajan y ofrece más de 450 horas de capacitación rigurosa, más de 30 estudios de casos y asignaciones, estado de exalumno de IIIT-B, más de 5 proyectos prácticos finales prácticos y asistencia laboral con las mejores empresas.