25 preguntas y respuestas de la entrevista sobre aprendizaje automático: regresión lineal
Publicado: 2022-09-08Es una práctica común evaluar a los aspirantes a la ciencia de datos en algoritmos de aprendizaje automático de uso común en entrevistas. Estos algoritmos convencionales son regresión lineal, regresión logística, agrupación, árboles de decisión, etc. Se espera que los científicos de datos posean un conocimiento profundo de estos algoritmos.
Consultamos a gerentes de contratación y científicos de datos de varias organizaciones para conocer las preguntas típicas de ML que hacen en una entrevista. En base a sus extensos comentarios, se preparó un conjunto de preguntas y respuestas para ayudar a los aspirantes a científicos de datos en sus conversaciones. Las preguntas de la entrevista de regresión lineal son las más comunes en las entrevistas de aprendizaje automático. Las preguntas y respuestas sobre estos algoritmos se proporcionarán en una serie de cuatro publicaciones de blog.
Los mejores cursos de aprendizaje automático y cursos de inteligencia artificial en línea
| Maestría en Ciencias en Aprendizaje Automático e IA de LJMU | Programa Ejecutivo de Postgrado en Aprendizaje Automático e IA del IIITB | |
| Programa de Certificado Avanzado en Aprendizaje Automático y PNL de IIITB | Programa de Certificado Avanzado en Aprendizaje Automático y Aprendizaje Profundo de IIITB | Programa ejecutivo de posgrado en ciencia de datos y aprendizaje automático de la Universidad de Maryland |
| Para explorar todos nuestros cursos, visite nuestra página a continuación. | ||
| Cursos de aprendizaje automático | ||
Cada publicación de blog cubrirá el siguiente tema: -
- Regresión lineal
- Regresión logística
- Agrupación
- Árboles de decisión y preguntas que pertenecen a todos los algoritmos
¡Comencemos con la regresión lineal!
1. ¿Qué es la regresión lineal?
En términos simples, la regresión lineal es un método para encontrar la mejor línea recta que se ajuste a los datos dados, es decir, encontrar la mejor relación lineal entre las variables independientes y dependientes.
En términos técnicos, la regresión lineal es un algoritmo de aprendizaje automático que encuentra la mejor relación de ajuste lineal en cualquier dato dado, entre variables independientes y dependientes. Se realiza principalmente por el método de la suma de los residuos al cuadrado.
Habilidades de aprendizaje automático bajo demanda
| Cursos de Inteligencia Artificial | Cursos de Tableau |
| Cursos de PNL | Cursos de aprendizaje profundo |

2. Enunciar los supuestos en un modelo de regresión lineal.
Hay tres supuestos principales en un modelo de regresión lineal:
- La suposición sobre la forma del modelo:
Se supone que existe una relación lineal entre las variables dependientes e independientes. Se conoce como el 'supuesto de linealidad'. - Suposiciones sobre los residuos:
- Suposición de normalidad: se supone que los términos de error, ε (i) , se distribuyen normalmente.
- Suposición de media cero: Se supone que los residuos tienen un valor medio de cero.
- Suposición de varianza constante: Se supone que los términos residuales tienen la misma varianza (pero desconocida), σ 2 Esta suposición también se conoce como suposición de homogeneidad u homocedasticidad.
- Suposición de error independiente: Se supone que los términos residuales son independientes entre sí, es decir, su covarianza por pares es cero.
- Suposiciones sobre los estimadores:
- Las variables independientes se miden sin error.
- Las variables independientes son linealmente independientes entre sí, es decir, no hay multicolinealidad en los datos.
Explicación:
- Esto se explica por sí mismo.
- Si los residuos no se distribuyen normalmente, se pierde su aleatoriedad, lo que implica que el modelo no es capaz de explicar la relación en los datos.
Además, la media de los residuos debe ser cero.
Y (i)i = β 0 + β 1 x (i) + ε (i)
Este es el modelo lineal asumido, donde ε es el término residual.
E(Y) = E( β 0 + β 1 x (i) + ε (i) )
= E( β 0 + β 1 x (i) + ε (i) )
Si la expectativa (media) de los residuos, E(ε (i) ), es cero, las expectativas de la variable objetivo y el modelo se vuelven iguales, que es uno de los objetivos del modelo.
Los residuos (también conocidos como términos de error) deben ser independientes. Esto significa que no hay correlación entre los residuos y los valores pronosticados, o entre los residuos mismos. Si alguna correlación está presente, implica que existe alguna relación que el modelo de regresión no puede identificar. - Si las variables independientes no son linealmente independientes entre sí, se pierde la unicidad de la solución de mínimos cuadrados (o solución de ecuación normal).
Únase al curso de inteligencia artificial en línea de las mejores universidades del mundo: maestrías, programas ejecutivos de posgrado y programa de certificado avanzado en ML e IA para acelerar su carrera.
3. ¿Qué es la ingeniería de características? ¿Cómo lo aplicas en el proceso de modelado?
La ingeniería de características es el proceso de transformar datos sin procesar en características que representen mejor el problema subyacente a los modelos predictivos.
, lo que da como resultado una mayor precisión del modelo en datos no vistos.
En términos simples, la ingeniería de funciones significa el desarrollo de nuevas funciones que pueden ayudarlo a comprender y modelar el problema de una mejor manera. La ingeniería de características es de dos tipos: impulsada por el negocio e impulsada por los datos. La ingeniería de características impulsada por el negocio gira en torno a la inclusión de características desde un punto de vista comercial. El trabajo aquí es transformar las variables comerciales en características del problema. En el caso de la ingeniería de características basada en datos, las características que agrega no tienen ninguna interpretación física significativa, pero ayudan al modelo en la predicción de la variable de destino.
FYI: ¡Curso de PNL gratis!
Para aplicar la ingeniería de características, uno debe estar completamente familiarizado con el conjunto de datos. Esto implica saber cuáles son los datos dados, qué significan, cuáles son las características sin procesar, etc. También debe tener una idea clara del problema, como qué factores afectan la variable objetivo, cuál es la interpretación física de la variable. , etc.
4. ¿Para qué sirve la regularización? Explicar las regularizaciones de L1 y L2.
La regularización es una técnica que se utiliza para abordar el problema del sobreajuste del modelo. Cuando se implementa un modelo muy complejo en los datos de entrenamiento, se sobreajusta. A veces, es posible que el modelo simple no pueda generalizar los datos y el modelo complejo se sobreajuste. Para abordar este problema, se utiliza la regularización.
La regularización no es más que agregar los términos de los coeficientes (betas) a la función de costo para que los términos se penalicen y sean de pequeña magnitud. Básicamente, esto ayuda a capturar las tendencias en los datos y, al mismo tiempo, evita el sobreajuste al no permitir que el modelo se vuelva demasiado complejo.
- Regularización L1 o LASSO: Aquí, los valores absolutos de los coeficientes se suman a la función de coste. Esto se puede ver en la siguiente ecuación; la parte resaltada corresponde a la regularización L1 o LASSO. Esta técnica de regularización brinda resultados escasos, lo que también conduce a la selección de características.
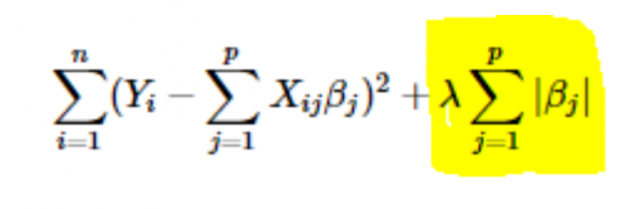
- Regularización L2 o Ridge: Aquí, los cuadrados de los coeficientes se suman a la función de costo. Esto se puede ver en la siguiente ecuación, donde la parte resaltada corresponde a la regularización L2 o Ridge.
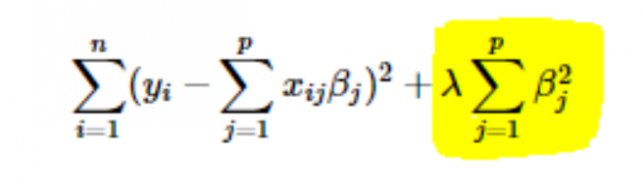
5. ¿Cómo elegir el valor de la tasa de aprendizaje del parámetro (α)?
Seleccionar el valor de la tasa de aprendizaje es un asunto complicado. Si el valor es demasiado pequeño, el algoritmo de descenso de gradiente tarda años en converger a la solución óptima. Por otro lado, si el valor de la tasa de aprendizaje es alto, el descenso del gradiente sobrepasará la solución óptima y lo más probable es que nunca converja a la solución óptima.
Para superar este problema, puede probar diferentes valores de alfa en un rango de valores y graficar el costo frente al número de iteraciones. Luego, en base a los gráficos, se puede elegir el valor correspondiente al gráfico que muestra la rápida disminución. 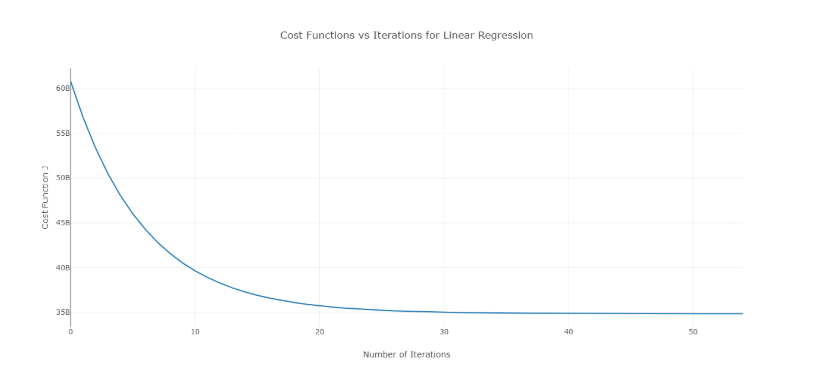
La gráfica antes mencionada es una curva ideal de costo vs el número de iteraciones. Tenga en cuenta que el costo inicialmente disminuye a medida que aumenta el número de iteraciones, pero después de ciertas iteraciones, el descenso del gradiente converge y el costo ya no disminuye.
Si ve que el costo aumenta con la cantidad de iteraciones, su parámetro de tasa de aprendizaje es alto y debe reducirse.
6. ¿Cómo elegir el valor del parámetro de regularización (λ)?
Seleccionar el parámetro de regularización es un asunto complicado. Si el valor de λ es demasiado alto, dará lugar a valores extremadamente pequeños del coeficiente de regresión β , lo que provocará un ajuste insuficiente del modelo (sesgo alto - varianza baja). Por otro lado, si el valor de λ es 0 (muy pequeño), el modelo tenderá a sobreajustarse a los datos de entrenamiento (sesgo bajo – varianza alta).
No existe una forma adecuada de seleccionar el valor de λ . Lo que puede hacer es tener una submuestra de datos y ejecutar el algoritmo varias veces en diferentes conjuntos. Aquí, la persona tiene que decidir cuánta variación puede tolerar. Una vez que el usuario está satisfecho con la varianza, se puede elegir ese valor de λ para el conjunto de datos completo.
Una cosa a tener en cuenta es que el valor de λ seleccionado aquí fue óptimo para ese subconjunto, no para todos los datos de entrenamiento.
7. ¿Podemos usar la regresión lineal para el análisis de series de tiempo?
Se puede utilizar la regresión lineal para el análisis de series de tiempo, pero los resultados no son prometedores. Por lo tanto, generalmente no es recomendable hacerlo. Las razones detrás de esto son:
- Los datos de series temporales se utilizan principalmente para la predicción del futuro, pero la regresión lineal rara vez da buenos resultados para la predicción futura, ya que no está diseñada para la extrapolación.
- En su mayoría, los datos de series temporales tienen un patrón, como durante las horas pico, las temporadas festivas, etc., que muy probablemente se tratarían como valores atípicos en el análisis de regresión lineal.
8. ¿A qué valor se acerca la suma de los residuos de una regresión lineal? Justificar.
Respuesta La suma de los residuos de una regresión lineal es 0. La regresión lineal funciona suponiendo que los errores (residuales) se distribuyen normalmente con una media de 0, es decir
Y = β T X + ε
Aquí, Y es la variable objetivo o dependiente,
β es el vector del coeficiente de regresión,
X es la matriz de características que contiene todas las características como columnas,
ε es el término residual tal que ε ~ N(0,σ 2 ).
Entonces, la suma de todos los residuos es el valor esperado de los residuos multiplicado por el número total de puntos de datos. Dado que la expectativa de residuos es 0, la suma de todos los términos residuales es cero.
Nota : N(μ,σ 2 ) es la notación estándar para una distribución normal que tiene media μ y desviación estándar σ 2 .
9. ¿Cómo afecta la multicolinealidad a la regresión lineal?
Ans La multicolinealidad ocurre cuando algunas de las variables independientes están altamente correlacionadas (positiva o negativamente) entre sí. Esta multicolinealidad causa un problema ya que va en contra de la suposición básica de la regresión lineal. La presencia de multicolinealidad no afecta la capacidad predictiva del modelo. Entonces, si solo desea predicciones, la presencia de multicolinealidad no afecta su salida. Sin embargo, si desea extraer algunas ideas del modelo y aplicarlas, digamos, en algún modelo comercial, puede causar problemas.
Uno de los principales problemas causados por la multicolinealidad es que conduce a interpretaciones incorrectas y proporciona conocimientos erróneos. Los coeficientes de regresión lineal sugieren el cambio medio en el valor objetivo si una característica cambia en una unidad. Por lo tanto, si existe multicolinealidad, esto no es cierto, ya que cambiar una característica provocará cambios en la variable correlacionada y los consiguientes cambios en la variable de destino. Esto conduce a conocimientos erróneos y puede producir resultados peligrosos para una empresa.
Una forma muy efectiva de lidiar con la multicolinealidad es el uso de VIF (Factor de inflación de varianza). Cuanto mayor sea el valor de VIF para una función, más linealmente correlacionada está esa función. Simplemente elimine la función con un valor de VIF muy alto y vuelva a entrenar el modelo en el conjunto de datos restante.
10. ¿Cuál es la forma normal (ecuación) de la regresión lineal? ¿Cuándo se debe preferir al método de descenso de gradiente?
La ecuación normal para la regresión lineal es:
β=(X T X) -1 . X T Y
Aquí, Y=β T X es el modelo para la regresión lineal,
Y es la variable objetivo o dependiente,
β es el vector del coeficiente de regresión, al que se llega utilizando la ecuación normal,
X es la matriz de características que contiene todas las características como columnas.
Tenga en cuenta aquí que la primera columna en la matriz X consiste en todos los 1. Esto es para incorporar el valor de compensación para la línea de regresión.
Comparación entre gradiente descendente y ecuación normal:
| Descenso de gradiente | ecuación normal |
| Necesita ajuste de hiperparámetros para alfa (parámetro de aprendizaje) | No hay tal necesidad |
| Es un proceso iterativo | Es un proceso no iterativo. |
| O(kn 2 ) complejidad temporal | O(n 3 ) complejidad temporal debido a la evaluación de X T X |
| Preferido cuando n es extremadamente grande | Se vuelve bastante lento para valores grandes de n |
Aquí, ' k ' es el número máximo de iteraciones para el descenso de gradiente y ' n ' es el número total de puntos de datos en el conjunto de entrenamiento.
Claramente, si tenemos grandes datos de entrenamiento, no se prefiere el uso de la ecuación normal. Para valores pequeños de ' n ', la ecuación normal es más rápida que el descenso de gradiente.
Qué es el aprendizaje automático y por qué es importante
11. Ejecutas tu regresión en diferentes subconjuntos de tus datos, y en cada subconjunto, el valor beta para una determinada variable varía enormemente. ¿Cuál podría ser el problema aquí?
Este caso implica que el conjunto de datos es heterogéneo. Entonces, para superar este problema, el conjunto de datos se debe agrupar en diferentes subconjuntos y luego se deben construir modelos separados para cada grupo. Otra forma de lidiar con este problema es usar modelos no paramétricos, como árboles de decisión, que pueden tratar con datos heterogéneos de manera bastante eficiente.

12. Su regresión lineal no se ejecuta y comunica que hay un número infinito de mejores estimaciones para los coeficientes de regresión. ¿Qué podría estar mal?
Esta condición surge cuando existe una correlación perfecta (positiva o negativa) entre algunas variables. En este caso, no hay un valor único para los coeficientes y, por lo tanto, surge la condición dada.
13. ¿Qué quiere decir con R 2 ajustado ? ¿En qué se diferencia de R 2 ?
El R 2 ajustado , al igual que el R 2 , es un representante del número de puntos que se encuentran alrededor de la línea de regresión. Es decir, muestra qué tan bien se ajusta el modelo a los datos de entrenamiento. La fórmula para R 2 ajustado es -
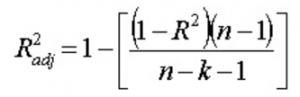
Aquí, n es el número de puntos de datos y k es el número de características.
Un inconveniente de R 2 es que siempre aumentará con la adición de una nueva característica, ya sea que la nueva característica sea útil o no. El R 2 ajustado supera este inconveniente. El valor del R 2 ajustado aumenta solo si la característica recién agregada juega un papel importante en el modelo.
14. ¿Cómo interpreta la curva de valor residual vs valor ajustado?
La gráfica de valor residual frente a valor ajustado se usa para ver si los valores pronosticados y los residuales tienen una correlación o no. Si los residuos se distribuyen normalmente, con una media alrededor del valor ajustado y una varianza constante, nuestro modelo funciona bien; de lo contrario, hay algún problema con el modelo.
El problema más común que se puede encontrar al entrenar el modelo en un amplio rango de un conjunto de datos es la heterocedasticidad (esto se explica en la respuesta a continuación). La presencia de heteroscedasticidad se puede ver fácilmente trazando la curva de valor residual frente a valor ajustado.
15. ¿Qué es la heterocedasticidad? ¿Cuáles son las consecuencias y cómo se puede superar?
Se dice que una variable aleatoria es heteroscedástica cuando diferentes subpoblaciones tienen diferentes variabilidades (desviación estándar).
La existencia de heterocedasticidad da lugar a ciertos problemas en el análisis de regresión, ya que el supuesto dice que los términos de error no están correlacionados y, por lo tanto, la varianza es constante. La presencia de heteroscedasticidad a menudo se puede ver en forma de un gráfico de dispersión en forma de cono para valores residuales frente a valores ajustados.
Uno de los supuestos básicos de la regresión lineal es que la heterocedasticidad no está presente en los datos. Debido a la violación de los supuestos, los estimadores de mínimos cuadrados ordinarios (OLS) no son los mejores estimadores lineales insesgados (BLUE). Por lo tanto, no dan la menor varianza que otros estimadores lineales insesgados (LUEs).
No existe un procedimiento fijo para superar la heterocedasticidad. Sin embargo, hay algunas formas que pueden conducir a una reducción de la heterocedasticidad. Están -
- Logaritmizar los datos: una serie que aumenta exponencialmente a menudo resulta en una mayor variabilidad. Esto se puede superar utilizando la transformación de registro.
- Uso de regresión lineal ponderada: aquí, el método OLS se aplica a los valores ponderados de X e Y. Una forma es asignar pesos directamente relacionados con la magnitud de la variable dependiente.
16. ¿Qué es VIF? ¿Como lo calculas?
El factor de inflación de varianza (VIF) se utiliza para comprobar la presencia de multicolinealidad en un conjunto de datos. Se calcula como—
Aquí, VIF j es el valor de VIF para la j -ésima variable,
R j 2 es el valor de R 2 del modelo cuando se hace una regresión de esa variable contra todas las demás variables independientes.
Si el valor de VIF es alto para una variable, implica que el R 2 el valor del modelo correspondiente es alto, es decir, otras variables independientes son capaces de explicar esa variable. En términos simples, la variable depende linealmente de algunas otras variables.
17. ¿Cómo sabes que la regresión lineal es adecuada para cualquier dato dado?
Para ver si la regresión lineal es adecuada para cualquier dato dado, se puede usar un diagrama de dispersión. Si la relación parece lineal, podemos optar por un modelo lineal. Pero si no es el caso, tenemos que aplicar algunas transformaciones para que la relación sea lineal. Trazar los diagramas de dispersión es fácil en caso de regresión lineal simple o univariada. Pero en el caso de la regresión lineal multivariada, se pueden trazar diagramas de dispersión por pares bidimensionales, diagramas giratorios y gráficos dinámicos.
18. ¿Cómo se usa la prueba de hipótesis en la regresión lineal?
La prueba de hipótesis se puede llevar a cabo en regresión lineal para los siguientes propósitos:
- Para comprobar si un predictor es significativo para la predicción de la variable objetivo. Dos métodos comunes para esto son:
- Mediante el uso de valores de p:
Si el valor p de una variable es mayor que cierto límite (generalmente 0.05), la variable es insignificante en la predicción de la variable objetivo. - Comprobando los valores del coeficiente de regresión:
Si el valor del coeficiente de regresión correspondiente a un predictor es cero, esa variable es insignificante en la predicción de la variable objetivo y no tiene una relación lineal con ella.
- Mediante el uso de valores de p:
- Para comprobar si los coeficientes de regresión calculados son buenos estimadores de los coeficientes reales.
19. Explique el descenso de gradiente con respecto a la regresión lineal.
El descenso de gradiente es un algoritmo de optimización. En regresión lineal, se utiliza para optimizar la función de costo y encontrar los valores de los βs (estimadores) correspondientes al valor optimizado de la función de costo.
El descenso de gradiente funciona como una bola que rueda por un gráfico (ignorando la inercia). La bola se mueve en la dirección del mayor gradiente y se detiene en la superficie plana (mínima). 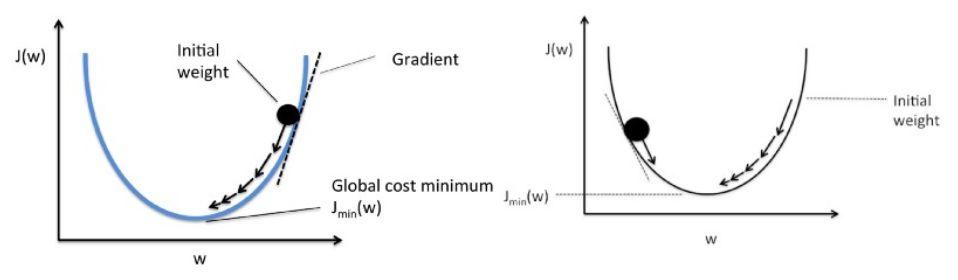
Matemáticamente, el objetivo del descenso de gradiente para la regresión lineal es encontrar la solución de
ArgMin J(Θ 0 ,Θ 1 ), donde J(Θ 0 ,Θ 1 ) es la función de costo de la regresión lineal. Está dado por - 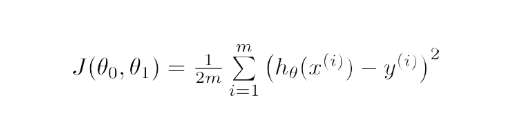
Aquí, h es el modelo de hipótesis lineal, h=Θ 0 + Θ 1 x, y es la salida verdadera y m es el número de puntos de datos en el conjunto de entrenamiento.
Gradient Descent comienza con una solución aleatoria y luego, según la dirección del gradiente, la solución se actualiza al nuevo valor donde la función de costo tiene un valor más bajo.
La actualización es:
Repetir hasta la convergencia 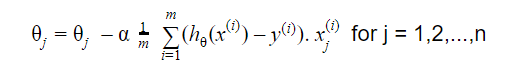
20. ¿Cómo interpretas un modelo de regresión lineal?
Un modelo de regresión lineal es bastante fácil de interpretar. El modelo es de la siguiente forma: 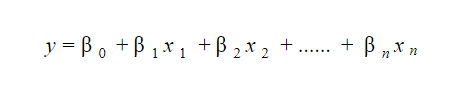
La importancia de este modelo radica en el hecho de que uno puede interpretar y comprender fácilmente los cambios marginales y sus consecuencias. Por ejemplo, si el valor de x 0 aumenta en 1 unidad, manteniendo constantes las demás variables, el aumento total en el valor de y será β i . Matemáticamente, el término de intersección ( β 0 ) es la respuesta cuando todos los términos predictores se establecen en cero o no se consideran.
Estas 6 técnicas de aprendizaje automático están mejorando la atención médica
21. ¿Qué es la regresión robusta?
Un modelo de regresión debe ser robusto por naturaleza. Esto significa que con cambios en algunas observaciones, el modelo no debería cambiar drásticamente. Además, no debería verse muy afectado por los valores atípicos.
Un modelo de regresión con MCO (Mínimos cuadrados ordinarios) es bastante sensible a los valores atípicos. Para superar este problema, podemos utilizar el método WLS (Weighted Least Squares) para determinar los estimadores de los coeficientes de regresión. Aquí, se asignan menos pesos a los valores atípicos o a los puntos de mayor influencia en el ajuste, lo que hace que estos puntos tengan menos impacto.
22. ¿Qué gráficos se sugiere observar antes de ajustar el modelo?
Antes de ajustar el modelo, uno debe ser muy consciente de los datos, como cuáles son las tendencias, la distribución, la asimetría, etc. en las variables. Se pueden usar gráficos como histogramas, diagramas de caja y diagramas de puntos para observar la distribución de las variables. Aparte de esto, también se debe analizar cuál es la relación entre las variables dependientes e independientes. Esto se puede hacer mediante diagramas de dispersión (en el caso de problemas univariados), diagramas rotativos, diagramas dinámicos, etc.
23. ¿Qué es el modelo lineal generalizado?
El modelo lineal generalizado es la derivada del modelo de regresión lineal ordinario. GLM es más flexible en términos de residuos y se puede utilizar cuando la regresión lineal no parece apropiada. GLM permite que la distribución de residuos sea diferente a una distribución normal. Generaliza la regresión lineal al permitir que el modelo lineal se vincule a la variable de destino mediante la función de enlace. La estimación del modelo se realiza utilizando el método de estimación de máxima verosimilitud.
24. Explique el equilibrio entre sesgo y varianza.
El sesgo se refiere a la diferencia entre los valores predichos por el modelo y los valores reales. es un error Uno de los objetivos de un algoritmo ML es tener un sesgo bajo.
La varianza se refiere a la sensibilidad del modelo a pequeñas fluctuaciones en el conjunto de datos de entrenamiento. Otro objetivo de un algoritmo ML es tener una varianza baja.
Para un conjunto de datos que no es exactamente lineal, no es posible tener un sesgo y una varianza bajos al mismo tiempo. Un modelo de línea recta tendrá una varianza baja pero un sesgo alto, mientras que un polinomio de alto grado tendrá un sesgo bajo pero una varianza alta.
No se puede escapar de la relación entre el sesgo y la variación en el aprendizaje automático.
- Disminuir el sesgo aumenta la varianza.
- Disminuir la varianza aumenta el sesgo.
Entonces, hay una compensación entre los dos; el especialista en ML tiene que decidir, en función del problema asignado, cuánto sesgo y varianza se pueden tolerar. En base a esto, se construye el modelo final.
25. ¿Cómo pueden las curvas de aprendizaje ayudar a crear un mejor modelo?
Las curvas de aprendizaje dan la indicación de la presencia de overfitting o underfitting.
En una curva de aprendizaje, el error de entrenamiento y el error de validación cruzada se representan frente al número de puntos de datos de entrenamiento. Una curva de aprendizaje típica se ve así: 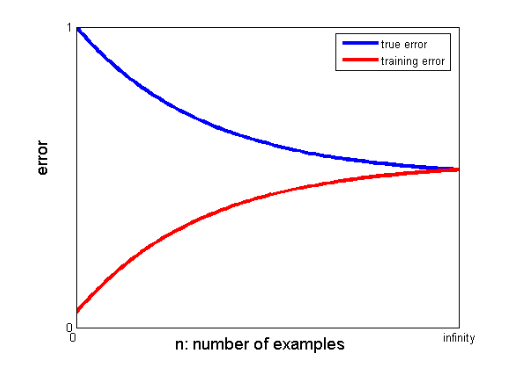
Si el error de entrenamiento y el error verdadero (error de validación cruzada) convergen en el mismo valor y el valor correspondiente del error es alto, indica que el modelo no se ajusta correctamente y sufre un alto sesgo.
Entrevistas de aprendizaje automático y cómo dominarlas
Las entrevistas de aprendizaje automático pueden variar según los tipos o categorías, por ejemplo, algunos reclutadores hacen muchas preguntas de entrevista de regresión lineal . Al optar por el puesto de ingeniero de aprendizaje automático, pueden especializarse en categorías como codificación, investigación, estudio de casos, gestión de proyectos, presentación, diseño de sistemas y estadísticas. Nos centraremos en los tipos de categorías más comunes y cómo prepararse para ellas.
- Codificación
La codificación y la programación son componentes importantes de una entrevista de aprendizaje automático y se utilizan con frecuencia para evaluar a los solicitantes. Para hacerlo bien en estas entrevistas, debe tener sólidas habilidades de programación. Las entrevistas de codificación generalmente duran de 45 a 60 minutos y se componen de solo dos preguntas. El entrevistador plantea el tema y prevé que el aspirante lo abordará en el menor tiempo posible.
Cómo prepararse: puede prepararse para estas entrevistas teniendo una buena comprensión de las estructuras de datos, las complejidades del tiempo y el espacio, las habilidades de gestión y la capacidad de comprender y resolver un problema. upGrad tiene un excelente curso de ingeniería de software que puede ayudarlo a mejorar sus habilidades de codificación y superar esa entrevista.
2. Aprendizaje automático
Su comprensión del aprendizaje automático se evaluará a través de entrevistas. Las capas convolucionales, las redes neuronales recurrentes, las redes adversarias generativas, el reconocimiento de voz y otros temas pueden cubrirse según las necesidades de empleo.
Cómo prepararse: para poder superar esta entrevista, debe asegurarse de tener un conocimiento profundo de las funciones y responsabilidades del trabajo. Esto te ayudará a identificar las especificaciones de ML que debes estudiar. Sin embargo, si no encuentra ninguna especificación, debe comprender profundamente los conceptos básicos. Un curso detallado en ML que proporciona upGrad puede ayudarlo con eso. También puede estudiar los últimos artículos sobre ML e IA para comprender sus últimas tendencias y puede incorporarlos regularmente.
3. Cribado
Esta entrevista es algo informal y suele ser uno de los puntos iniciales de la entrevista. Un posible empleador a menudo se encarga de ello. El objetivo principal de esta entrevista es proporcionar al solicitante una idea del negocio, el rol y los deberes. En un ambiente más informal, también se pregunta al candidato sobre su pasado para determinar si su área de interés coincide con el puesto.
Cómo prepararse: esta es una parte muy poco técnica de la entrevista. Todo esto requerido es tu honestidad y los fundamentos de tu especialización en Machine Learning.
4. Diseño del sistema
Estas entrevistas ponen a prueba la capacidad de una persona para crear una solución totalmente escalable de principio a fin. La mayoría de los ingenieros están tan preocupados por un problema que con frecuencia pasan por alto el panorama general. Una entrevista de diseño de sistema requiere una comprensión de numerosos elementos que se combinan para producir una solución. Estos elementos incluyen el diseño de front-end, el balanceador de carga, el caché y más. Es más fácil desarrollar un sistema de extremo a extremo efectivo y escalable cuando se entienden bien estos problemas.
Cómo prepararse: comprender los conceptos y componentes del proyecto de diseño del sistema. Use ejemplos de la vida real para explicar la estructura a su entrevistador para una mejor comprensión del proyecto.
Blogs populares sobre aprendizaje automático e inteligencia artificial
| IoT: Historia, Presente y Futuro | Tutorial de aprendizaje automático: Aprenda ML | ¿Qué es Algoritmo? Simplemente fácil |
| Salario del ingeniero de robótica en la India: todos los roles | Un día en la vida de un ingeniero de aprendizaje automático: ¿qué hacen? | ¿Qué es IoT (Internet de las Cosas)? |
| Permutación vs Combinación: Diferencia entre Permutación y Combinación | Las 7 principales tendencias en inteligencia artificial y aprendizaje automático | Aprendizaje automático con R: todo lo que necesita saber |

Si hay una brecha significativa entre los valores convergentes de los errores de entrenamiento y validación cruzada, es decir, el error de validación cruzada es significativamente más alto que el error de entrenamiento, sugiere que el modelo se está sobreajustando a los datos de entrenamiento y sufre una gran varianza. .
Ingenieros de aprendizaje automático: mitos frente a realidades
Ese es el final de la primera sección de esta serie. Quédese para la siguiente parte de la serie que consiste en preguntas basadas en la regresión logística . Sientete libre de publicar tus comentarios.
Co-escrito por – Ojas Agarwal
Puede consultar nuestro programa Executive PG en aprendizaje automático e IA , que ofrece talleres prácticos, mentor individual de la industria, 12 estudios de casos y asignaciones, estado de exalumno de IIIT-B y más.
¿Qué entiendes por regularización?
La regularización es una estrategia para tratar el problema del sobreajuste del modelo. El sobreajuste ocurre cuando se aplica un modelo complicado a los datos de entrenamiento. Es posible que el modelo básico no pueda generalizar los datos a veces, y el modelo complicado puede sobreajustar los datos. La regularización se utiliza para paliar este problema. La regularización es el proceso de agregar términos de coeficientes (betas) al problema de minimización de tal manera que los términos se penalicen y tengan una magnitud modesta. Básicamente, esto ayuda a identificar patrones de datos y, al mismo tiempo, evita el sobreajuste al evitar que el modelo se vuelva demasiado complejo.
¿Qué entiendes sobre la ingeniería de funciones?
El proceso de cambiar los datos originales en características que describan mejor el problema subyacente a los modelos predictivos, lo que da como resultado una mayor precisión del modelo en datos no vistos, se conoce como ingeniería de características. En términos sencillos, la ingeniería de características se refiere a la creación de características adicionales que pueden ayudar a comprender y modelar mejor un problema. Hay dos tipos de ingeniería de características: impulsada por el negocio y basada en datos. La incorporación de características desde un punto de vista comercial es el enfoque de la ingeniería de características impulsada por el negocio.
¿Qué es la compensación sesgo-varianza?
La brecha entre el modelo: los valores predichos y los valores reales se denomina sesgo. Es un error. Un sesgo bajo es uno de los objetivos de un algoritmo ML. La vulnerabilidad del modelo a pequeños cambios en el conjunto de datos de entrenamiento se conoce como varianza. La varianza baja es otro objetivo de un algoritmo ML. Es imposible tener tanto un sesgo bajo como una varianza baja en un conjunto de datos que no es perfectamente lineal. La varianza de un modelo de línea recta es baja, pero el sesgo es grande, mientras que la varianza de un polinomio de alto grado es baja, pero el sesgo es alto. En el aprendizaje automático, el vínculo entre el sesgo y la variación es inevitable.
