Introducción a la Función de Densidad de Probabilidad [Fórmula, Propiedades, Aplicaciones, Ejemplos]

La función de densidad de probabilidad (PDF) es una expresión en estadística que denota la distribución de probabilidad de una variable aleatoria discreta. La distribución de probabilidad, en términos simples, se puede definir como la probabilidad de un resultado de una variable aleatoria como una acción o un ETF. Las variables discretas se producen en contraste con una variable aleatoria continua cuyo valor exacto se puede determinar.

Por ejemplo, el valor de los vales en una bolsa de valores tiene solo dos puntos decimales (por ejemplo, 65,76) en una variable aleatoria discreta en lugar de una variable continua con cualquier número de puntos decimales (ejemplo: 65,7685434567).

Una función de densidad de probabilidad es una herramienta estadística utilizada para determinar la probabilidad del resultado de una variable aleatoria discreta. Cuando se representan en un gráfico, las PDF se ven idénticas a una curva de campana en la que el área bajo la curva representa la probabilidad del resultado.

Cuando se proyecta como un modelo gráfico, el área bajo la curva representa el rango en el que caerán los valores de las variables aleatorias discretas. Por lo tanto, el área total bajo la curva es igual a la probabilidad del resultado de la variable.

La función de densidad de probabilidad puede determinar la probabilidad de que una variable aleatoria se encuentre dentro de un rango específico de valores.

Por lo general, las funciones de densidad de probabilidad analizan los riesgos y los ingresos potenciales asociados con un fondo específico en el mercado de valores.

Condiciones que debe satisfacer una función para ser considerada una función de densidad de probabilidad

El valor de una variable discreta se puede medir con precisión en contraste con una variable continua que puede tener un número infinito de valores. Cualquier función debe satisfacer las dos condiciones siguientes para ser una función de densidad de probabilidad:

• El valor de f(x) para cada valor posible de la variable aleatoria debe ser positivo (no negativo).
• El valor integral del área total de la curva (integral de todos los valores posibles de la variable aleatoria) debe ser 1.

Diferencia entre la función de densidad de probabilidad y la función de distribución de probabilidad

Las variables aleatorias pueden tener muchos valores. La descripción de cada valor posible que puede tener una variable aleatoria se denomina distribución de probabilidad.

La distribución de probabilidad da un conjunto de resultados y sus probabilidades relacionadas. La función estadística que representa una distribución de probabilidad continua se conoce como función de densidad de probabilidad.

Hay otra herramienta estadística que representa una distribución de probabilidad discreta llamada función de masa de probabilidad. Esto da una cuenta detallada de todos los resultados posibles y sus probabilidades de verosimilitud.

Expresión para funciones de densidad de probabilidad

Si la variable aleatoria es discreta, su distribución de probabilidad se llama función de masa de probabilidad, y si es una variable continua, la distribución de probabilidad se llama función de densidad de probabilidad.

Se utiliza un PDF cuando la variable aleatoria en cuestión tiene un rango de valores posibles. Su distribución de probabilidad se utiliza para determinar el valor exacto.

Sea X la variable aleatoria. La función de densidad de probabilidad, f de la variable aleatoria X se puede expresar como

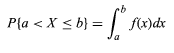
• El valor de la variable aleatoria se encuentra entre a y b.
• Si X denota la probabilidad de seleccionar un número particular del rango (intervalo) r y s, entonces la función de densidad de probabilidad se puede expresar como

f ( x ) = 1/( s - r ) para r < x < s y f ( x ) = 0 para x < r o x > s .

• El PDF F se representa como:

F ( X ) = PAGS { X ≤ X }

que se denomina función de distribución o función de distribución acumulada de X.

Considerando que la variable aleatoria X tiene una función de distribución de probabilidad f ( x ), entonces la relación entre f y F se puede establecer como

F ′(. x ) = f ( x )

La función de distribución de una variable aleatoria discreta es diferente de su función de distribución de probabilidad. La relación entre ambos se puede expresar de la siguiente manera:

La expectativa de la variable aleatoria se denota como,

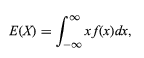
Por lo tanto, todas las variables discretas y aleatorias se pueden tratar de manera uniforme con la ayuda de una teoría combinada.

La fórmula de la función de densidad de probabilidad

La probabilidad de una variable aleatoria continua X en algún valor fijo x siempre es 0. En este caso, no se puede usar P(X = x). Debe determinarse el valor de X que se encuentra entre un rango de valores (a,b). Para determinar la misma se utiliza la siguiente fórmula.

Propiedades de una función de densidad de probabilidad

Una variable aleatoria continua que toma su valor entre el rango (a,b), por ejemplo, se estimará calculando el área bajo la curva y el eje X trazado con (a) como su límite inferior y (b) como su limite superior. La función de densidad de probabilidad para lo anterior se representa como:

La función de densidad de probabilidad es positiva (no negativa) para todos los valores posibles. Esto significa f(x)≥ 0, para cada x. El área que cae entre la curva de densidad y el eje X (eje horizontal) es igual a 1.

Esto también se puede denotar como:

La curva de la función de densidad es continua en todo el rango dado, que está claramente definido contra una serie de valores continuos o el dominio de la variable.

Únase al curso de aprendizaje automático en línea de las mejores universidades del mundo: maestrías, programas ejecutivos de posgrado y programa de certificado avanzado en ML e IA para acelerar su carrera.

Aplicaciones de la función de densidad de probabilidad

• La función de densidad de probabilidad se utiliza en el modelado anual de los niveles de concentración de NO atmosférico.
• Modelización de la combustión de motores diesel.
• En estadística, la función de densidad de probabilidad se utiliza para determinar las posibilidades del resultado de una variable aleatoria.

Ejemplos de función de densidad de probabilidad

• Ejemplo 1

A continuación se muestra un ejemplo de cómo se utiliza la función de densidad de probabilidad (PDF) para determinar el potencial de riesgo de un inversor en el mercado de valores:

Primero, los PDF se generan como una herramienta gráfica basada en información histórica.

La forma más común de PDF es la proyección neutral, donde el riesgo es igual a la recompensa en un rango de posibilidades. Los inversores con menos capacidad para asumir riesgos solo serán recompensados ​​con ganancias limitadas y, por lo tanto, se encuentran en el lado izquierdo de la curva de campana. Por el contrario, es probable que los inversores con gran capacidad para asumir riesgos sean recompensados ​​con mayores rendimientos y, por lo tanto, se encuentren en el lado derecho de la curva.

La mayoría de los inversores caen por debajo de la capacidad de asunción de riesgos promedio y, por lo tanto, ocupan la mitad de la curva.

Esto ayuda a analizar la categoría de inversores en función de los datos recibidos. Esto ayuda a los corredores de bolsa a identificar su categoría de clientes objetivo para vender sus productos.

• Ejemplo 2

Una de las aplicaciones esenciales de la función de densidad de probabilidad es la variable aleatoria gaussiana, también conocida como variable aleatoria normal.

En ambos casos, el gráfico da una curva de campana para la función de densidad de probabilidad.

La densidad se puede expresar como

El gráfico de la ecuación de densidad anterior se muestra a continuación.

El área bajo la curva representa el valor real de la variable aleatoria gaussiana.

Conclusión

La función de densidad de probabilidad juega un papel vital en el aprendizaje automático. Para los estudiantes que buscan una carrera en aprendizaje automático e inteligencia artificial, recomendamos inscribirse en el programa de certificado avanzado IIT en aprendizaje automático de upGrad . El programa está personalizado y diseñado para equipar a profesionales de alto nivel para implementar modelos de aprendizaje automático utilizando tecnología de computación en la nube.

El plan de estudios está diseñado por profesores de IIT Madras y expertos de la industria para que el proceso de aprendizaje sea más relevante y práctico. El programa ofrece una certificación reconocida a nivel mundial de la codiciada y número 1 de la universidad de ingeniería en India y apoyo de colocación de 360 ​​grados de upGrad.

Además, obtiene numerosas oportunidades para colaborar en proyectos a gran escala con la base de estudiantes pagados de upGrad de más de 40,000.

¡Dirígete a nuestro sitio web para comenzar tu viaje de aprendizaje!