Introducción a la regresión multivariante en el aprendizaje automático: guía completa

No es ningún secreto que la tecnología actual está basada en datos. Los datos pueden ser solo una compilación de cifras, pero se pueden procesar de manera significativa para extraer productividad e ingenio para que las empresas sigan siendo competitivas y sostenibles a largo plazo. Da la casualidad de que el análisis de datos es la respuesta para obtener estimaciones precisas a partir de información sin procesar.

El análisis de datos es una técnica que involucra ideas estadísticas y lógicas para examinar, procesar y transformar los datos en una forma utilizable. Las soluciones extraídas del análisis de datos se utilizan en las empresas para tomar decisiones vitales. La ciencia de datos junto con el análisis de datos se utiliza para predecir resultados futuros con alta precisión. Es un proceso de empleo de técnicas científicas y algoritmos para obtener información viable de un grupo de datos.

Un problema común al que se enfrentan los profesionales de datos es la manera de determinar si existe una relación estadística entre una variable de respuesta (indicada por Y) y las variables explicativas (indicada por Xi).

La respuesta a esta preocupación es el análisis de regresión. Entendamos esto con más detalle.

¿Qué es el análisis de regresión?

El análisis de regresión es uno de los métodos populares en el análisis de datos que sigue un algoritmo de aprendizaje automático controlado o supervisado. Es una técnica efectiva para identificar y establecer una relación entre variables en los datos.

El análisis de regresión implica clasificar variables viables utilizando estrategias matemáticas para sacar conclusiones muy precisas sobre esas variables ordenadas.

¿Qué es la regresión multivariante?

Multivariante es un algoritmo de aprendizaje automático controlado o supervisado que analiza múltiples variables de datos. Es una continuación de la regresión múltiple que involucra una variable dependiente y muchas variables independientes. La salida se predice en función del número de variables independientes.

La regresión multivariada encuentra una fórmula que explica la respuesta simultánea de los factores presentes en las variables a los cambios en otras. Se utilizan para estudiar los datos en varios campos. Por ejemplo, en bienes raíces, la regresión multivariada se usa para predecir el precio de una casa en función de varios factores, como su ubicación, la cantidad de habitaciones y las comodidades disponibles.

Función de costo en regresión multivariante

La función de costo asigna un costo a las muestras cuando el resultado de un modelo se desvía de los datos observados. La ecuación de la función de costo es el total del cuadrado de la diferencia entre el valor predicho y el valor real dividido por dos veces la longitud del conjunto de datos.

Aquí hay un ejemplo :

resultado :

Fuente

¿Cómo utilizar el análisis de regresión multivariado?

Los procesos involucrados en el análisis de regresión multivariable incluyen la selección de características, la ingeniería de características, la normalización de características, las funciones de pérdida de selección, el análisis de hipótesis y la creación de un modelo de regresión.

1. Selección de características: Es el paso más importante en la regresión multivariada. También conocido como selección de variables, este proceso implica seleccionar variables viables para construir modelos eficientes.
2. Normalización de características: esto implica escalar características para mantener una distribución optimizada y proporciones de datos. Esto ayuda a un mejor análisis de datos. El valor de todas las características se puede cambiar según el requisito.
3. Selección de función de pérdida e hipótesis : La función de pérdida se utiliza para predecir errores. La función de pérdida entra en juego cuando la predicción de la hipótesis cambia de las cifras reales. Aquí, la hipótesis representa el valor predicho de la característica o variable.
4. Fijación del parámetro de hipótesis : el parámetro de la hipótesis se fija o establece de tal manera que minimiza la función de pérdida y mejora la predicción.
5. Reducción de la función de pérdida : la función de pérdida se minimiza generando un algoritmo específico para la minimización de pérdida en el conjunto de datos que, a su vez, facilita la alteración de los parámetros de la hipótesis. El descenso de gradiente es el algoritmo más utilizado para la minimización de pérdidas. El algoritmo también se puede utilizar para otras acciones una vez que se completa la minimización de pérdidas.
6. Analizando la función de la hipótesis : La función de la hipótesis necesita ser analizada ya que es crucial para predecir los valores. Después de analizar la función, se prueba con datos de prueba.

Veamos ahora las dos formas en que se puede usar la regresión multivariada.

1. Regresión lineal multivariante

La regresión lineal multivariante se asemeja a la regresión lineal simple, excepto que en la regresión lineal multivariante, múltiples variables independientes contribuyen a las variables dependientes y, por lo tanto, se utilizan múltiples coeficientes en el cálculo.

• Se utiliza para derivar una relación matemática entre múltiples variables aleatorias. Explica cuántas variables independientes múltiples están asociadas con una variable dependiente.
• Los detalles de las múltiples variables independientes se utilizan para hacer una predicción precisa de la influencia que tienen en la variable de resultado.
• El modelo de regresión lineal multivariante genera una relación en forma lineal (una forma de línea recta) con la mejor aproximación de cada punto de datos.
• La ecuación del modelo de regresión lineal multivariante es:

yi​=β0​+β1​xi1​+β2​xi2​+…+βp​xip​+

donde para i=n observaciones:

Fuente

¿Cuándo se puede usar la regresión lineal?

El modelo de regresión lineal se puede usar solo cuando hay dos variables continuas de las cuales una es dependiente y la otra es independiente.

La variable independiente se utiliza como parámetro para determinar el valor o resultado de la variable dependiente.

2. Regresión logística multivariante

La regresión logística es un algoritmo utilizado para predecir un resultado binario basado en múltiples variables independientes. Un resultado binario tiene dos posibilidades, el escenario sucede (representado por 1) o no sucede (indicado por 0).

La regresión logística se utiliza cuando se trabaja con datos binarios, los datos en los que el resultado (o la variable dependiente) es dicotómico.

¿Dónde se puede utilizar la regresión logística?

La regresión logística se utiliza principalmente para tratar problemas de clasificación. Por ejemplo, para determinar si un correo electrónico es spam o no y si una transacción en particular es maliciosa o no. En el análisis de datos, se utiliza para tomar decisiones calculadas para minimizar las pérdidas y aumentar las ganancias.

La regresión logística multivariante se usa cuando hay una variable dependiente y múltiples resultados. Se diferencia de la regresión logística en que tiene más de dos resultados posibles.

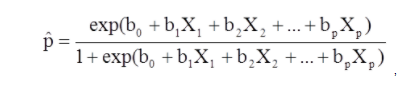
X1 a Xp son variables independientes distintas.

b0 a bp son los coeficientes de regresión

El modelo de regresión logística múltiple también se puede escribir en una forma diferente. En el siguiente formulario, el resultado es el logaritmo esperado de las probabilidades de que el resultado esté presente,

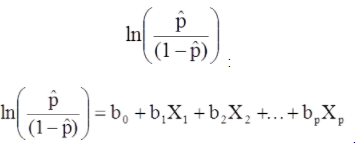
El modelo de regresión logística múltiple también se puede escribir en una forma diferente. En el siguiente formulario, el resultado es el logaritmo esperado de las probabilidades de que el resultado esté presente.

El lado derecho de la ecuación anterior se parece a la ecuación de regresión lineal, pero el método para averiguar los coeficientes de regresión difiere.

Supuestos en el modelo de regresión multivariado

• Las variables dependientes e independientes tienen una relación lineal.
• Las variables independientes no tienen una fuerte correlación entre sí.
• Las observaciones de yi​ se eligen al azar e individualmente de la población.

Supuestos en el modelo de regresión logística multivariante

• La variable dependiente es nominal u ordinal. Las variables nominales tienen dos o más categorías sin ninguna organización significativa. Las variables ordinales también pueden tener dos o más categorías, pero tienen una estructura y se pueden clasificar.
• Puede haber variables independientes únicas o múltiples que pueden ser ordinales, continuas o nominales. Las variables continuas son aquellas que pueden tener infinitos valores dentro de un rango específico.
• Las variables dependientes son mutuamente excluyentes y exhaustivas.
• Las variables independientes no tienen una fuerte correlación entre sí.

Ventajas de la regresión multivariada

1. La regresión multivariante nos ayuda a estudiar las relaciones entre múltiples variables en el conjunto de datos.
2. La correlación entre las variables dependientes e independientes ayuda a predecir el resultado.
3. Es uno de los algoritmos más convenientes y populares utilizados en el aprendizaje automático.

Desventajas de la regresión multivariada

• La complejidad de las técnicas multivariadas requiere cálculos matemáticos complejos.
• No es fácil interpretar el resultado del modelo de regresión multivariable ya que existen inconsistencias en los resultados de pérdida y error.
• Los modelos de regresión multivariable no se pueden aplicar a conjuntos de datos más pequeños; están diseñados para producir resultados precisos cuando se trata de conjuntos de datos más grandes.

Si desea obtener más información sobre la regresión multivariante y otros temas complejos de ciencia de datos, upGrad tiene la solución para usted. Nuestro curso de Maestría en Ciencias en Ciencia de Datos de 18 meses de la Universidad John Moores de Liverpool cubre más de 500 horas de aprendizaje riguroso, 25 sesiones de entrenamiento (realizadas en una base de 1:8) y más de 20 sesiones en vivo. upGrad también ofrece asistencia docente 1:1 y apoyo de orientación profesional de 360° para que los estudiantes transformen sus carreras. Los estudiantes pueden aprovechar el aprendizaje entre pares en la plataforma global con más de 40 000 estudiantes pagos y trabajar en proyectos colaborativos en seis especializaciones funcionales para maximizar su experiencia de aprendizaje.