Gaussian Naive Bayes: ¿Qué necesita saber?
Publicado: 2021-02-22Tabla de contenido
Bayesiano ingenuo gaussiano
Naive Bayes es un algoritmo de aprendizaje automático probabilístico que se utiliza para muchas funciones de clasificación y se basa en el teorema de Bayes. Gaussian Naive Bayes es la extensión de Naive Bayes. Si bien se utilizan otras funciones para estimar la distribución de datos, la distribución gaussiana o normal es la más sencilla de implementar, ya que necesitará calcular la media y la desviación estándar de los datos de entrenamiento.
¿Qué es el Algoritmo Naive Bayes?
Naive Bayes es un algoritmo de aprendizaje automático probabilístico que se puede utilizar en varias tareas de clasificación. Las aplicaciones típicas de Naive Bayes son la clasificación de documentos, el filtrado de spam, la predicción, etc. Este algoritmo se basa en los descubrimientos de Thomas Bayes y de ahí su nombre.
El nombre "Ingenuo" se usa porque el algoritmo incorpora características en su modelo que son independientes entre sí. Cualquier modificación en el valor de una característica no afecta directamente el valor de ninguna otra característica del algoritmo. La principal ventaja del algoritmo Naive Bayes es que es un algoritmo simple pero poderoso.
Se basa en el modelo probabilístico en el que el algoritmo se puede codificar fácilmente y las predicciones se realizan rápidamente en tiempo real. Por lo tanto, este algoritmo es la opción típica para resolver problemas del mundo real, ya que puede ajustarse para responder instantáneamente a las solicitudes de los usuarios. Pero antes de profundizar en Naive Bayes y Gaussian Naive Bayes, debemos saber qué se entiende por probabilidad condicional.
Explicación de la probabilidad condicional
Podemos entender mejor la probabilidad condicional con un ejemplo. Cuando lanzas una moneda, la probabilidad de salir adelante o cruz es del 50%. De manera similar, la probabilidad de obtener un 4 cuando lanzas dados con caras es 1/6 o 0.16.
Si tomamos una baraja de cartas, ¿cuál es la probabilidad de obtener una reina con la condición de que sea una espada? Dado que la condición ya está establecida de que debe ser una espada, el denominador o el conjunto de selección se convierte en 13. Solo hay una reina en espadas, por lo tanto, la probabilidad de elegir una reina de espadas se convierte en 1/13 = 0,07.

La probabilidad condicional de que ocurra el evento A dado el evento B significa la probabilidad de que ocurra el evento A dado que el evento B ya ha ocurrido. Matemáticamente, la probabilidad condicional de A dado B se puede denotar como P[A|B] = P[A AND B] / P[B].
Consideremos un ejemplo un poco complejo. Tome una escuela con un total de 100 estudiantes. Esta población se puede demarcar en 4 categorías: estudiantes, maestros, hombres y mujeres. Considere la tabulación dada a continuación:
| Mujer | Masculino | Total | |
| Profesor | 8 | 12 | 20 |
| Estudiante | 32 | 48 | 80 |
| Total | 40 | 50 | 100 |
Aquí, ¿cuál es la probabilidad condicional de que cierto residente de la escuela sea un maestro dada la condición de que sea un hombre?
Para calcular esto, tendrá que filtrar la subpoblación de 60 hombres y profundizar hasta los 12 profesores varones.
Entonces, la probabilidad condicional esperada P[Profesor | Hombre] = 12/60 = 0,2
P (Profesor | Hombre) = P (Profesor ∩ Hombre) / P (Hombre) = 12/60 = 0,2
Esto se puede representar como un maestro (A) y un hombre (B) dividido por un hombre (B). De manera similar, también se puede calcular la probabilidad condicional de B dado A. La regla que usamos para Naive Bayes se puede concluir a partir de las siguientes notaciones:
PAG (A | B) = PAG (A ∩ B) / PAG (B)
PAG (B | A) = PAG (A ∩ B) / PAG (A)
La regla de Bayes
En la regla de Bayes, vamos de P (X | Y) que se puede encontrar en el conjunto de datos de entrenamiento para encontrar P (Y | X). Para lograr esto, todo lo que necesita hacer es reemplazar A y B con X e Y en las fórmulas anteriores. Para las observaciones, X sería la variable conocida e Y sería la variable desconocida. Para cada fila del conjunto de datos, debe calcular la probabilidad de Y dado que X ya ocurrió.
Pero, ¿qué sucede cuando hay más de 2 categorías en Y? Debemos calcular la probabilidad de cada clase Y para encontrar la ganadora.
A través de la regla de Bayes, vamos de P (X | Y) para encontrar P (Y | X)
Conocido a partir de los datos de entrenamiento: P (X | Y) = P (X ∩ Y) / P(Y)
P (Evidencia | Resultado)
Desconocido – por predecir para datos de prueba: P (Y | X) = P (X ∩ Y) / P(X)

P (Resultado | Evidencia)
Regla de Bayes = P (Y | X) = P (X | Y) * P (Y) / P (X)
Los bayes ingenuos
La regla de Bayes proporciona la fórmula para la probabilidad de Y dada la condición X. Pero en el mundo real, puede haber múltiples variables X. Cuando tiene características independientes, la regla de Bayes se puede extender a la regla de Naive Bayes. Las X son independientes entre sí. La fórmula de Naive Bayes es más poderosa que la fórmula de Bayes
Bayesiano ingenuo gaussiano
Hasta ahora, hemos visto que las X están en categorías, pero ¿cómo calcular las probabilidades cuando X es una variable continua? Si asumimos que X sigue una distribución particular, puede usar la función de densidad de probabilidad de esa distribución para calcular la probabilidad de probabilidades.
Si asumimos que las X siguen una distribución gaussiana o normal, debemos sustituir la densidad de probabilidad de la distribución normal y llamarla bayesiana ingenua gaussiana. Para calcular esta fórmula, necesita la media y la varianza de X.
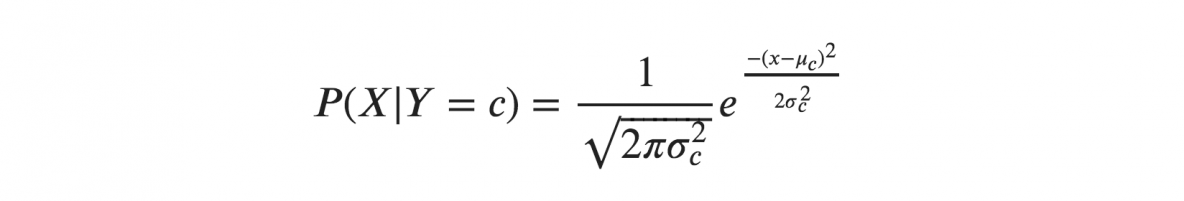
En las fórmulas anteriores, sigma y mu es la varianza y la media de la variable continua X calculada para una clase dada c de Y.
Representación para Gaussian Naive Bayes
La fórmula anterior calculó las probabilidades de los valores de entrada para cada clase a través de una frecuencia. Podemos calcular la media y la desviación estándar de x para cada clase para toda la distribución.
Esto significa que, junto con las probabilidades de cada clase, también debemos almacenar la media y la desviación estándar de cada variable de entrada de la clase.
media(x) = 1/n * suma(x)
donde n representa el número de instancias y x es el valor de la variable de entrada en los datos.
desviación estándar (x) = sqrt (1/n * sum (xi-mean (x) ^ 2))
Aquí se calcula la raíz cuadrada del promedio de las diferencias de cada x y la media de x, donde n es el número de instancias, sum() es la función de suma, sqrt() es la función de raíz cuadrada y xi es un valor específico de x .

Predicciones con el modelo Gaussian Naive Bayes
La función de densidad de probabilidad gaussiana se puede utilizar para hacer predicciones sustituyendo los parámetros con el nuevo valor de entrada de la variable y, como resultado, la función gaussiana dará una estimación de la probabilidad del nuevo valor de entrada.
Clasificador bayesiano ingenuo
El clasificador Naive Bayes asume que el valor de una característica es independiente del valor de cualquier otra característica. Los clasificadores Naive Bayes necesitan datos de entrenamiento para estimar los parámetros necesarios para la clasificación. Debido a su diseño y aplicación simples, los clasificadores Naive Bayes pueden ser adecuados en muchos escenarios de la vida real.
Conclusión
El clasificador Gaussian Naive Bayes es una técnica clasificadora rápida y sencilla que funciona muy bien sin demasiado esfuerzo y con un buen nivel de precisión.
Si está interesado en obtener más información sobre IA, aprendizaje automático, consulte el Diploma PG de IIIT-B y upGrad en Aprendizaje automático e IA, que está diseñado para profesionales que trabajan y ofrece más de 450 horas de capacitación rigurosa, más de 30 estudios de casos y asignaciones, Estado de ex alumnos de IIIT-B, más de 5 proyectos prácticos finales y asistencia laboral con las mejores empresas.
Aprenda el curso ML de las mejores universidades del mundo. Obtenga programas de maestría, PGP ejecutivo o certificado avanzado para acelerar su carrera.
¿Qué es un algoritmo bayesiano ingenuo?
Naive bayes es un algoritmo clásico de aprendizaje automático. Teniendo su origen en las estadísticas, Naive Bayes es un algoritmo simple y poderoso. Naive bayes es una familia de clasificadores basados en la aplicación de un análisis de probabilidad condicional. En este análisis, la probabilidad condicional de un evento se calcula utilizando la probabilidad de cada uno de los eventos individuales que constituyen el evento. Los clasificadores Naive Bayes a menudo se encuentran extremadamente efectivos en la práctica, especialmente cuando el número de dimensiones del conjunto de características es grande.
¿Cuáles son las aplicaciones del algoritmo naive bayes?
Naive Bayes se utiliza en la clasificación de texto, clasificación de documentos y para la indexación de documentos. En naive bayes, cada característica posible no tiene ningún peso asignado en la fase de preprocesamiento y los pesos se asignan más tarde durante las fases de entrenamiento y reconocimiento. La suposición básica del algoritmo bayesiano ingenuo es que las características son independientes.
¿Qué es el algoritmo Gaussian Naive Bayes?
Gaussian Naive Bayes es un algoritmo de clasificación probabilística basado en la aplicación del teorema de Bayes con fuertes suposiciones de independencia. En el contexto de la clasificación, la independencia se refiere a la idea de que la presencia de un valor de una característica no influye en la presencia de otro (a diferencia de la independencia en la teoría de la probabilidad). Ingenuo se refiere al uso de la suposición de que las características de un objeto son independientes entre sí. En el contexto del aprendizaje automático, se sabe que los clasificadores de Bayes ingenuos son muy expresivos, escalables y razonablemente precisos, pero su rendimiento se deteriora rápidamente con el crecimiento del conjunto de entrenamiento. Una serie de características contribuyen al éxito de los clasificadores naive Bayes. En particular, no requieren ningún ajuste de los parámetros del modelo de clasificación, se escalan bien con el tamaño del conjunto de datos de entrenamiento y pueden manejar fácilmente características continuas.
