Encontrar el tercer número más pequeño en Java: una guía completa

¿Alguna vez te has preguntado cómo encontrar eficientemente el tercer número más pequeño en una matriz, lista o secuencia de números enteros? En esta publicación de blog, nos sumergiremos en el mundo de la programación Java y exploraremos diferentes técnicas para identificar el tercer número más pequeño en varias fuentes de datos.

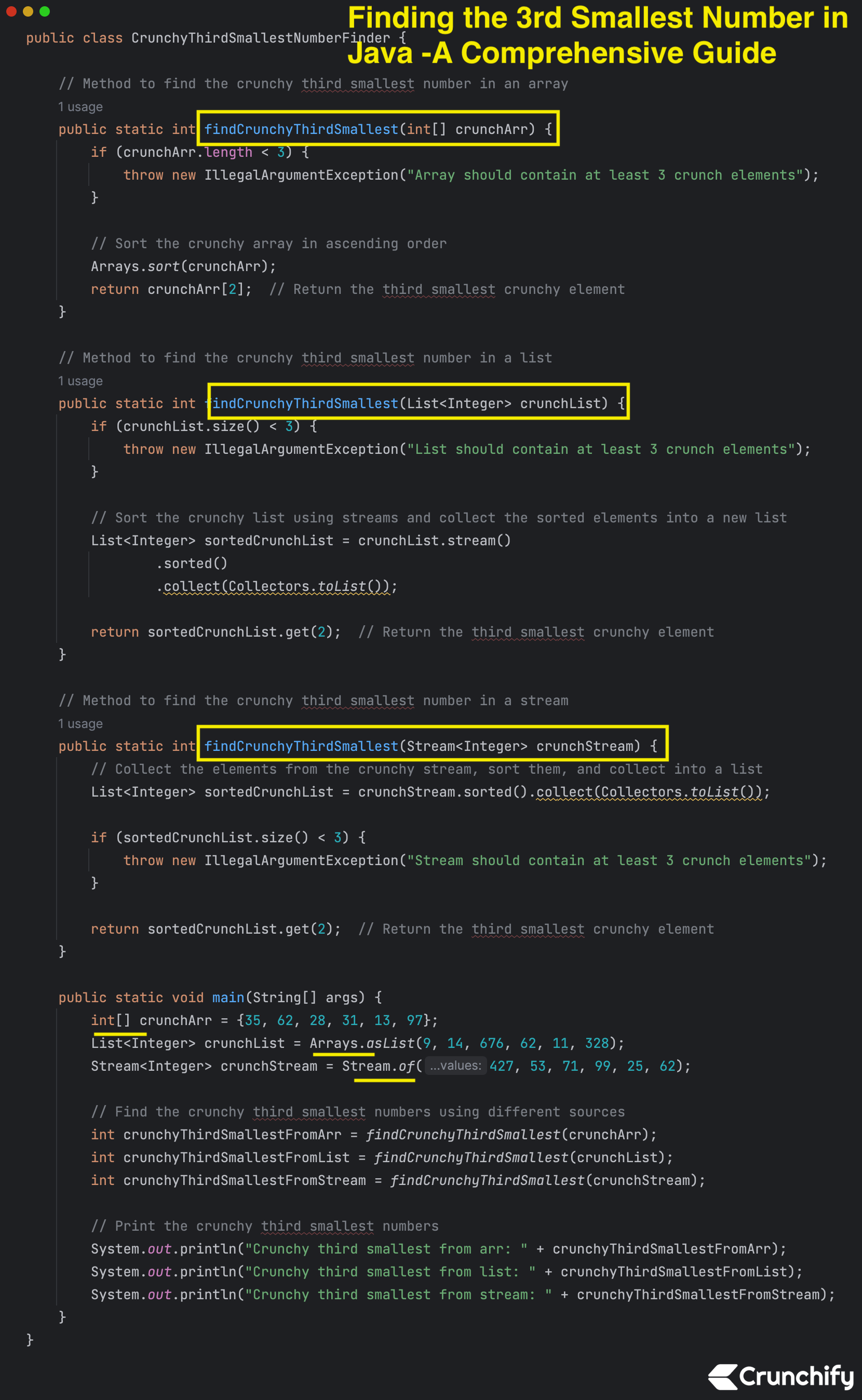
Cuando se trabaja con manipulación y análisis de datos, a menudo surge la necesidad de identificar elementos específicos dentro de una colección de números. Encontrar el número más pequeño o más grande es relativamente sencillo, pero determinar el tercer número más pequeño requiere un poco más de delicadeza. En esta publicación de blog, cubriremos tres métodos para abordar este problema usando Java: ordenar una matriz, ordenar una lista y utilizar secuencias.

Método 1: ordenar una matriz

Las matrices son una de las estructuras de datos fundamentales en Java, lo que las convierte en un punto de partida natural para nuestra exploración. La idea aquí es ordenar la matriz en orden ascendente y luego recuperar el elemento en el índice 2.

Método 2: ordenar una lista

Las listas proporcionan una alternativa más flexible a las matrices, ya que permiten un cambio de tamaño dinámico y una manipulación más sencilla. Para encontrar el tercer número más pequeño en una lista, podemos seguir un enfoque similar a la clasificación de matrices.

Método 3: utilizar transmisiones

Los flujos de Java son una forma poderosa de procesar secuencias de elementos. Podemos usar secuencias para ordenar los elementos y luego recuperar el tercer número más pequeño.

Elegir el método correcto

Cada método tiene sus propias ventajas y casos de uso. Si tiene una matriz a mano, el método de clasificación de matrices podría ser el más eficiente. Las listas son versátiles y ofrecen más comodidad, mientras que las secuencias proporcionan un enfoque funcional y pueden manejar conjuntos de datos más grandes con facilidad.

Aquí tienes un ejemplo completo:

CrunchyThirdSmallestNumberFinder.java

 paquete crunchify.com.tutorial;

importar java.util.Arrays;
importar java.util.List;
importar java.util.stream.Collectors;
importar java.util.stream.Stream;

/**
 * @autor Crunchify.com
 * Encontrar el tercer número más pequeño en Java: una guía completa
 *
 */

clase pública CrunchyThirdSmallestNumberFinder {

    // Método para encontrar el tercer número más pequeño de una matriz
    público estático int findCrunchyThirdSmallest(int[] crunchArr) {
        si (crunchArr.length <3) {
            throw new IllegalArgumentException("La matriz debe contener al menos 3 elementos crujientes");
        }

        // Ordena la matriz crujiente en orden ascendente
        Arrays.sort(crunchArr);
        devolver crunchArr[2]; // Devuelve el tercer elemento crujiente más pequeño
    }

    // Método para encontrar el tercer número más pequeño de una lista
    public static int findCrunchyThirdSmallest(List<Integer> crunchList) {
        si (crunchList.size() < 3) {
            throw new IllegalArgumentException("La lista debe contener al menos 3 elementos cruciales");
        }

        // Ordena la lista crujiente usando secuencias y recopila los elementos ordenados en una nueva lista
        Lista<Entero> ordenadoCrunchList = crunchList.stream()
                .ordenado()
                .collect(Collectors.toList());

        devolver ordenadoCrunchList.get(2); // Devuelve el tercer elemento crujiente más pequeño
    }

    // Método para encontrar el tercer número más pequeño de una secuencia
    public static int findCrunchyThirdSmallest(Stream<Integer> crunchStream) {
        // Recopila los elementos del flujo crujiente, los ordena y los reúne en una lista
        Lista<Integer> sortedCrunchList = crunchStream.sorted().collect(Collectors.toList());

        si (sortedCrunchList.size() < 3) {
            throw new IllegalArgumentException("La secuencia debe contener al menos 3 elementos cruciales");
        }

        devolver ordenadoCrunchList.get(2); // Devuelve el tercer elemento crujiente más pequeño
    }

    público estático vacío principal (String [] argumentos) {
        int[] crunchArr = {35, 62, 28, 31, 13, 97};
        Lista<Integer> crunchList = Arrays.asList(9, 14, 676, 62, 11, 328);
        Stream<Integer> crunchStream = Stream.of(427, 53, 71, 99, 25, 62);

        // Encuentra el tercer número más pequeño utilizando diferentes fuentes
        int crujienteThirdSmallestFromArr = findCrunchyThirdSmallest(crunchArr);
        int crunchyThirdSmallestFromList = encontrarCrunchyThirdSmallest(crunchList);
        int crujienteThirdSmallestFromStream = findCrunchyThirdSmallest(crunchStream);

        // Imprime los terceros números más pequeños crujientes
        System.out.println("Crunchy tercero más pequeño de arr: " + crunchyThirdSmallestFromArr);
        System.out.println("Crunchy tercero más pequeño de la lista: " + crunchyThirdSmallestFromList);
        System.out.println("Crunchy tercero más pequeño de la secuencia: " + crunchyThirdSmallestFromStream);
    }
}

Resultado de la consola Eclipse:

Simplemente ejecute el programa anterior en Eclipse IDE o IntelliJ IDEA y obtendrá el siguiente resultado.

 Crujiente tercero más pequeño del arr: 31
Crujiente tercero más pequeño de la lista: 14
Crujiente tercero más pequeño de la corriente: 62

Proceso finalizado con código de salida 0

Hay algunas diferencias de rendimiento a considerar:

En términos de complejidad temporal, los tres métodos tienen pasos de clasificación similares, que generalmente tienen una complejidad temporal de O(n log n) , donde 'n' es el número de elementos de la colección (matriz, lista o secuencia).

La complejidad temporal de acceder al tercer elemento más pequeño es constante, O(1) , ya que es una búsqueda simple de matriz o lista.

1. Método de matriz: este método ordena la matriz en su lugar, por lo que no requiere memoria adicional para una nueva colección ordenada. Esto puede conducir a un uso de memoria ligeramente mejor en comparación con los métodos de lista y transmisión.
2. Método de lista: este método convierte la lista en una lista ordenada mediante secuencias. Si bien es conveniente, implica crear una nueva lista, lo que consume memoria adicional. Esto puede ser una preocupación si el uso de la memoria es crucial.
3. Método de transmisión: el método de transmisión es bastante flexible y funcional, pero implica recopilar la transmisión en una lista. Esto agrega una pequeña sobrecarga en términos de memoria y procesamiento en comparación con la clasificación directa de la matriz.

Avíseme si tiene algún problema al ejecutar este código.