Diferentes tipos de modelos de regresión que necesita saber

Los problemas de regresión son comunes en el aprendizaje automático y la técnica más común para resolverlos es el análisis de regresión. Se basa en el modelado de datos e implica calcular la línea de mejor ajuste, que pasa por todos los puntos de datos para que la distancia entre la línea y cada punto de datos sea mínima. Si bien existen muchas técnicas diferentes de análisis de regresión, la regresión lineal y logística son las más destacadas. El tipo de modelo de análisis de regresión que usemos eventualmente dependerá de la naturaleza de los datos involucrados.

Averigüemos más sobre el análisis de regresión y los diferentes tipos de modelos de análisis de regresión.

¿Qué es el análisis de regresión?

El análisis de regresión es una técnica de modelado predictivo para determinar la relación entre las variables dependientes (objetivo) y las variables independientes en un conjunto de datos. Por lo general, se usa cuando la variable objetivo contiene valores continuos y las variables dependientes e independientes comparten una relación lineal o no lineal. Por lo tanto, las técnicas de análisis de regresión encuentran uso para determinar la relación de efecto causal entre variables, modelos de series de tiempo y pronósticos. Por ejemplo, la relación entre las ventas y los gastos de publicidad de una empresa se puede estudiar mejor mediante un análisis de regresión.

Tipos de análisis de regresión

Hay muchos tipos diferentes de técnicas de análisis de regresión que podemos usar para hacer predicciones. Además, el uso de cada técnica depende de factores como el número de variables independientes, la forma de la línea de regresión y el tipo de variable dependiente.

Comprendamos algunos de los métodos de análisis de regresión más utilizados:

1. Regresión lineal

La regresión lineal es la técnica de modelado más conocida y asume una relación lineal entre una variable dependiente (Y) y una variable independiente (X). Establece esta relación lineal utilizando una línea de regresión, también conocida como línea de mejor ajuste. La relación lineal está representada por la ecuación Y = c+m*X + e, donde 'c' es la intersección, 'm' es la pendiente de la línea y 'e' es el término de error.

El modelo de regresión lineal puede ser simple (con una variable dependiente y una independiente) o múltiple (con una variable dependiente y más de una variable independiente).

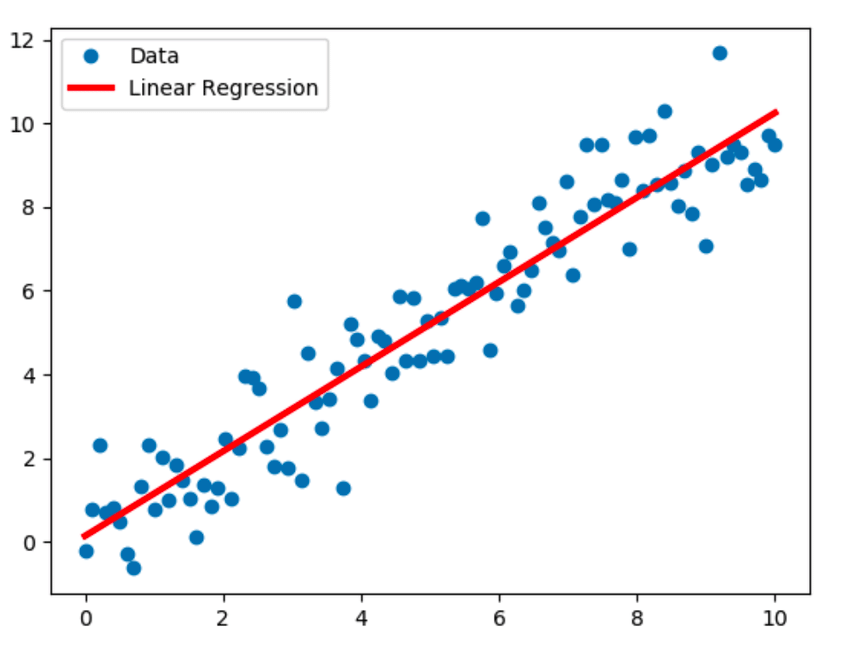
Fuente

2. Regresión logística

La técnica de análisis de regresión logística encuentra uso cuando la variable dependiente es discreta. En otras palabras, esta técnica se usa para estimar la probabilidad de eventos mutuamente excluyentes como pasa/falla, verdadero/falso, 0/1, etc. Por lo tanto, la variable objetivo puede tener solo uno de dos valores, y una curva sigmoidea representa su relación con la variable independiente. El valor de la probabilidad oscila entre 0 y 1.

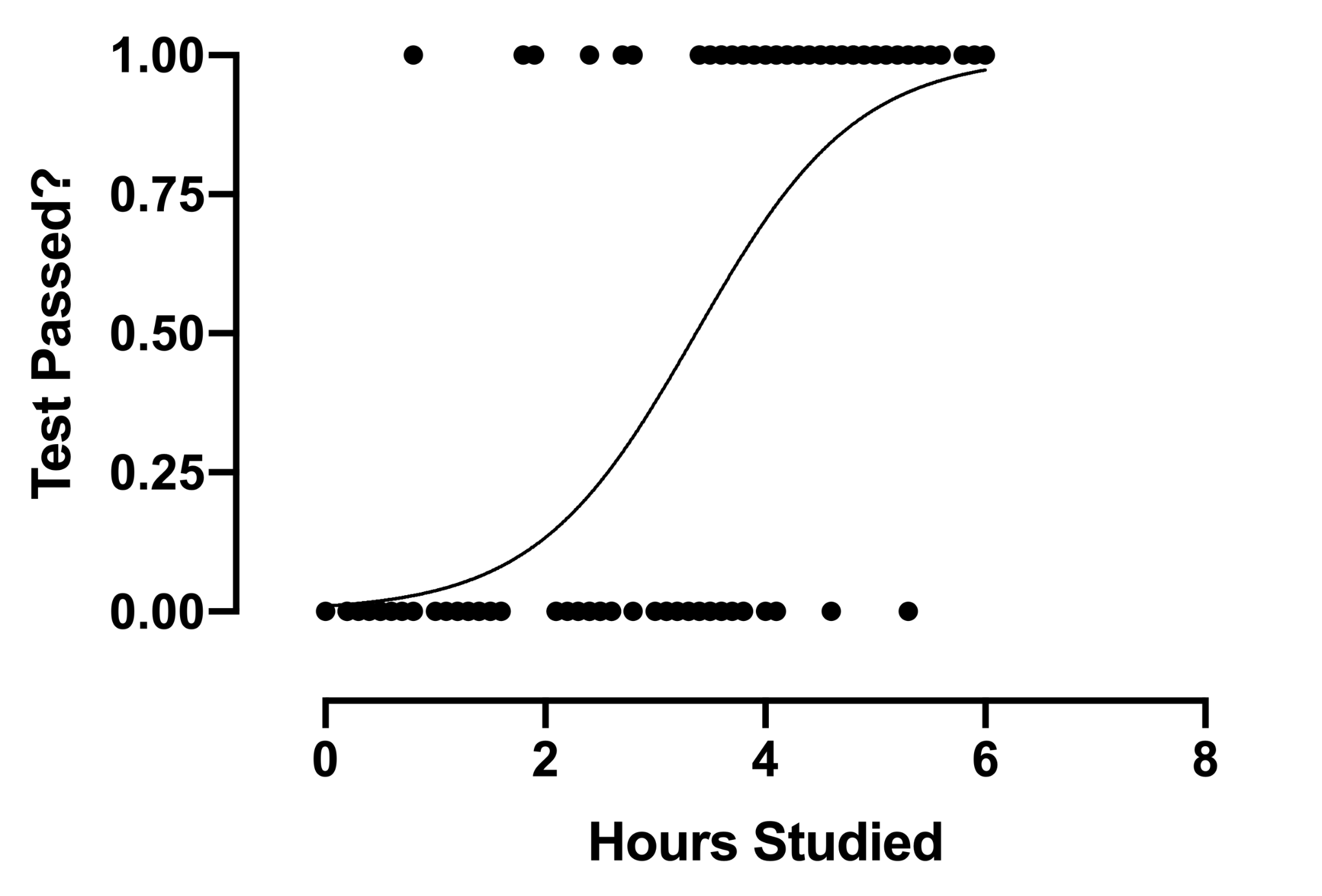
Fuente

3. Regresión polinomial

La técnica de análisis de regresión polinomial modela una relación no lineal entre las variables dependientes e independientes. Es una forma modificada del modelo de regresión lineal múltiple, pero la línea de mejor ajuste que pasa por todos los puntos de datos es curva y no recta.

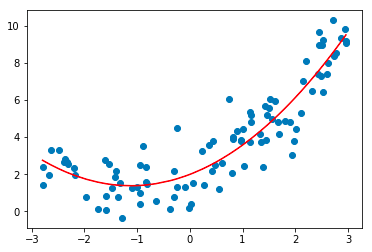
Fuente

4. Regresión de cresta

La técnica de análisis de regresión de cresta se utiliza cuando los datos muestran multicolinealidad; es decir, las variables independientes están altamente correlacionadas. Aunque las estimaciones de mínimos cuadrados en multicolinealidad no están sesgadas, sus variaciones son lo suficientemente grandes como para desviar el valor observado del valor real. La regresión de Ridge minimiza los errores estándar al introducir un grado de sesgo en las estimaciones de la regresión.

La lambda (λ) en la ecuación de regresión de la cresta resuelve el problema de la multicolinealidad.

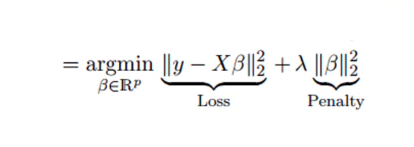
Fuente

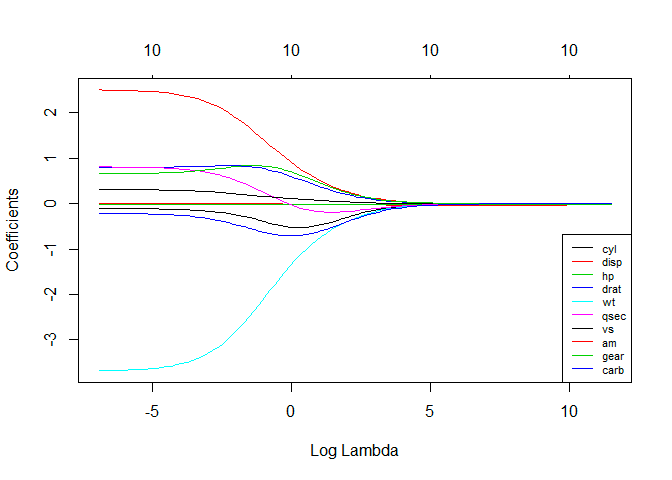
Fuente

5. Regresión de lazo

Al igual que la regresión de cresta, la técnica de regresión de lazo (operador de selección y contracción mínima absoluta) penaliza el tamaño absoluto del coeficiente de regresión. Además, la técnica de regresión de lazo utiliza la selección de variables, lo que da como resultado que los valores de los coeficientes se reduzcan hacia el cero absoluto.

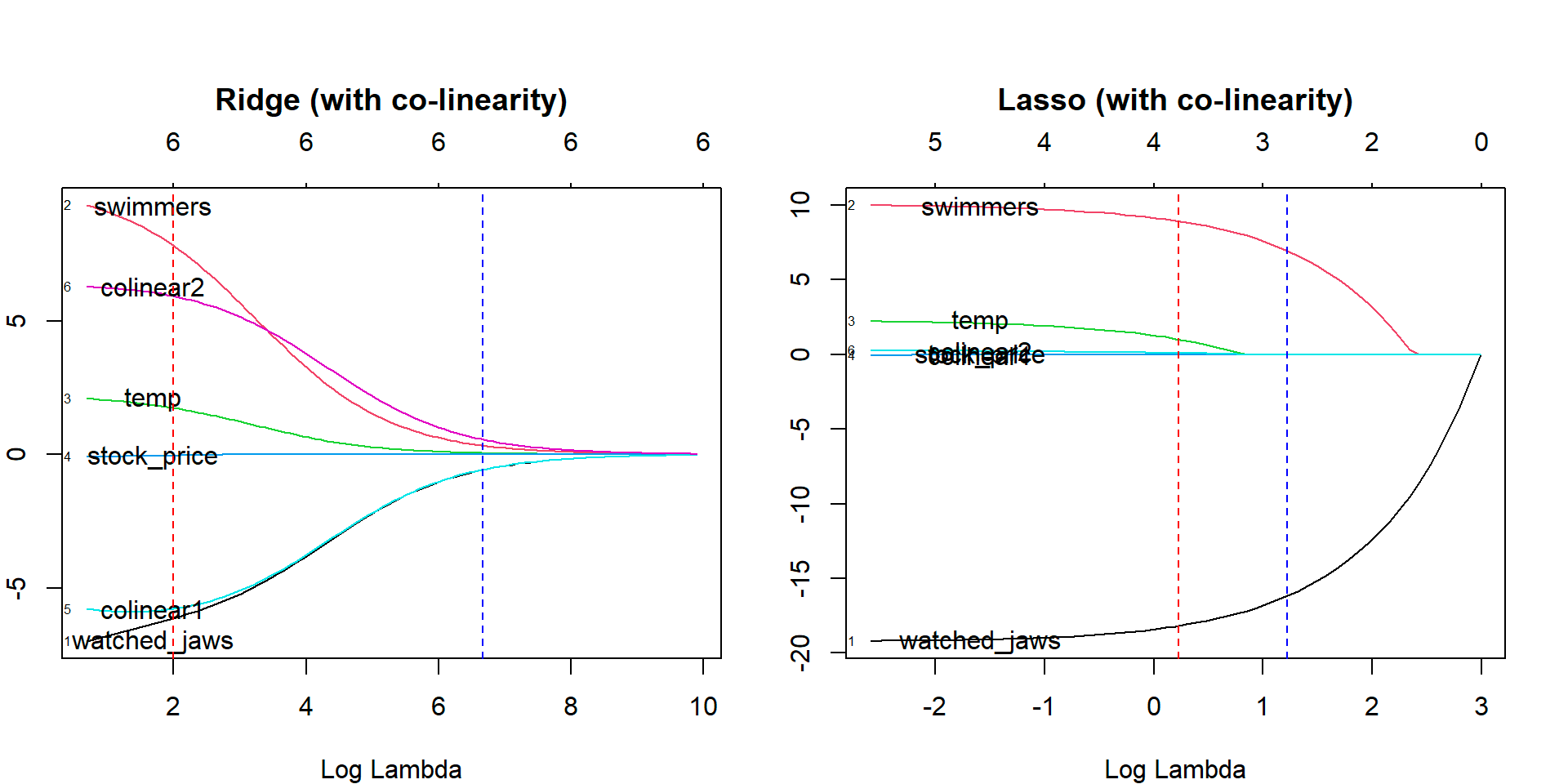
Fuente

6. Regresión por cuantiles

La técnica de análisis de regresión por cuantiles es una extensión del análisis de regresión lineal. Se utiliza cuando no se cumplen las condiciones para la regresión lineal o los datos tienen valores atípicos. La regresión cuantil encuentra aplicaciones en estadística y econometría.

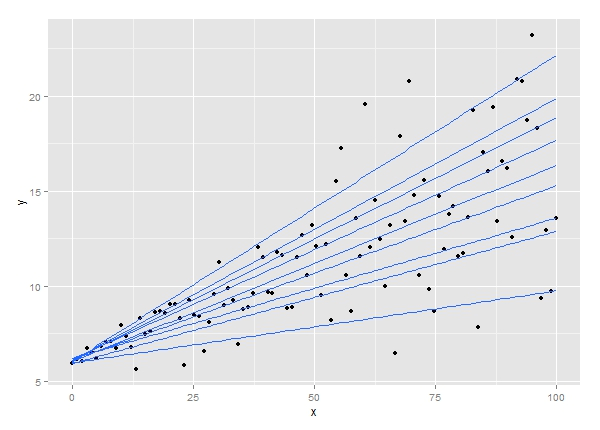
Fuente

7. Regresión lineal bayesiana

La regresión lineal bayesiana es uno de los tipos de técnicas de análisis de regresión en aprendizaje automático que utiliza el teorema de Bayes para determinar el valor de los coeficientes de regresión. En lugar de encontrar los mínimos cuadrados, esta técnica determina la distribución posterior de las características. Como resultado, la técnica tiene más estabilidad que la regresión lineal simple.

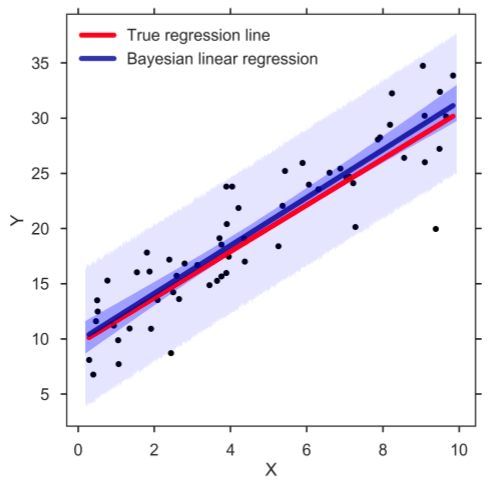
Fuente

8. Regresión de componentes principales

La técnica de regresión de componentes principales se utiliza normalmente para analizar datos de regresión múltiple con multicolinealidad. Al igual que la técnica de regresión de cresta, el método de regresión de componentes principales minimiza los errores estándar al impartir un grado de sesgo a las estimaciones de regresión. La técnica tiene dos pasos: primero, se aplica el análisis de componentes principales a los datos de entrenamiento y, luego, las muestras transformadas se usan para entrenar un regresor.

9. Regresión de mínimos cuadrados parciales

La técnica de regresión de mínimos cuadrados parciales es uno de los tipos rápidos y eficientes de técnicas de análisis de regresión basadas en la covarianza. Es beneficioso para los problemas de regresión donde el número de variables independientes es alto con probable multicolinealidad entre las variables. La técnica reduce las variables a un conjunto más pequeño de predictores, que luego se utilizan para realizar una regresión.

10. Regresión neta elástica

La técnica de regresión neta elástica es un híbrido de los modelos de regresión ridge y lazo y es útil cuando se trata de variables altamente correlacionadas. Utiliza las penalizaciones de los métodos de regresión ridge y lazo para regularizar los modelos de regresión.

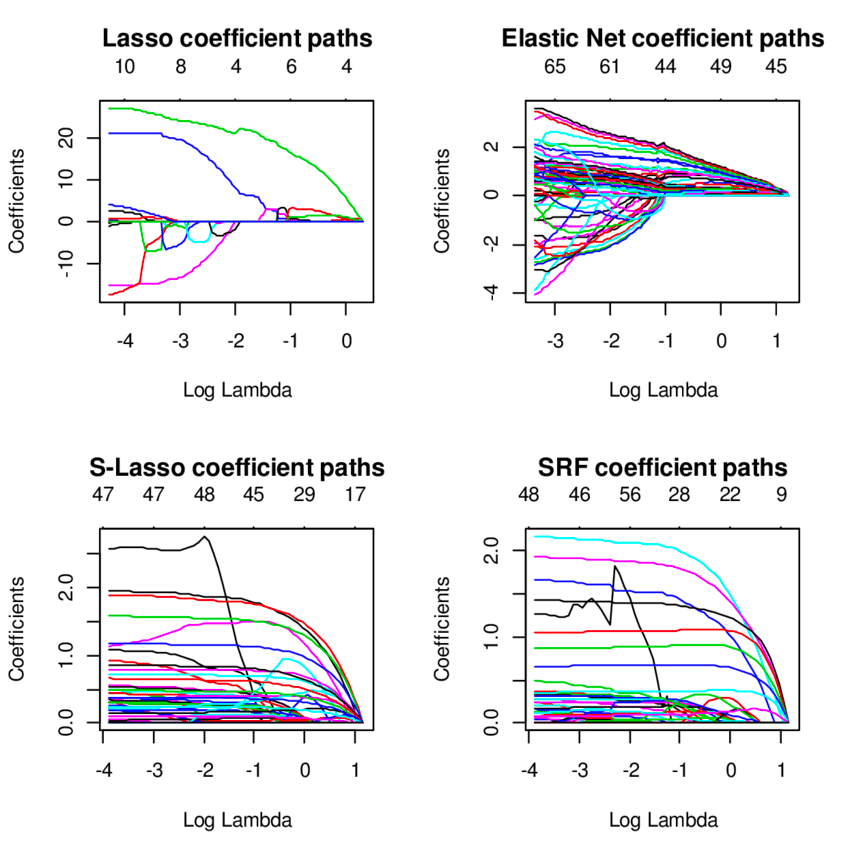
Fuente

Resumen

Además de las técnicas de análisis de regresión que analizamos aquí, se utilizan otros tipos de modelos de regresión en el aprendizaje automático, como la regresión ecológica, la regresión por pasos, la regresión de navaja y la regresión robusta. El caso de uso específico de todos estos diferentes tipos de técnicas de regresión depende de la naturaleza de los datos disponibles y el nivel de precisión que se puede lograr. En general, el análisis de regresión tiene dos ventajas principales. Estos son los siguientes:

• Indica la relación entre una variable dependiente y una variable independiente.

• Muestra la fuerza del impacto de las variables independientes sobre una variable dependiente.

El camino a seguir: Obtenga una Maestría en Ciencias en Aprendizaje Automático e IA

¿Está buscando un programa completo en línea para prepararse para una carrera de aprendizaje automático e inteligencia artificial?

upGrad ofrece una Maestría en Ciencias en Aprendizaje Automático e IA en asociación con la Universidad John Moores de Liverpool y el IIIT Bangalore para producir profesionales de IA y científicos de datos versátiles.

El completo programa en línea de 20 meses está diseñado específicamente para profesionales en activo que desean dominar conceptos y habilidades avanzados como Deep Learning, NLP, Graphical Models, Reinforcement Learning y similares. Además, el programa tiene la intención de impartir una base sólida en estadísticas junto con lenguajes de programación y herramientas clave como Python, Keras, TensorFlow, Kubernetes, MySQL y más.

Puntos destacados del programa:

• Maestría de la Universidad John Moores de Liverpool
• Ejecutivo PGP de IIIT Bangalore
• Más de 40 sesiones en vivo, más de 12 estudios de casos y proyectos, 11 asignaciones de codificación, seis proyectos finales
• Más de 25 sesiones de tutoría con expertos de la industria
• Asistencia profesional de 360 ​​grados y apoyo al aprendizaje
• Oportunidades de networking entre pares

Con una facultad de clase mundial, expertos en pedagogía, tecnología y la industria, upGrad se ha convertido en la plataforma EdTech superior más grande del sur de Asia y ha impactado a más de 500,000 profesionales en todo el mundo. Regístrate hoy ¡para formar parte de la base global de estudiantes de upGrad de más de 40 000 en más de 80 países!