Actualización de animación CSS con curvas de movimiento

Hay animación de interfaz de usuario y luego hay una buena animación de interfaz de usuario. Una buena animación te hace decir "¡Guau!" — es suave, hermoso y, sobre todo, natural, no en bloques, rígido o robótico. Si frecuentas Dribbble o UpLabs, sabrás de lo que hablo.

Lectura adicional sobre Smashing:

• Animaciones SVG y CSS con clip-path
• Técnicas prácticas de animación
• Creación de animaciones 'dibujadas a mano' con SVG
• La nueva API de animación web

Con tantos diseñadores increíbles creando animaciones tan hermosas, cualquier desarrollador naturalmente querría recrearlas en sus propios proyectos. Ahora, CSS proporciona algunos ajustes preestablecidos para transition-timing-function , como entrada ease-in , ease-out y ease-in-out , que agregan cierto nivel de suavidad y realismo, pero son muy genéricos, ¿no? ¿Qué tan aburrido sería si cada animación en la web siguiera las mismas tres funciones de tiempo?

Una de las propiedades de transition-timing-function es cubic-bezier(n1, n2, n3, n4) , en la que puede pasar cuatro números para crear su propia función de temporización. Hacia el final de este artículo, sabrá exactamente lo que representan estos cuatro números; aún así, créame, encontrar cuatro números para capturar la transición que está imaginando en su cabeza no es nada fácil. Pero gracias a cubic-bezier y Caesar, no tienes que hacerlo. Estas herramientas traen curvas de movimiento a la web.

Los animadores utilizan principalmente las curvas de movimiento (por ejemplo, en Adobe After Effects) para crear animaciones avanzadas y realistas. Con cubic-bezier y Ceasar, simplemente puede manipular la forma de una curva, y esos cuatro números ( n1, n2, n3, n4 ) se completarán por usted, ¡lo cual es absolutamente genial! Aún así, para usar y aprovechar al máximo las curvas de movimiento, debe comprender cómo funcionan, y eso es lo que haremos en este artículo. Vamos a empezar.

Comprender las curvas de movimiento

Una curva de movimiento no es más que un gráfico entre cualquier propiedad animable y el tiempo. Una curva de movimiento define cómo varía con el tiempo la velocidad de una animación que se ejecuta bajo su influencia.

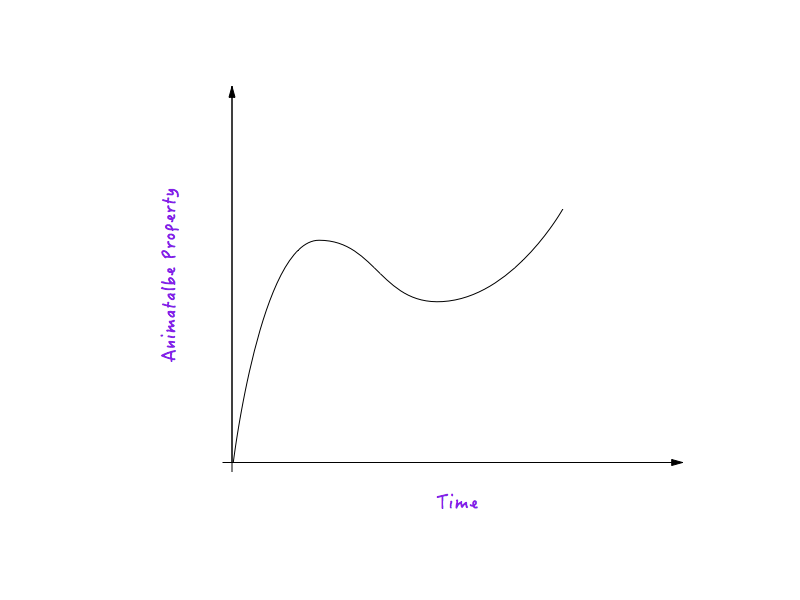
Tomemos la distancia ( translateX ) como un ejemplo de una propiedad animable. (La explicación es válida para cualquier otra propiedad animable).

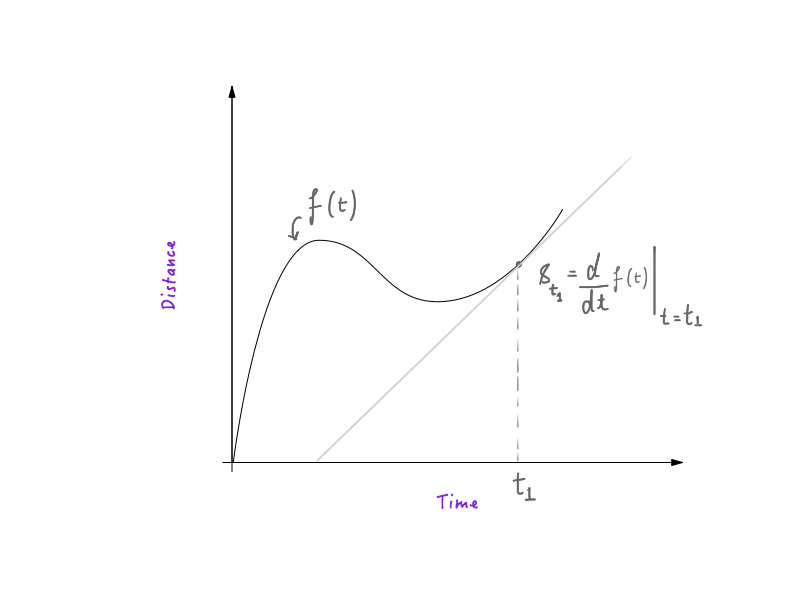
Si tienes alguna experiencia con la física y el cálculo básico, sabrás que descifrar la velocidad de un gráfico de distancia-tiempo es muy sencillo. La primera derivada de la distancia en función del tiempo , con respecto al tiempo , es la velocidad, lo que significa que un objeto que sigue una curva distancia-tiempo tendría mayor velocidad en los lugares donde la curva es pronunciada y menor en los lugares donde la curva es más plana. . Si sabes cómo funciona, ¡genial! Ya está todo listo y puede pasar a la siguiente sección.

Ahora, soy consciente de que el diseño y el desarrollo es un campo diverso, y no todos tienen los mismos antecedentes. Tal vez los dos párrafos anteriores fueron toda una jerga para usted. No te preocupes. Continuaremos y le daremos sentido a la jerga.

Considere el cuadro rojo a continuación. Pongámonos un poco inexpertos aquí y llamemos al cuadro rojo "Boxy"; será más fácil referirse a él de esa manera. Muy bien, Boxy se moverá de un borde de la pantalla al otro de forma lineal, y vamos a analizar su movimiento.

Uno de los ajustes preestablecidos de transition-timing-function es linear . Para hacer que Boxy se mueva, todo lo que hacemos es agregar la siguiente clase.

 .moveForward { transform: translateX(1000px); }

Para controlar la animación, estableceríamos la propiedad de transition para Boxy de la siguiente manera:

 #boxy { width: 200px; height: 200px; background: red; transition-property: transform; transition-duration: 1s; transition-timing-function: linear; }

Esa es una forma muy detallada de especificar la transition . En realidad, casi siempre encontrará transition escrita en su forma abreviada:

 #boxy { width: 200px; height: 200px; background: red; transition: transform 1s linear; }

Vamos a verlo ir.

Robótica, ¿no? Se podría decir que este movimiento se siente robótico porque es lineal, lo cual es una respuesta perfectamente plausible. Pero, ¿podrías explicar por qué? Podemos ver que la configuración linear da como resultado un movimiento robótico, pero ¿qué sucede exactamente detrás de escena? Eso es lo que descubriremos primero; vamos a llegar a las entrañas y entender por qué este movimiento se siente robótico, en bloque y no natural.

Comencemos graficando el movimiento de Boxy para ver si podemos obtener una idea. Nuestro gráfico tendrá dos ejes, siendo el primero la distancia y el segundo el tiempo. Boxy cubre una distancia total de 1000 píxeles (distancia) en 1 segundo (tiempo). Ahora, no se asuste por todas las matemáticas a continuación, es muy simple.

Aquí está nuestro gráfico muy simple, con los ejes como se mencionó.

Ahora mismo, está vacío. Rellenémoslo con algunos datos.

Para empezar, sabemos que a los 0 segundos, cuando aún no ha comenzado la animación, Boxy está en su posición inicial (0 píxeles). Y después de que haya pasado 1 segundo, Boxy ha viajado un total de 1000 píxeles, aterrizando en el borde opuesto de la pantalla.

Tracemos estos datos en el gráfico.

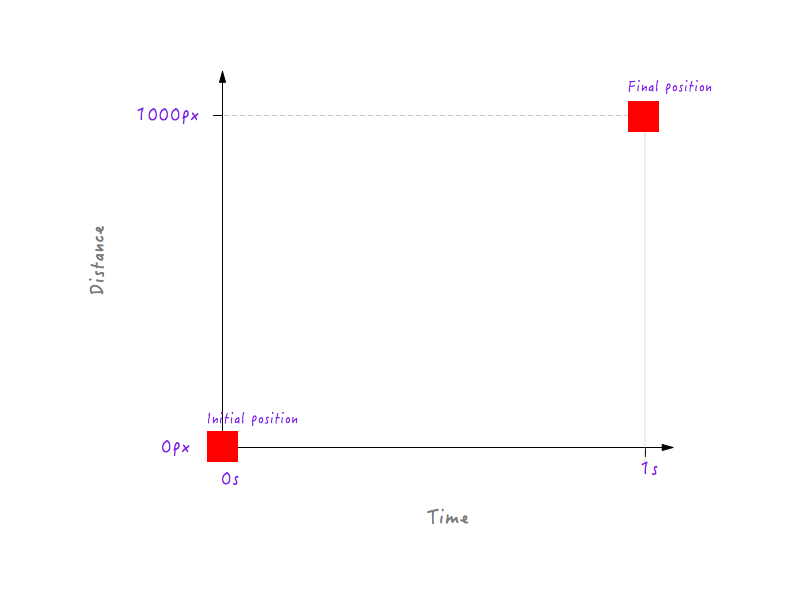
Hasta aquí todo bien. Pero dos puntos de datos no son suficientes, necesitamos más. La siguiente figura muestra las posiciones de Boxy en diferentes momentos (todo gracias a mi cámara de alta velocidad).

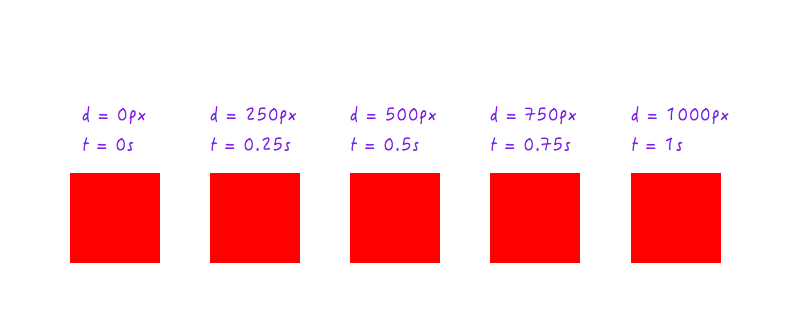
Agreguemos estos datos a nuestro gráfico.

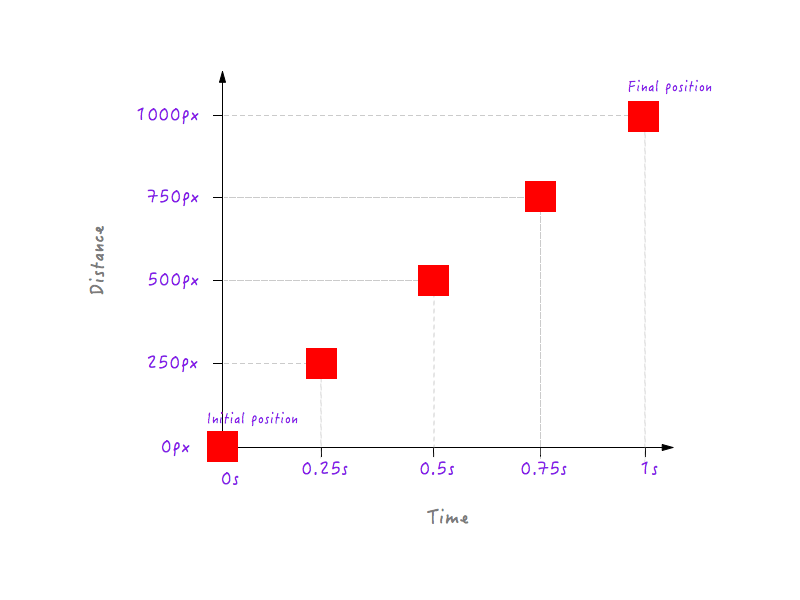
Por supuesto, podría tener muchos más puntos de datos para diferentes tiempos (por ejemplo, 0,375 segundos, 0,6 segundos, etc.), pero lo que tenemos es suficiente para completar nuestro gráfico. Al unir todos los puntos, hemos completado el gráfico. ¡Cinco altos!

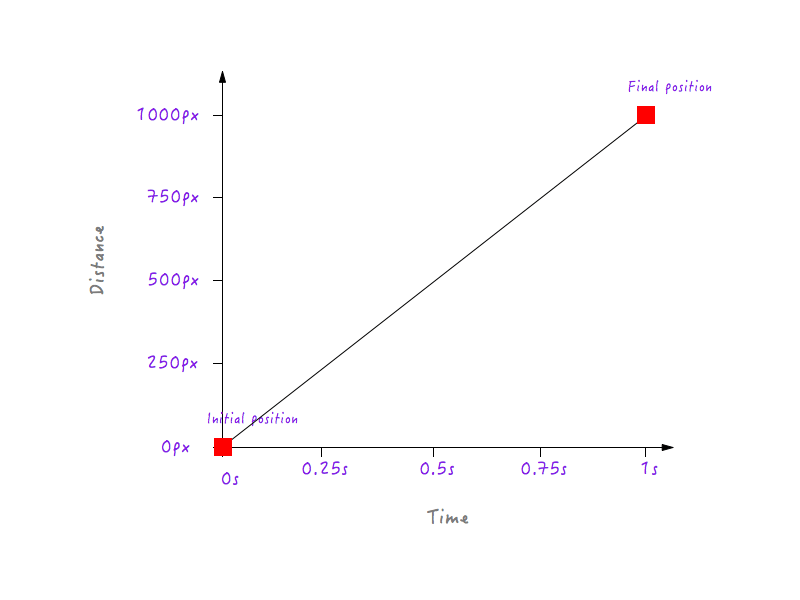
Genial, pero ¿qué nos dice esto? ¿Recuerdas que comenzamos nuestra investigación con el objetivo de comprender por qué el movimiento lineal de Boxy se siente antinatural y robótico? De un vistazo, este gráfico que acabamos de construir no nos dice nada al respecto. Necesitamos ir más profundo.

Tenga en cuenta el gráfico y hablemos un minuto sobre la velocidad. Sé que sabes lo que es la velocidad; me gustaría expresarlo en términos matemáticos. Como va, la fórmula para la velocidad es esta:

Por tanto, si un coche recorre una distancia de 100 kilómetros en 1 hora, decimos que su velocidad es de 100 kilómetros por hora.

Si el coche duplica su velocidad, empezará a recorrer el doble de distancia (200 kilómetros) en el mismo intervalo (1 hora), es decir, recorrerá la distancia original de 100 kilómetros en la mitad de tiempo (0,5 horas). . ¿Tener sentido?

De manera similar, si el automóvil redujera a la mitad su velocidad (es decir, ralentizara a la mitad), comenzaría a recorrer una distancia de 50 kilómetros en el mismo intervalo (1 hora), o, en otras palabras, recorrería la distancia original de 100 kilómetros. kilómetros en el doble de tiempo (2 horas).

¡Genial! Con eso fuera del camino, retomemos donde lo dejamos. Tratábamos de averiguar cómo la gráfica entre la distancia y el tiempo puede ayudarnos a comprender por qué el movimiento lineal de Boxy parece robótico.

¡Oye, espera un segundo! Tenemos un gráfico entre la distancia y el tiempo, y la velocidad se puede calcular a partir de la distancia y el tiempo, ¿no? Tratemos de calcular la velocidad de Boxy en diferentes intervalos de tiempo.

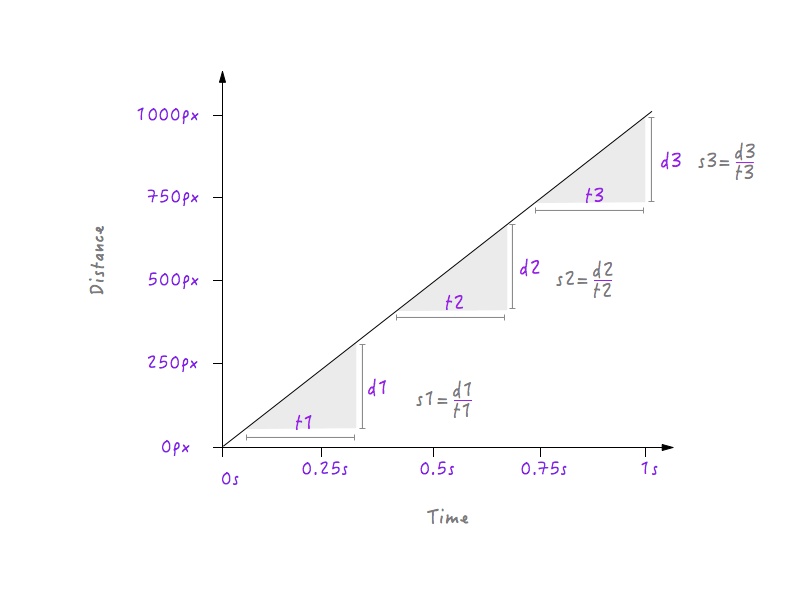
Aquí, he elegido tres intervalos de tiempo diferentes: uno cerca del inicio, uno en el medio y uno al final cerca de la posición final. Como es evidente, en los tres intervalos, Boxy tiene exactamente la misma velocidad (s1 = s2 = s3) de 1000 píxeles por segundo; es decir, independientemente del intervalo que elija en el gráfico anterior, encontrará a Boxy moviéndose a 1000 píxeles por segundo. ¿No es extraño? Las cosas en la vida real no se mueven a una velocidad constante; comienzan lentamente, aumentan gradualmente su velocidad, se mueven por un tiempo y luego reducen la velocidad nuevamente antes de detenerse, pero Boxy comienza abruptamente con una velocidad de 1000 píxeles por segundo, se mueve con la misma velocidad y se detiene abruptamente exactamente a la misma velocidad. Es por eso que el movimiento de Boxy se siente robótico y poco natural. Vamos a tener que cambiar nuestro gráfico para arreglar esto. Pero antes de sumergirnos, necesitaremos saber cómo los cambios en la velocidad afectarán el gráfico dibujado entre la distancia y el tiempo. ¿Listo? Esto va a ser divertido.

Dupliquemos la velocidad de Boxy y veamos cómo cambia la apariencia del gráfico en respuesta. La velocidad original de Boxy, como calculamos anteriormente, es de 1000 píxeles por segundo. Como hemos duplicado la velocidad, Boxy ahora podrá cubrir la distancia de 1000 píxeles en la mitad del tiempo, es decir, en 0,5 segundos. Pongámoslo en un gráfico.

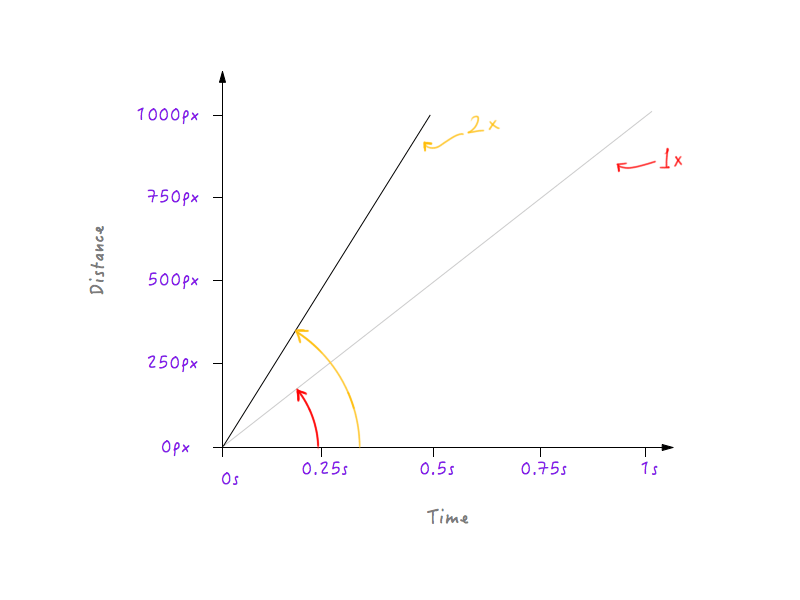
¿Y si triplicamos la velocidad? Boxy ahora cubre 1000 píxeles en un tercio del tiempo (un tercio de segundo).

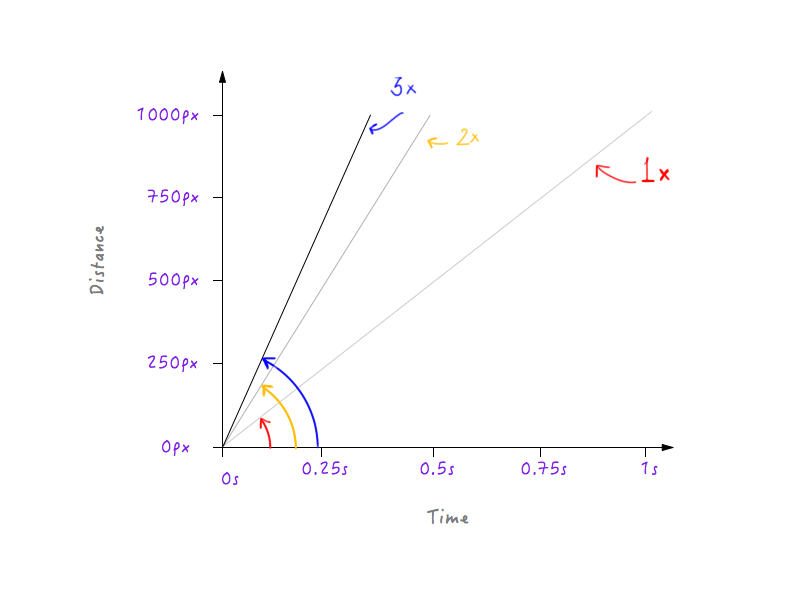
Hmm, ¿notas algo? Observa cómo, cuando cambia la gráfica, el ángulo que forma la línea con el eje del tiempo aumenta a medida que aumenta la velocidad.

Muy bien, sigamos adelante y reduzcamos a la mitad la velocidad de Boxy. Reducir a la mitad su velocidad significa que Boxy podrá cubrir solo 500 píxeles (la mitad de la distancia original) en 1 segundo. Pongamos esto en un gráfico.

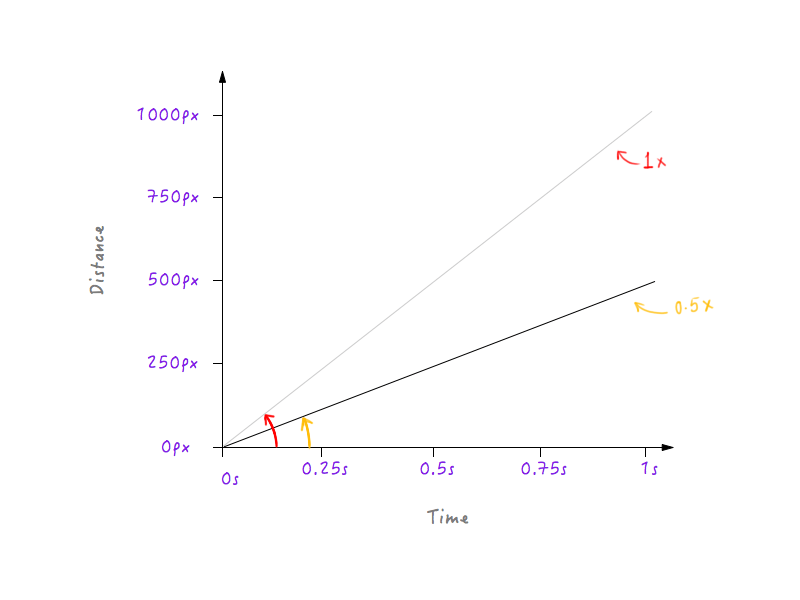
Reduzcamos la velocidad de Boxy un poco más, haciendo que la velocidad sea un tercio de la original. Boxy podrá cubrir un tercio de la distancia original en 1 segundo.

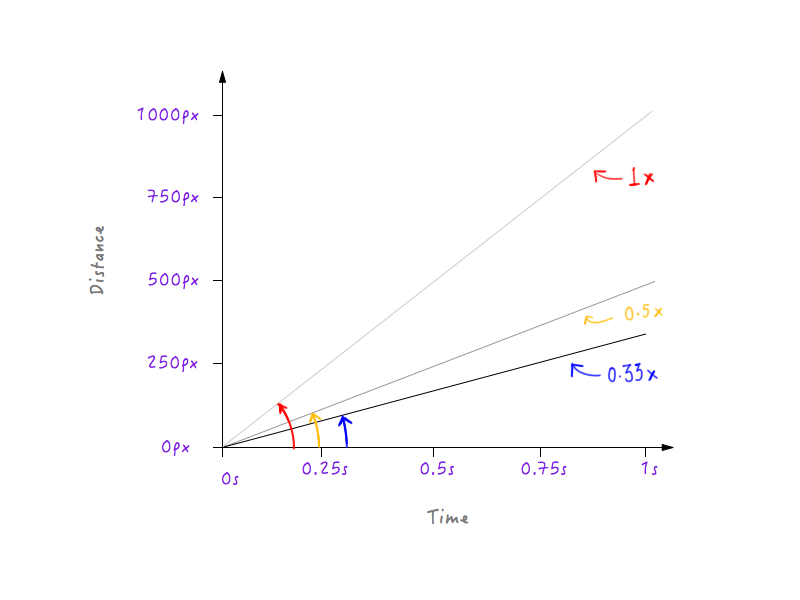
¿Ves un patrón? La línea se vuelve más y más empinada a medida que aumentamos la velocidad de Boxy, y comienza a aplanarse a medida que disminuimos la velocidad de Boxy.

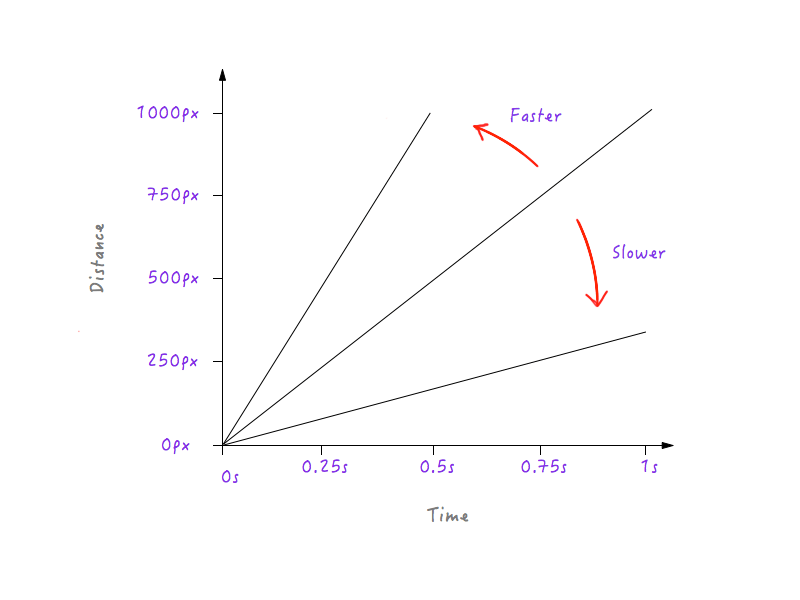
Esto tiene sentido porque, para una línea más empinada, un pequeño avance en el tiempo produce un cambio mucho mayor en la distancia, lo que implica una mayor velocidad.

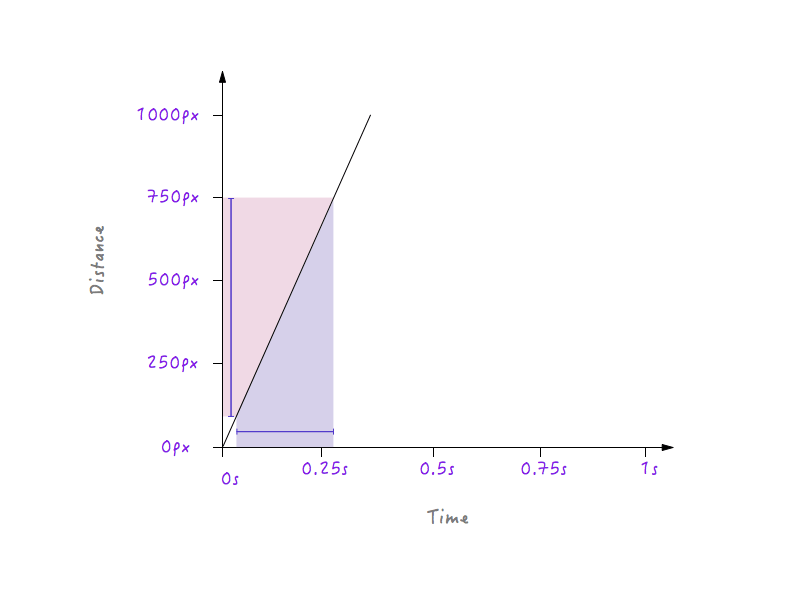
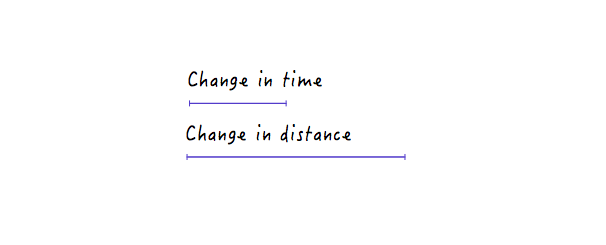
Por otro lado, para una línea menos empinada, un gran cambio en el tiempo produce solo un pequeño cambio en la distancia, lo que significa una velocidad más baja.

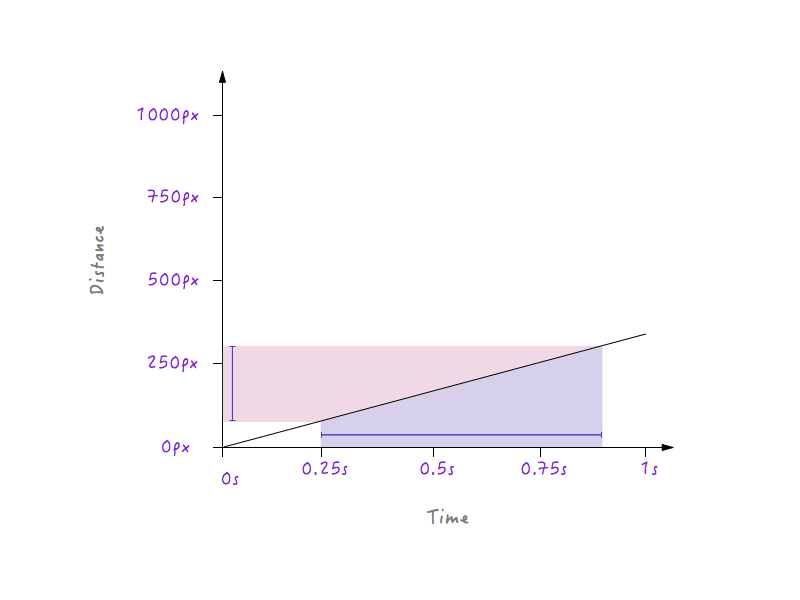
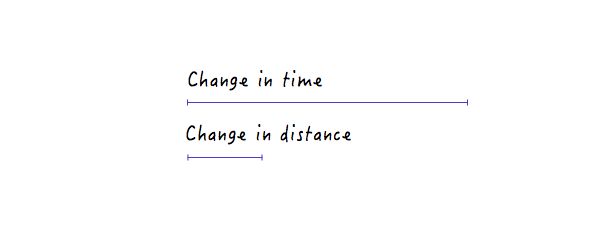
Con todos los cambios que hemos realizado, Boxy sigue moviéndose de forma lineal, solo que a diferentes velocidades. Sin embargo, con nuestro conocimiento recién adquirido de cómo los cambios en la distancia versus el tiempo pueden afectar la velocidad, podemos experimentar y dibujar un gráfico que haga que Boxy se mueva de una manera que parezca natural y realista.

Vamos a hacerlo paso a paso. Primero, las cosas en la vida real comienzan lentamente y aumentan lentamente de velocidad. Entonces, hagamos eso.

En todas las iteraciones del gráfico que se muestra a continuación, notará que los puntos en las esquinas opuestas permanecen fijos. Esto se debe a que no cambiamos la duración de la ejecución de la animación ni la distancia que recorre Boxy.

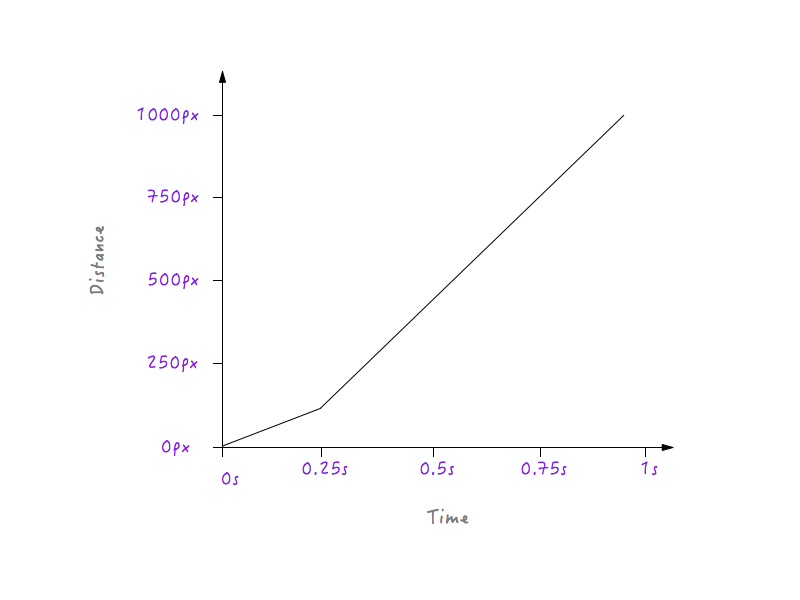
Si Boxy va a seguir el gráfico anterior, se moverá a una velocidad más lenta durante 0,25 segundos, porque la línea es menos empinada a partir de 0 a 0,25 segundos, y luego cambiará abruptamente a una velocidad más alta después de 0,25 segundos (la razón es que la línea en el gráfico se vuelve más pronunciada después de 0,25 segundos). Sin embargo, tendremos que suavizar esta transición; no queremos esquinas; después de todo, se llama curva de movimiento. Convirtamos esa esquina en una curva.

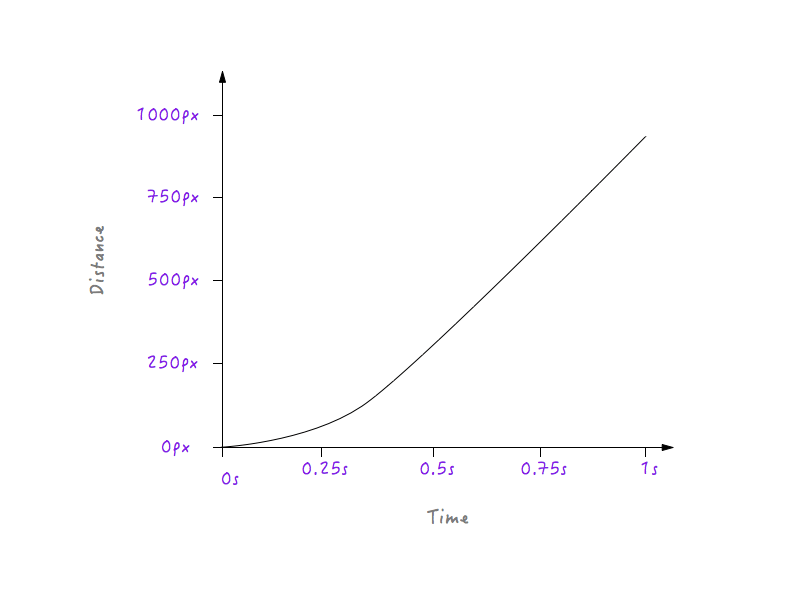
Observe la suave transición que sufre Boxy desde el reposo hasta el aumento gradual de la velocidad.

¡Bien! A continuación, los objetos de la vida real se ralentizan progresivamente antes de detenerse. Cambiemos la gráfica para que eso suceda. Nuevamente, seleccionaremos un punto en el tiempo después del cual nos gustaría que Boxy comience a disminuir la velocidad. ¿Qué tal alrededor de 0,6 segundos? Ya he suavizado la esquina de la transición a una curva aquí.

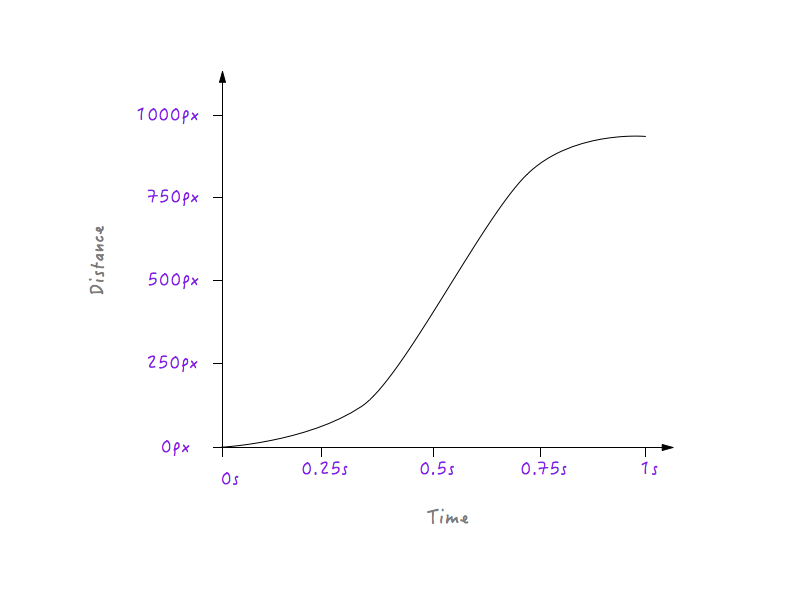
Mira Boxy ir! Mucho más natural, ¿no?

La curva que dibujamos en lugar de la esquina es en realidad una colección de muchos segmentos de línea pequeños; y, como ya sabes, cuanto más inclinada es la línea en el gráfico, mayor es la velocidad, y cuanto más plana es la línea, más lenta es la velocidad. Observe cómo en la parte izquierda de la imagen, los segmentos de línea que forman la curva se vuelven cada vez más pronunciados, lo que resulta en un aumento gradual de la velocidad, y se aplanan progresivamente en el lado derecho, lo que hace que la velocidad disminuya progresivamente.

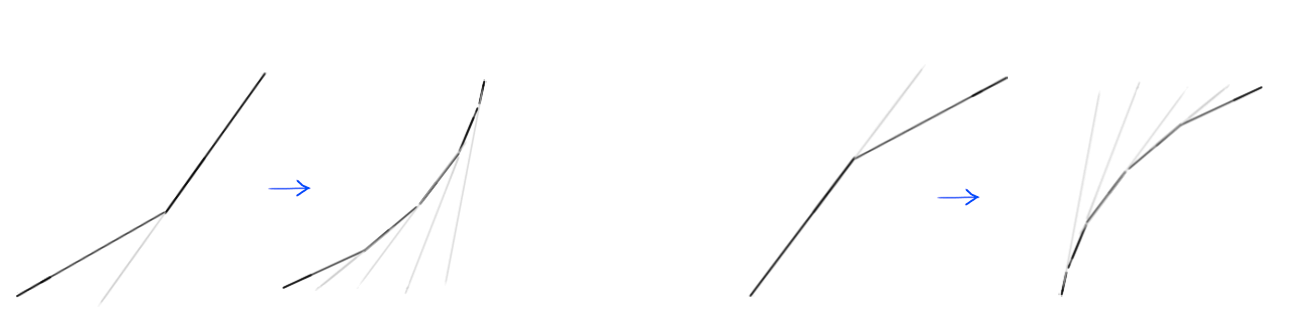
Con todo este conocimiento, dar sentido a las curvas de movimiento se vuelve mucho más fácil. Veamos algunos ejemplos.

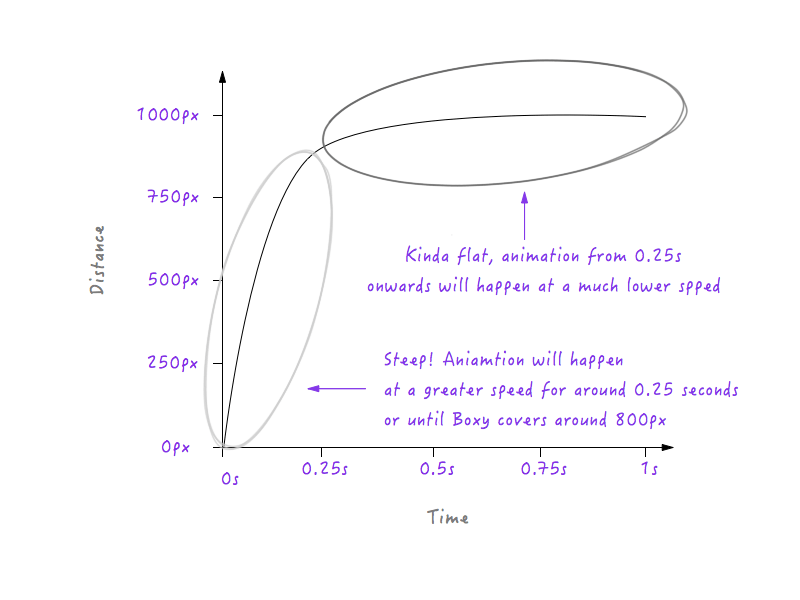
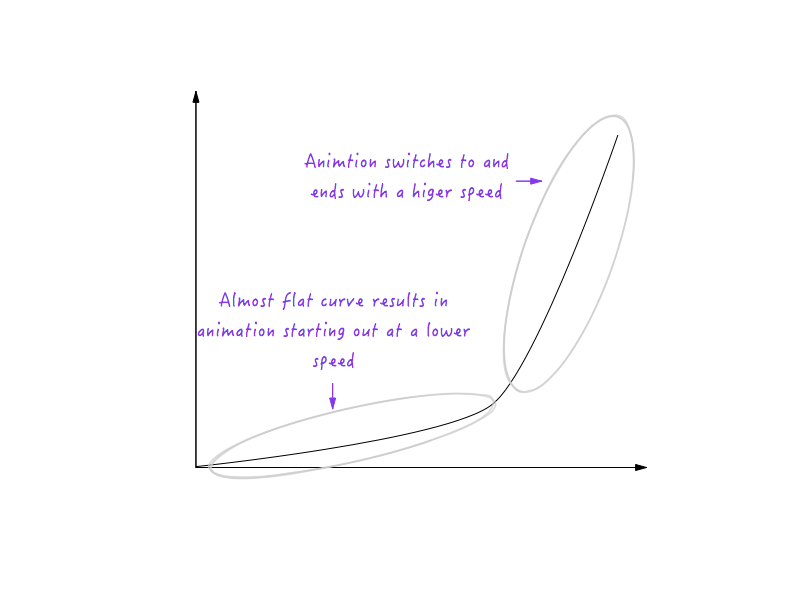
Uso de curvas de movimiento en animación de interfaz de usuario

La próxima vez que tenga que animar un elemento de la interfaz de usuario, tendrá a su disposición el poder de las curvas de movimiento. Ya sea que se trate de una barra deslizable, una ventana modal o un menú desplegable, agregar la cantidad correcta de animación y hacer que se vea suave y natural aumentará en gran medida la calidad de la interfaz de usuario. Hará que la interfaz de usuario se sienta bien. Tome el menú deslizable a continuación:

Al hacer clic en el menú de hamburguesas, aparece el menú de la izquierda, pero la animación se siente bloqueada. La línea 51 del CSS muestra que la animación tiene transition-timing-function establecida en linear . Podemos mejorar esto. Vayamos a cubic-bezier y creemos una función de temporización personalizada.

Si está leyendo esto, es seguro asumir que es un diseñador o un desarrollador o ambos y, por lo tanto, no es ajeno a las curvas cúbicas de Bézier; hay una buena posibilidad de que los hayas encontrado al menos una vez. Las curvas de Bezier son una maravilla. Se utilizan principalmente en gráficos por computadora para dibujar formas y en herramientas como Sketch y Adobe Illustrator para dibujar gráficos vectoriales. La razón por la que las curvas cúbicas de Bézier son tan populares es que son muy fáciles de usar: simplemente modifique las posiciones de los cuatro puntos diferentes y cree el tipo de curva que necesita.

Como siempre conocemos los estados inicial y final del objeto animado, podemos arreglar dos de los puntos. Eso deja solo dos puntos cuyas posiciones tenemos que modificar. Los dos puntos fijos se denominan puntos de anclaje y los dos restantes son puntos de control.

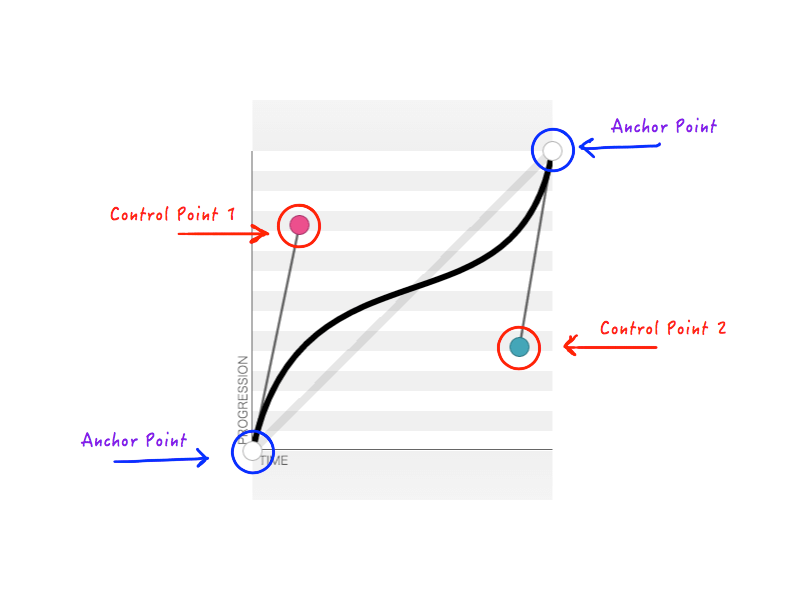
Como recordará, cubic-bezier acepta cuatro números ( n1, n2, n3, n4 ) cuando crea una transition-timing-function personalizada. Estos cuatro números representan nada más que las posiciones de los dos puntos de control: n1, n2 representan las coordenadas x e y del primer punto de control, y n3, n4 representan las coordenadas del segundo punto de control. Debido a que cambiar la posición de los puntos de control cambiará la forma de la curva y, por lo tanto, nuestra animación en general, el resultado es el mismo cuando se modifica cualquiera o todos los n1, n2, n3, n4 . Por ejemplo, la siguiente figura representa cubic-bezier(.14, .78, .89, .35) :

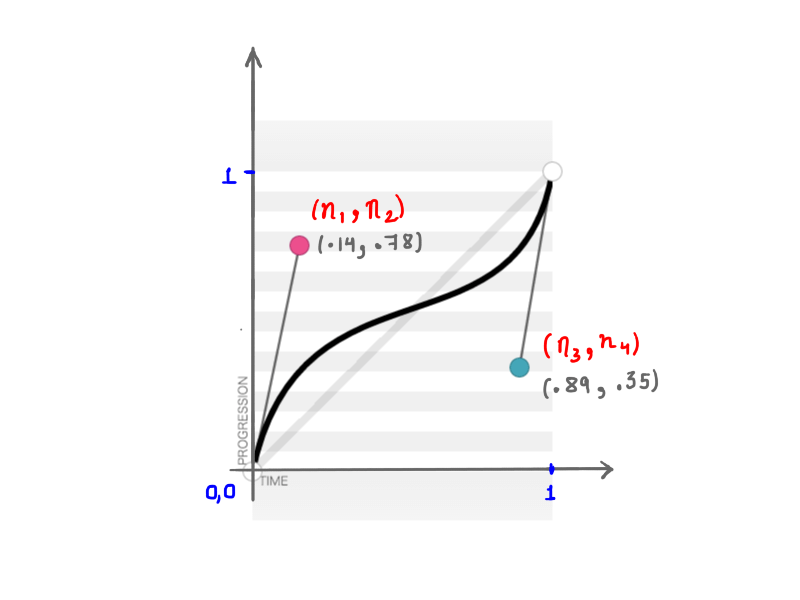
Las matemáticas detrás de estas curvas aparentemente simples son fascinantes.

Muy bien, muy bien, volvamos a donde estábamos yendo con cubic-bezier: crear una transition-timing-function personalizada. Quiero el tipo de animación en la que el menú se desliza muy rápido y luego se ralentiza con gracia y termina:

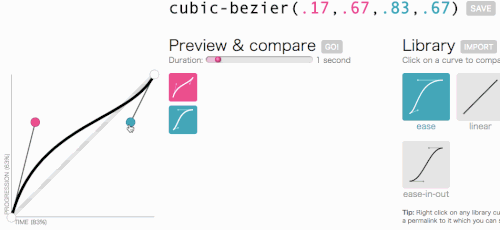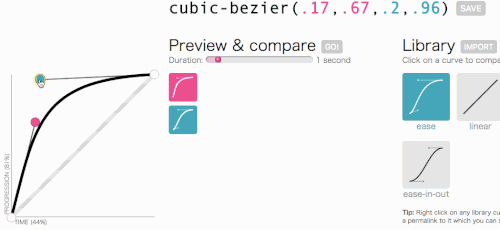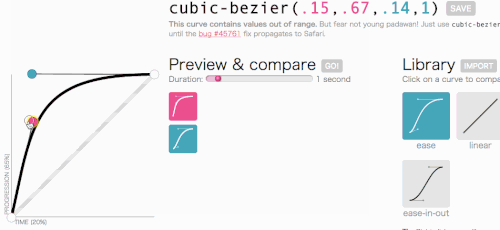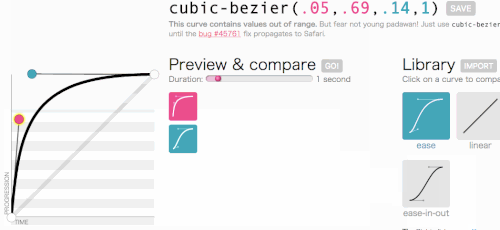
Esto luce bien. La animación comenzará rápido y luego se ralentizará, en lugar de moverse a una velocidad constante en todo momento. Simplemente voy a copiar cubic-bezier(.05, .69, .14, 1) desde la parte superior de la página y reemplazaré linear con él.

¿Ver la diferencia? La segunda iteración se siente mucho más natural y atractiva. Imagínese si cada animación en su interfaz de usuario siguiera una función de tiempo natural. ¿Qué tan genial sería eso?

Como hemos visto, las curvas de movimiento no son complicadas en absoluto. Son muy fáciles de entender y usar. Con ellos, puede llevar su interfaz de usuario al siguiente nivel.

Espero que hayas aprendido cómo funcionan las curvas de movimiento. Si estaba pasando por muchas pruebas y errores para que las curvas de movimiento funcionaran de la manera que desea, o si no las estaba usando en absoluto, ahora debería sentirse cómodo doblándolas a su voluntad y creando hermosas animaciones. Porque, después de todo, la animación importa.