Derivada de la regla de la cadena en el aprendizaje automático: explicación

El aprendizaje automático ha evolucionado hasta convertirse en uno de los campos más discutidos e investigados en los últimos años, y por todas las buenas razones. Todos los días se descubren nuevos modelos y aplicaciones de aprendizaje automático, e investigadores de todo el mundo están trabajando para lograr el próximo gran avance.

Como resultado, ha habido un mayor interés en los profesionales de diversos orígenes para cambiar al aprendizaje automático y ser parte de esta revolución en curso. Si usted es uno de esos entusiastas del aprendizaje automático que busca dar sus primeros pasos, le diremos que comienza con la comprensión de los conceptos básicos de matemáticas y estadísticas antes que nada.

Uno de esos temas vitales en Matemáticas que es muy relevante para el aprendizaje automático son los derivados. De su comprensión básica del cálculo, recordaría que la derivada de cualquier función es la tasa de cambio instantánea de esa función. En este blog, profundizaremos en las derivadas y exploraremos la regla de la cadena. Veremos cómo cambia la salida de una función particular cuando cambiamos algunas variables independientes en la ecuación. Con el conocimiento de las derivadas de la regla de la cadena, podrá trabajar en la diferenciación de funciones más complejas que seguramente encontrará en el aprendizaje automático.

Obtenga la certificación de Machine Learning en línea de las mejores universidades del mundo: maestrías, programas ejecutivos de posgrado y programa de certificado avanzado en ML e IA para acelerar su carrera.

Comprender la derivada de la regla de la cadena

La regla de la cadena es esencialmente una fórmula matemática que te ayuda a calcular la derivada de una función compuesta. Una función compuesta es aquella que se compone de dos o más funciones. Entonces, si f y g son dos funciones, entonces la regla de la cadena nos ayudaría a encontrar la derivada de funciones compuestas como fog o go f.

Teniendo en cuenta la niebla de la función compuesta, así es como se vería la derivada de la regla de la cadena:

La regla anterior también se puede escribir como:

Donde la función F es la composición de f y g , en la forma de f(g(x)).

Ahora, supongamos que tenemos tres variables tales que la tercera variable (z) depende de la segunda variable (y), que a su vez depende de la primera variable (x). En ese caso, la derivada de la regla de la cadena se vería así:

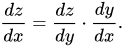En términos de aprendizaje profundo, esta también es la fórmula que se usa regularmente para resolver problemas de retropropagación. Ahora, como mencionamos que z depende de y y y de x, podemos escribir z = f(y) y y = g(x). Esta sustitución modificaría nuestra ecuación diferencial de la siguiente manera:

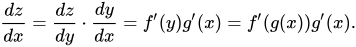Ahora, veamos algunos ejemplos de derivados de la regla de la cadena para comprender mejor las matemáticas detrás de ellos.

Ejemplos y aplicaciones de la derivada de la regla de la cadena

Tomemos un ejemplo bien conocido de Wikipedia para comprender mejor la derivada de la regla de la cadena. Suponga que está tomando una caída libre desde el cielo. La presión atmosférica que encuentres durante el otoño seguirá cambiando constantemente. Aquí hay un gráfico que traza este cambio de presión atmosférica con niveles de elevación:

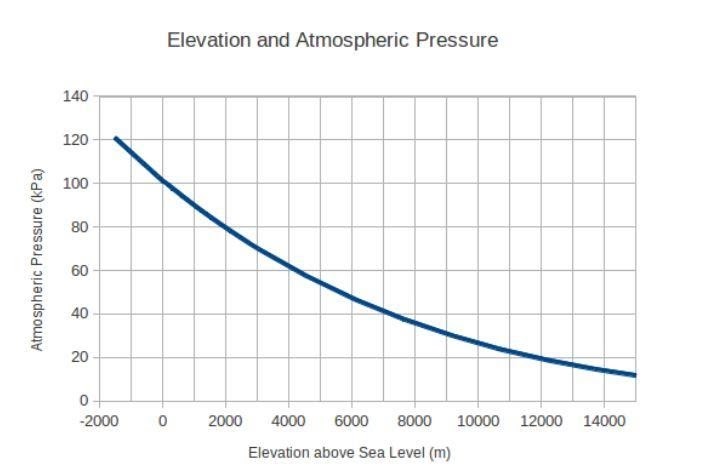
Suponga que su caída comenzó a 4000 metros sobre el nivel del mar. Inicialmente, su velocidad era cero y el valor de la aceleración era de 9,8 metros por segundo al cuadrado debido a la gravedad.

Ahora, comparemos esta situación con el método anterior de la regla de la cadena. En este ejemplo, usaremos la variable 't' para el tiempo en lugar de x.

Entonces, la variable y = g(t), que indica la distancia recorrida desde el comienzo de la caída, se puede dar como:

g(t) = 0.5*9.8t^2

Y, la altura desde el nivel del mar puede estar dada por una variable 'h', que será igual a 400-g(t).

Suponga que, con base en un modelo, también podemos escribir la función de la presión atmosférica a cualquier altura h como:

f(h) = 101325 e−0.0001h

Ahora, puede distinguir entre las dos ecuaciones en función de sus variables dependientes para obtener los siguientes resultados:

g′(t) = −9.8t,

Aquí, g'(t) indica el valor de su velocidad en cualquier momento t.

f′(h) = −10.1325e−0.0001h

Aquí, f′(h) es la tasa de cambio de la presión atmosférica con respecto a la altura h. Ahora, la pregunta es ¿podemos combinar estas dos ecuaciones y derivar la tasa de cambio de la presión atmosférica en función del tiempo? Veamos usando la regla de la cadena:

La ecuación final que tenemos nos proporciona la tasa de cambio de la presión atmosférica en relación con el tiempo transcurrido desde la caída. En términos de aprendizaje automático, las redes neuronales necesitan constantemente actualizaciones de peso con respecto al error de predicción de la neurona. La regla de la cadena ayuda a ajustar estos pesos y acerca el modelo de aprendizaje automático a la salida correcta.

Conclusión

Como puede ver, la regla de la cadena es beneficiosa para muchos propósitos. Especialmente cuando se trata de aprendizaje automático o aprendizaje profundo, la regla de la cadena resulta muy útil para actualizar los pesos de las neuronas y mejorar la eficiencia general del modelo.

Ahora que conoce los conceptos básicos de la regla de la cadena, siga adelante e intente algunos problemas por su cuenta. Busque algunas funciones compuestas e intente encontrar sus derivadas. ¡Cuanto más practique, más claros se volverán sus conceptos y más fácil le resultará entrenar sus modelos de aprendizaje automático! Dicho esto, si eres un entusiasta del aprendizaje automático pero tienes dificultades para dar tus primeros pasos en este campo, ¡upGrad te respalda!

Nuestro programa Executive PG en aprendizaje automático e inteligencia artificial se ofrece en colaboración con IIIT-Bangalore y le brinda la opción de elegir entre seis especializaciones relevantes para la industria. El curso comienza desde el nivel básico y lo lleva a la cúspide mientras le brinda apoyo 1 a 1 de expertos de la industria, un sólido grupo de estudiantes y apoyo profesional de 360 ​​grados.