Árbol binario vs árbol de búsqueda binaria: diferencia entre árbol binario y árbol de búsqueda binaria
Publicado: 2021-01-21Tabla de contenido
Introducción
La clasificación es el proceso de organizar los datos en un orden sistemático para que puedan analizarse de manera más efectiva. El proceso de identificar un registro en particular se llama búsqueda. Si los datos se clasifican correctamente en un orden particular, la búsqueda se convierte en una tarea fácil y eficiente. Este artículo trata sobre una de las estructuras de datos no lineales más importantes, es decir, los árboles.
Los árboles se utilizan principalmente para representar datos demostrando una relación jerárquica entre los elementos. Por ejemplo, índice, árbol genealógico. Técnicamente, un árbol puede definirse como un conjunto finito 'T' de uno o más nodos, de modo que un nodo se asigna como raíz del árbol y los otros nodos se dividen en n>=0 conjuntos disjuntos T1, T2, T3, T4…. Tn y se denominan subárboles o hijos de ese nodo raíz.
¿Qué es un árbol binario?
Un árbol binario es una estructura de datos no lineal en la que un nodo puede tener 0, 1 o 2 nodos. Cada nodo en el árbol binario se denomina nodo principal o nodo secundario. El nodo superior del árbol binario se denomina nodo raíz. Cada nodo principal puede tener como máximo 2 nodos secundarios, que son el nodo secundario izquierdo y el nodo secundario derecho.
Un nodo en un árbol binario tiene tres campos:
- Elemento de datos: almacena el valor de los datos que debe almacenar el nodo.
- Puntero al nodo secundario izquierdo: almacena la referencia (o dirección) al nodo secundario izquierdo.
- Puntero al nodo secundario derecho: almacena la referencia al nodo secundario derecho.
De esta forma, varios nodos se combinan para construir un árbol binario.
Un árbol binario se puede representar como:
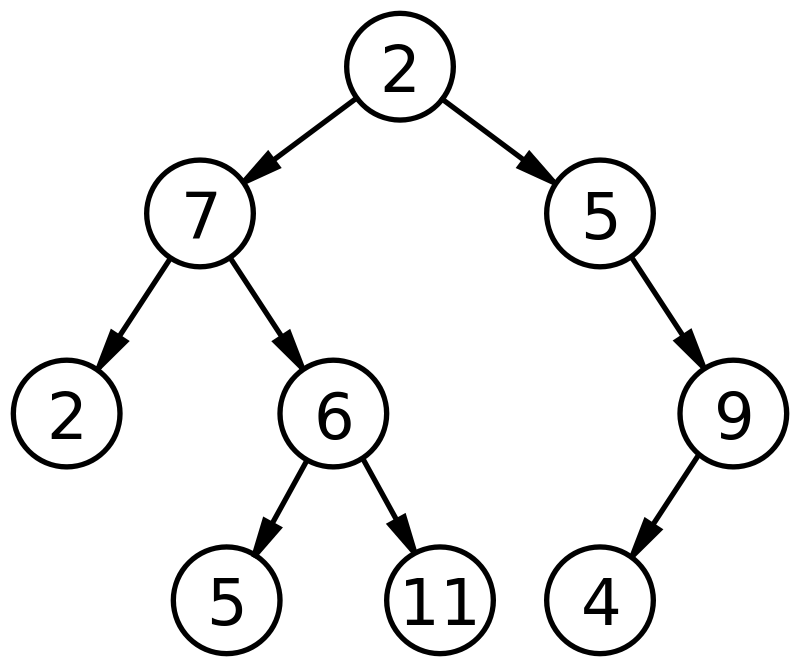
Fuente
De la figura anterior, el nodo raíz 2 tiene dos hijos (o nodos hijos), 7 y 5. 7 se denomina nodo hijo izquierdo y 5 se denomina nodo hijo derecho. De esta forma, cada uno de los nodos secundarios actúa como un nodo principal para varios otros nodos y juntos representan el árbol binario.
Echa un vistazo a: Tipos de árbol binario
Terminologías utilizadas en Binary Tree
Nodo : La representación básica de un punto de terminación en un árbol.
Nodo raíz : el nodo superior de un árbol binario.
Nodo principal: si un nodo está conectado a otro nodo a través de los bordes, se conoce como nodo principal. En un árbol binario, un nodo principal puede tener un máximo de 2 nodos secundarios.
Nodo secundario: si un nodo tiene un predecesor, se lo conoce como nodo secundario.
Nodo hoja : un nodo que no tiene ningún nodo secundario se denomina nodo hoja.
Profundidad de un nodo : Es la distancia desde el nodo raíz hasta ese nodo en particular cuya profundidad se va a medir.
Altura del árbol : Es la distancia más larga desde el nodo raíz hasta el nodo hoja.
Estas son algunas terminologías básicas de un árbol binario. Con esta comprensión básica de un árbol binario, pasemos a un avance del árbol binario conocido como árbol de búsqueda binaria.
Lea también: Algoritmo de búsqueda binaria: función, beneficios, complejidad de tiempo y espacio
¿Qué es un árbol de búsqueda binaria?
Como sugiere el nombre, un árbol de búsqueda binaria o BST es un árbol que se utiliza para clasificar, recuperar y buscar datos. También es un tipo de estructura de datos no lineal en la que los nodos se organizan en un orden particular. Por lo tanto, también se denomina " Árbol binario ordenado ". Tiene las siguientes propiedades:
- El subárbol izquierdo de un nodo tiene nodos que son solo menores que la clave de ese nodo.
- El subárbol derecho de un nodo tiene nodos que son solo mayores que la clave de ese nodo.
- Cada nodo tiene claves distintas y no se permiten duplicados en el árbol de búsqueda binaria.
- El subárbol izquierdo y derecho también debe ser un árbol de búsqueda binaria.
Visualicemos este concepto para obtener una comprensión clara de los árboles de búsqueda binarios.
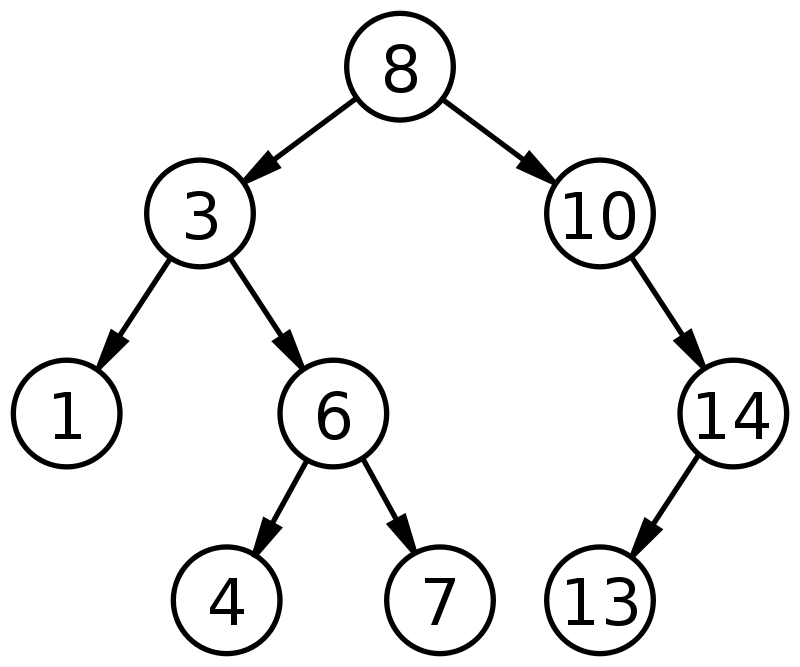
Fuente
En la figura anterior, vemos que el valor del nodo raíz es 8. Con un examen más detallado, se observa que todos los valores en el subárbol izquierdo son menores que el valor del nodo raíz y todos los valores en el subárbol derecho tienen valores que son mayores que el nodo raíz. Además, se observa que cada valor en el árbol de búsqueda binaria es único y no hay duplicados. Por lo tanto, se verifican las propiedades del árbol de búsqueda binaria indicadas anteriormente.
En otro ejemplo más, vemos que los subárboles izquierdo y derecho son árboles de búsqueda binarios con valores únicos en todo el árbol. El valor en el nodo de hoja en el subárbol izquierdo es 12, que es mayor que el valor del nodo raíz, que es 12. Por lo tanto, esto no satisface la propiedad de BST y, por lo tanto, no es un árbol de búsqueda binario.
Operación de búsqueda en un BST –
Considere un árbol de búsqueda binario con los valores que se indican a continuación. Entendamos cómo se realiza la operación de búsqueda para obtener 9 del árbol de búsqueda binaria.

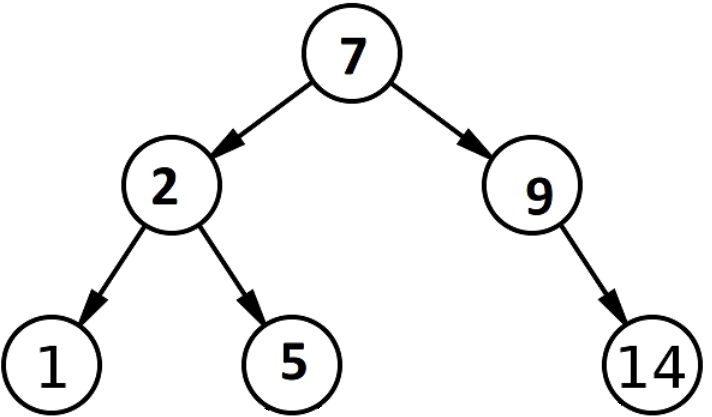
Fuente
Para realizar la búsqueda binaria, primero ordenaremos todos los enteros en una matriz ordenada. Esto se llama como el espacio de búsqueda. Este espacio de búsqueda constará de dos punteros, denominados punteros de inicio y fin. La matriz del árbol de búsqueda binario anterior se representa como:
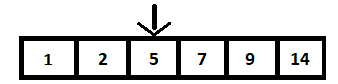
El primer paso es calcular el valor medio de la matriz y compararlo con el valor que se va a buscar, 9 en nuestro caso. Esto se hace calculando n/2, donde n es el número total de elementos en la matriz (BST) y es 6. Por lo tanto, el tercer elemento es el elemento del medio que es 5.
Ahora que el elemento del medio se compara con 9 y como no es igual (mayor), la operación de búsqueda se realizará en la matriz derecha. De esta forma, la operación de búsqueda se reduce a la mitad, como se muestra a continuación:
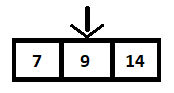
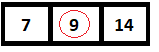
En el siguiente paso, se calcula el elemento del medio y se encuentra que es 9, que coincide con nuestro elemento a buscar.
Árbol binario vs Árbol de búsqueda binario –
Ahora que tenemos una comprensión básica tanto del árbol binario como de los árboles binarios de búsqueda, resumamos rápidamente algunas de las diferencias entre ambos.
| Base de comparación | Árbol binario | Árbol de búsqueda binaria |
| Definición | Un árbol binario es una estructura de datos no lineal en la que un nodo puede tener 0, 1 o 2 nodos. Individualmente, cada nodo consta de un puntero izquierdo, un puntero derecho y un elemento de datos. | Un árbol de búsqueda binario es un árbol binario organizado con una organización estructurada de nodos. Cada subárbol también debe ser de esa estructura particular. |
| Estructura | No hay una estructura de organización requerida de los nodos en el árbol. | Los valores del subárbol izquierdo de un nodo en particular deben ser menores que ese nodo y los valores del subárbol derecho deben ser mayores. |
| Operaciones Realizadas | Las operaciones que se pueden realizar son el borrado, la inserción y el recorrido. | Como se trata de árboles binarios ordenados, se utilizan para la búsqueda, inserción y eliminación binaria rápida y eficiente. |
| Tipos | Hay varios tipos. Los más comunes son el árbol binario completo, el árbol binario completo y el árbol binario extendido. | Los más populares son AVL Trees, Splay Trees, Tango Trees, T-Trees. |
Conclusión
Por lo tanto, inferimos que aunque tanto el Árbol binario como el Árbol de búsqueda binario tienen una estructura jerárquica común con una colección de nodos, tienen varias diferencias en su aplicación. Un árbol binario es una estructura básica con una regla simple que ningún padre debe tener más de 2 hijos, mientras que el árbol binario de búsqueda es una variante del árbol binario que sigue un orden particular con el que se deben organizar los nodos.
Si tiene curiosidad por conocer el árbol binario frente al árbol de búsqueda binario, consulte el Diploma PG en ciencia de datos de IIIT-B y upGrad, creado para profesionales que trabajan y ofrece más de 10 estudios de casos y proyectos, talleres prácticos prácticos, tutoría con la industria. expertos, 1 a 1 con mentores de la industria, más de 400 horas de aprendizaje y asistencia laboral con las mejores empresas.
Aprenda cursos de ciencia de datos en línea de las mejores universidades del mundo. Obtenga programas Executive PG, programas de certificados avanzados o programas de maestría para acelerar su carrera.
¿Cómo podemos recorrer un árbol de búsqueda binario?
A diferencia de las estructuras de datos lineales como matrices, listas vinculadas, pilas y colas, en las que podemos recorrer la estructura de datos de una sola manera, un árbol de búsqueda binario nos da la libertad de recorrerla de múltiples maneras. Los recorridos de árbol más populares son los siguientes: En un recorrido en orden, primero recorremos el nodo izquierdo del árbol, luego el nodo raíz del árbol y finalmente el nodo derecho del árbol. También seguimos la misma moda en todos los subárboles. En un recorrido de preorden, primero recorremos el nodo raíz del árbol y luego el nodo izquierdo y derecho respectivamente. También seguimos la misma moda en todos los subárboles. En un recorrido posterior al orden, primero recorremos el nodo izquierdo y derecho del árbol respectivamente, y finalmente el nodo raíz del árbol. También seguimos la misma moda en todos los subárboles.
¿Cuáles son las ventajas y desventajas de un BST?
Las siguientes son las ventajas y desventajas de un árbol de búsqueda binario. Las ventajas son: operaciones como inserción, eliminación y búsqueda se pueden realizar en tiempo O (log n), donde n es el número de nodos. Todos los elementos en un BST están ordenados para que podamos atravesar fácilmente un BST simplemente usando el recorrido en orden. BST se puede usar de manera eficiente para diseñar asignadores de memoria para acelerar el proceso de búsqueda de bloques de memoria. La mayor desventaja de un árbol de búsqueda binario es que siempre debemos usar un BST balanceado como AVL y Red-Black Tree porque si no usamos un BST balanceado, las operaciones de nuestro árbol no se realizarán en tiempo logarítmico.
Diferenciar entre un árbol binario completo y un árbol binario completo.
Un árbol binario completo es un árbol binario en el que todos los nodos tienen nodos secundarios entre 0 y 2. En otras palabras, un árbol binario en el que todos los nodos tienen al menos 2 nodos secundarios excepto los nodos hoja se conoce como árbol binario completo. Por otro lado, un árbol binario completo es un árbol binario donde cada nodo está completamente lleno (exactamente dos nodos secundarios) y los nodos hoja se ubican lo más a la izquierda posible.
