Ejemplo de red bayesiana [con representación gráfica]

Introducción

En estadística, los modelos probabilísticos se utilizan para definir una relación entre variables y se pueden utilizar para calcular las probabilidades de cada variable. En muchos problemas, hay un gran número de variables. En tales casos, los modelos completamente condicionales requieren una gran cantidad de datos para cubrir todos y cada uno de los casos de las funciones de probabilidad que pueden ser difíciles de calcular en tiempo real. Ha habido varios intentos de simplificar los cálculos de probabilidad condicional, como Naive Bayes, pero aún así, no ha demostrado ser eficiente ya que reduce drásticamente varias variables.

La única forma es desarrollar un modelo que pueda preservar las dependencias condicionales entre variables aleatorias y la independencia condicional en otros casos. Esto nos lleva al concepto de Redes Bayesianas. Estas Redes Bayesianas nos ayudan a visualizar efectivamente el modelo probabilístico para cada dominio y a estudiar la relación entre variables aleatorias en forma de un gráfico fácil de usar.

Aprenda el curso ML de las mejores universidades del mundo. Obtenga programas de maestría, PGP ejecutivo o certificado avanzado para acelerar su carrera.

¿Qué son las Redes Bayesianas?

Por definición, las redes bayesianas son un tipo de modelo gráfico probabilístico que utiliza las inferencias bayesianas para los cálculos de probabilidad. Representa un conjunto de variables y sus probabilidades condicionales con un gráfico acíclico dirigido (DAG). Son principalmente adecuados para considerar un evento que ha ocurrido y predecir la probabilidad de que cualquiera de las varias causas posibles conocidas sea el factor contribuyente.

Fuente

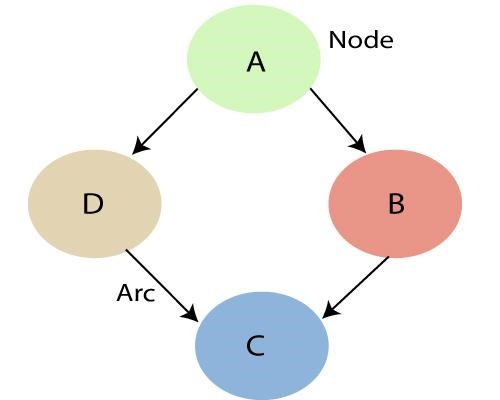
Como se mencionó anteriormente, haciendo uso de las relaciones que especifica la Red Bayesiana, podemos obtener la Distribución de Probabilidad Conjunta (JPF) con las probabilidades condicionales. Cada nodo del gráfico representa una variable aleatoria y el arco (o flecha dirigida) representa la relación entre los nodos. Pueden ser de naturaleza continua o discreta.

En el diagrama anterior, A, B, C y D son 4 variables aleatorias representadas por nodos dados en la red del gráfico. Para el nodo B, A es su nodo padre y C es su nodo hijo. El nodo C es independiente del nodo A.

Antes de entrar en la implementación de una red bayesiana, hay algunos conceptos básicos de probabilidad que deben entenderse.

Propiedad local de Markov

Las Redes Bayesianas satisfacen la propiedad conocida como Propiedad Local de Markov. Establece que un nodo es condicionalmente independiente de sus no descendientes, dados sus padres. En el ejemplo anterior, P(D|A, B) es igual a P(D|A) porque D es independiente de su no descendiente, B. Esta propiedad nos ayuda a simplificar la distribución conjunta. La propiedad local de Markov nos lleva al concepto de un campo aleatorio de Markov, que es un campo aleatorio alrededor de una variable que se dice que sigue las propiedades de Markov.

La probabilidad condicional

En matemáticas, la probabilidad condicional del evento A es la probabilidad de que ocurra el evento A dado que ya ocurrió otro evento B. En términos simples, p(A | B) es la probabilidad de que ocurra el evento A, dado que ocurre el evento B. Sin embargo, hay dos tipos de posibilidades de eventos entre A y B. Pueden ser eventos dependientes o eventos independientes. Dependiendo de su tipo, hay dos formas diferentes de calcular la probabilidad condicional.

• Dado que A y B son eventos dependientes, la probabilidad condicional se calcula como P (A| B) = P (A y B) / P (B)
• Si A y B son eventos independientes, entonces la expresión de la probabilidad condicional viene dada por P(A| B) = P (A)

Distribución de probabilidad conjunta

Antes de entrar en un ejemplo de Redes Bayesianas, comprendamos el concepto de Distribución de Probabilidad Conjunta. Considere 3 variables a1, a2 y a3. Por definición, las probabilidades de todas las diferentes combinaciones posibles de a1, a2 y a3 se denominan distribución de probabilidad conjunta.

Si P[a1,a2, a3,….., an] es el JPD de las siguientes variables de a1 a an, entonces hay varias formas de calcular la Distribución de Probabilidad Conjunta como una combinación de varios términos tales como,

P[a1,a2, a3,….., an] = P[a1 | a2, a3,….., an] * P[a2, a3,….., an]

= P[a1 | a2, a3,….., an] * P[a2 | a3,….., an]….P[an-1|an] * P[an]

Generalizando la ecuación anterior, podemos escribir la distribución de probabilidad conjunta como,

P(X i |X i-1 ,………, X n ) = P(X i |Padres(X i ))

Ejemplo de Redes Bayesianas

Comprendamos ahora el mecanismo de las redes bayesianas y sus ventajas con la ayuda de un ejemplo simple. En este ejemplo, imaginemos que se nos da la tarea de modelar las notas de un estudiante ( m ) para un examen que acaba de dar. A partir del gráfico de red bayesiano dado a continuación, vemos que las marcas dependen de otras dos variables. Ellos son,

• Nivel del examen ( e )– Esta variable discreta denota la dificultad del examen y tiene dos valores (0 para fácil y 1 para difícil)
• Nivel de coeficiente intelectual ( i ): representa el nivel de cociente de inteligencia del estudiante y también es de naturaleza discreta y tiene dos valores (0 para bajo y 1 para alto)

Adicionalmente, el nivel de CI del alumno también nos lleva a otra variable, que es el Puntaje de Aptitud del (de los) alumno( s ). Ahora, con las notas que el estudiante ha obtenido, puede asegurar la admisión a una universidad en particular. La distribución de probabilidad para ser admitido ( a ) en una universidad también se muestra a continuación.

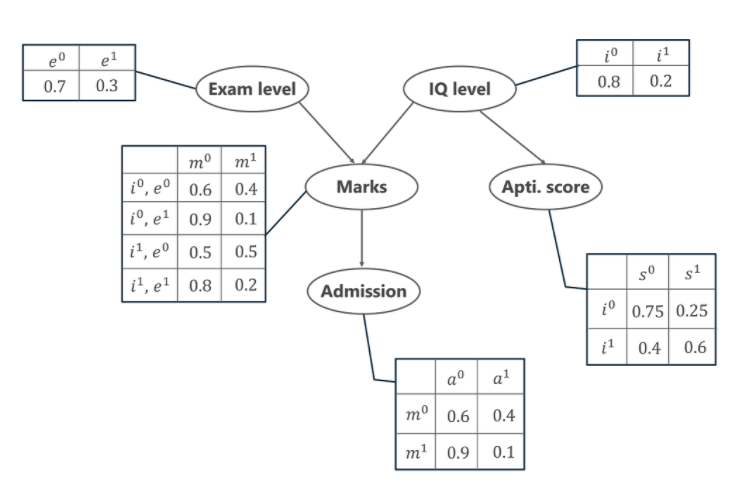
En el gráfico anterior, vemos varias tablas que representan los valores de distribución de probabilidad de las 5 variables dadas. Estas tablas se llaman Tabla de Probabilidades Condicionales o CPT. Hay algunas propiedades del CPT que se detallan a continuación:

• La suma de los valores de CPT en cada fila debe ser igual a 1 porque todos los casos posibles para una variable en particular son exhaustivos (representando todas las posibilidades).
• Si una variable que es de naturaleza booleana tiene k padres booleanos, entonces en el CPT tiene valores de probabilidad de 2K.

Volviendo a nuestro problema, enumeremos primero todos los eventos posibles que ocurren en la tabla anterior.

1. Nivel de examen (e)
2. Nivel de CI (i)
3. Puntaje de Aptitud (s)
4. Marcas (m)
5. Admisión (a)

Estas cinco variables se representan en forma de Gráfico Acíclico Dirigido (DAG) en un formato de Red Bayesiana con sus tablas de Probabilidad Condicional. Ahora, para calcular la Distribución de Probabilidad Conjunta de las 5 variables la fórmula viene dada por,

PAG[a, metro, yo, mi, s]= PAG(a | metro) . P(m | yo, mi) . Pi) . Educación física) . P(s | yo)

De la fórmula anterior,

• P(a | m) denota la probabilidad condicional de que el estudiante obtenga la admisión en función de las calificaciones que obtuvo en el examen.
• P(m | i, e) representa las notas que obtendrá el estudiante dado su nivel de CI y la dificultad del Nivel del examen.
• P(i) y P(e) representan la probabilidad del nivel de CI y el nivel del examen.
• P(s | i) es la probabilidad condicional del puntaje de aptitud del estudiante, dado su nivel de CI.

Con las siguientes probabilidades calculadas, podemos encontrar la Distribución de Probabilidad Conjunta de toda la Red Bayesiana.

Cálculo de la Distribución de Probabilidad Conjunta

Calculemos ahora el JPD para dos casos.

Caso 1: Calcular la probabilidad de que a pesar de que el nivel del examen sea difícil, el estudiante con un coeficiente intelectual bajo y un puntaje de aptitud bajo logre aprobar el examen y asegurar la admisión a la universidad.

A partir de la declaración del problema verbal anterior, la distribución de probabilidad conjunta se puede escribir de la siguiente manera,

P[a=1, m=1, i=0, e=1, s=0]

De las tablas de probabilidad condicional anteriores, los valores para las condiciones dadas se alimentan a la fórmula y se calculan de la siguiente manera.

PAG[a=1, m=1, i=0, e=0, s=0] = PAG(a=1 | m=1) . PAGS(m=1 | i=0, e=1) . P(i=0) . P(e=1) . P(s=0 | i=0)

= 0,1 * 0,1 * 0,8 * 0,3 * 0,75

= 0.0018

Caso 2: En otro caso, calcule la probabilidad de que el estudiante tenga un nivel de CI alto y un puntaje de aptitud, el examen es fácil pero no lo aprueba y no asegura la admisión a la universidad.

La fórmula para el JPD está dada por

P[a=0, m=0, i=1, e=0, s=1]

Por lo tanto,

PAG[a=0, m=0, i=1, e=0, s=1]= PAG(a=0 | m=0) . PAGS(m=0 | i=1, e=0) . P(i=1) . P(e=0) . P(s=1 | i=1)

= 0,6 * 0,5 * 0,2 * 0,7 * 0,6

= 0.0252

Por lo tanto, de esta manera, podemos hacer uso de redes bayesianas y tablas de probabilidad para calcular la probabilidad de que ocurran varios eventos posibles.

Lea también: Ideas y temas de proyectos de aprendizaje automático

Conclusión

Existen innumerables aplicaciones para las redes bayesianas en filtrado de spam, búsqueda semántica, recuperación de información y muchas más. Por ejemplo, con un síntoma dado podemos predecir la probabilidad de que ocurra una enfermedad con varios otros factores que contribuyen a la enfermedad. Por lo tanto, el concepto de red bayesiana se presenta en este artículo junto con su implementación con un ejemplo de la vida real.

Si tiene curiosidad por dominar el aprendizaje automático y la IA, impulse su carrera con un curso avanzado sobre aprendizaje automático e IA con IIIT-B y la Universidad John Moores de Liverpool.