ベイジアンシンキングとは何ですか？ はじめにと定理

1700年代に英国の統計学者で哲学者のトーマスベイズによって与えられた統計定理は、世界中の科学者やアナリストの指針であり続けています。 今日、ベイズの考え方は、医学、科学、技術、およびその他のいくつかの分野で応用されており、私たちの世界観とその結果としての行動に強く影響を与え続けています。

トーマス・ベイズのアイデアは驚くほど単純でした。 ベイズによれば、仮説が真である確率は、2つの条件に依存します。それは、私たちがすでに知っていること（事前の知識）に基づいてどれだけ合理的であるか、そしてそれが新しい証拠にどれだけうまく適合するかです。 したがって、ベイズの考え方は、結論にジャンプする前に前者が事前の知識を含むという点で、従来の仮説検定とは異なります。

予備的な紹介を念頭に置いて、ベイズ統計についてもう少し詳しく見ていきましょう。

ベイズ統計

簡単に言えば、ベイズ統計は確率を統計問題に適用して、新しいデータの証拠に照らして以前の信念を更新します。 確率は、特定のイベントに対する信念の程度を表します。

信念の程度は、個人的な仮定または以前の実験の結果に基づくイベントに関する以前の知識に基づく場合があります。 ベイズ統計は、ベイズの定理を使用して確率を計算します。 次に、ベイズの定理は、イベントに関連する新しい証拠と事前情報に基づいて、イベントの条件付き確率を記述します。

そのことを念頭に置いて、ベイズの定理を深く理解する前に、条件付き確率の基本的な概念をブラッシュアップしましょう。

条件付き確率

条件付き確率は、前のイベントまたは結果の発生に基づくイベントまたは結果の可能性として定義できます。 これは、前のイベントの確率に次のイベントまたは条件付きイベントの確率を掛けることによって計算されます。

概念をよりよく理解するために例を見てみましょう。

• イベントAは、外出を計画している家族がピクニックに行くことです。 家族がピクニックに行く可能性は80％です。
• イベントBは、家族がピクニックに出かける日に雨が降るというものです。 天気予報によると、ピクニックの日に降水確率は60％です。
• したがって、家族がピクニックに出て雨が降る確率（P）は、次のように計算されます。

P（ピクニックと雨）= P（雨|ピクニック）P（ピクニック）=（0.60）*（0.80）= 0.48

上記の例では、条件付き確率は、2つのイベントAとBを相互に関連させて調べます。つまり、家族がピクニックに行き、同じ日に雨が降る確率です。

したがって、条件付き確率は無条件確率とは異なります。無条件確率とは、他の1つまたは複数のイベントが発生したかどうか、または他の条件が存在するかどうかに関係なく、イベントが発生する可能性を指すためです。

条件付き確率の式

条件付き確率の式は、確率の乗法則に基づいています。

P（AおよびB）またはP（AUB）= P（Aが与えられたB）またはP（B | A）* P（A）

上記の式で、P（AとB）は同時確率であり、2つ以上のイベントが同時に発生する可能性を指します。 P（A、B）とも表記されます。

確率の乗法から条件付き確率方程式を推定する方法は次のとおりです。

ステップ1：乗算規則を書き留めます。

P（AおよびB）= P（B | A）* P（A）

ステップ2：方程式の両辺をP（A）で割ります。

P（AおよびB）/ P（A）= P（B | A）* P（A）/ P（A）

ステップ3：方程式の右辺のP（A）をキャンセルします。

P（AおよびB）/ P（A）= P（B | A）

ステップ4：方程式を書き直します。

P（AおよびB）= P（B | A）/ P（A）

したがって、条件付き確率の式は次のように与えられます。

P（AおよびB）= P（B | A）/ P（A）

ベイズの定理

ベイズの定理を使用して、新しい関連する証拠に基づいて信念と信念を更新できます。 たとえば、特定の人が癌を患っている確率を把握しようとしている場合、一般的には、癌を患っている人口の割合であると想定します。 ただし、問題の人物が通常の喫煙者であるなどの追加の証拠を導入すると、個人が喫煙者である場合に癌になる可能性が高くなるため、認識（したがって確率）を更新できます。 したがって、事前の知識と追加の証拠の両方を利用して、見積もりを改善します。

ベイズの定理の公式

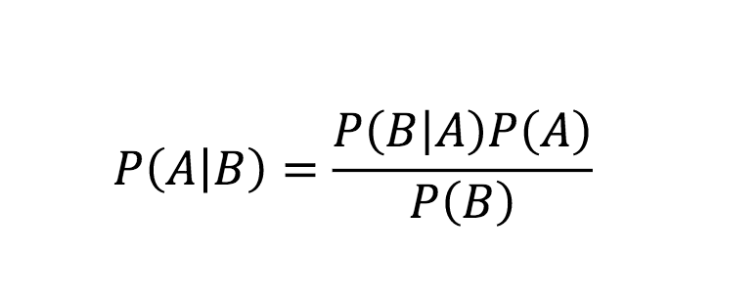
ソース

上記の式はベイズの法則です。 ここで、ベイズの定理方程式の段階的な導出について見ていきましょう。

ステップ1： AとBの2つのイベントについて考えます。Aは確率を計算したいイベントであり、BはAに関連する追加の証拠です。

ステップ2：イベントAとBの同時確率と条件付き確率の関係を書き留めます。

P（A、B）= P（A | B）* P（B）= P（B、A）= P（B | A）* P（A）

ステップ3： 2つの条件付き確率項を互いに等しく設定します。

P（A | B）* P（B）= P（B | A）* P（A）

ステップ4：方程式の両辺をP（B）で割ります。

P（A | B）* P（B）/ P（B）= P（B | A）* P（A）/ P（B）

ステップ5：方程式の左側のP（B）をキャンセルします。

P（A | B）= P（B | A）* P（A）/ P（B）

したがって、ベイズの定理の式は次のようになります。

P（A | B）= P（B | A）* P（A）/ P（B）

ベイズの定理方程式の用語を理解する

P（A | B）= P（B | A）* P（A）/ P（B）

• P（A | B）は、事後確率または推定しようとしている確率と呼ばれます。 前の例に基づくと、事後確率は、その人が通常の喫煙者であるとすると、その人が癌を患っている確率になります。
• P（B | A）は尤度と呼ばれ、最初の仮説を前提として、追加の証拠を検出する確率を指します。 上記の例では、可能性は、その人が癌を患っていることを前提として、その人が喫煙者である確率です。
• P（A）は、事前確率、または追加の証拠や情報がない場合の仮説の確率です。 上記の例では、事前確率は癌を患う確率です。
• P（B）は、証拠を観察する周辺尤度または全確率です。 上記の例のコンテキストでは、周辺尤度は喫煙者である確率です。

ベイズの定理を理解するための簡単な例

前の例のいくつかの架空の数値を使用して、ベイズの定理を適用した場合の効果を確認します。

癌になる確率が0.06であると仮定します。つまり、6％の人が癌を患っています。 ここで、喫煙者である確率が0.20であるとすると、20％の人が喫煙者であり、癌のある人の30％が喫煙者です。 したがって、P（喫煙者|がん）=0.30です。

当初、癌になる確率は単純に0.06（以前）です。 しかし、新しい証拠を使用して、P（Cancer | Smoker）= P（（Smoker | Cancer）* P（Cancer））/ P（Smoker）=（0.30 * 0.06）/（0.20）=0.09を計算できます。

世界のトップ大学からオンラインでデータサイエンスコースを学びましょう。 エグゼクティブPGプログラム、高度な証明書プログラム、または修士プログラムを取得して、キャリアを早急に進めましょう。

今後の方向性：データサイエンスまたは機械学習のキャリアのための統計の概念を習得する

upGradのより高度なEdTech学習プラットフォームは、その豊富なコースと没入型学習体験により、世界中の50万人を超える専門家に影響を与えてきました。 85か国以上に40,000以上の学習者がいるため、upGradの業界関連のコースは、選択した分野でのキャリアを向上させることが保証されています。

データサイエンスの科学のマスターは、統計、予測分析、機械学習、ビッグデータ分析、データ視覚化などの主要なスキルを与える18か月のコースです。

プログラムのハイライト：

• リバプールジョンムーア大学の修士号とIIITバンガロアのエグゼクティブPGP
• 500時間以上のコンテンツ、60以上のケーススタディとプロジェクト、20以上のライブセッション、14以上のプログラミング言語とツール
• 業界ネットワーキング、疑問解決セッション、および学習サポート

機械学習とディープラーニングの高度な証明書プログラムは、ピアネットワーキングの機会、実践的なプロジェクト、業界のメンターシップ、および360度のキャリア支援を備えた厳格な6か月のコースです。

プログラムのハイライト：

• IIITバンガロアからの名誉ある認識
• 240時間以上のコンテンツ、5つ以上のケーススタディ、プロジェクト、24時間以上のライブセッション、12のプログラミング言語、ツール、ライブラリのカバレッジ
• 1：8のグループコーチングセッションと業界の専門家との1：1のメンターシップセッション

結論

ベイジアン思考は、私たちのほとんどがそれに気づいていないにもかかわらず、人間の思考、探究、信念のいくつかの領域を支えています。 がん検診や地球温暖化から金融政策やリスク評価や保険に至るまで、ベイズの考え方は基本です。 有名な英国の数学者アランチューリングでさえ、第二次世界大戦中にドイツのエニグマコードを解読するためにベイズアプローチを採用したと考えられています。

upGradにサインアップして、主要な統計概念などの知識を深めてください。