多項式回帰：重要性、段階的な実装

公開: 2021-01-29

序章

機械学習のこの広大な分野で、私たちのほとんどが研究したであろう最初のアルゴリズムは何でしょうか？はい、それは線形回帰です。ほとんどの場合、機械学習プログラミングの初期の頃に学んだ最初のプログラムとアルゴリズムである線形回帰には、線形タイプのデータを使用した独自の重要性と能力があります。

遭遇したデータセットが線形分離可能でない場合はどうなりますか？線形回帰モデルが独立変数と従属変数の両方の間に何らかの関係を導き出すことができない場合はどうなりますか？

多項式回帰として知られる別のタイプの回帰があります。その名の通り、多項式回帰は、従属（y）変数と独立変数（x）の間の関係をn次多項式としてモデル化する回帰アルゴリズムです。この記事では、Pythonでの実装とともに、多項式回帰の背後にあるアルゴリズムと数学を理解します。

多項式回帰とは何ですか？

前に定義したように、多項式回帰は線形回帰の特殊なケースであり、指定された（n）次数の多項式が、従属変数と独立変数の間に曲線関係を形成する非線形データに適合します。

y = b 0 + b 1 x 1 + b 2 x 1 2 + b 3 x 13 + …… bnx 1 n

ここ、

yは従属変数（出力変数）です

x1は独立変数（予測変数）です

b0はバイアスです

b 1 、b 2 、….b nは、回帰方程式の重みです。

多項式の次数（ n ）が高くなると、多項式はより複雑になり、モデルがオーバーフィットする可能性があります。これについては、後の部分で説明します。

回帰方程式の比較

単純な線形回帰===>y= b0 + b1x

重回帰===>y= b0 + b1x1 + b2x2 +b3x3+……bnxn

多項式回帰===>y= b0 + b1x1 + b2x12 +b3x13+……bnx1n

上記の3つの方程式から、それらにはいくつかの微妙な違いがあることがわかります。単純および重回帰は、次数が1しかないという点で、多項式回帰方程式とは異なります。重回帰は、いくつかの変数x1、x2などで構成されます。多項式回帰方程式には変数x1が1つしかありませんが、他の2つと区別する次数nがあります。

多項式回帰の必要性

以下の図から、最初の図では、与えられた非線形データポイントのセットに線形線を当てはめようとしていることがわかります。直線がこの非線形データと関係を形成することは非常に困難になることが理解されます。このため、モデルをトレーニングすると、損失関数が増加し、高いエラーが発生します。

一方、多項式回帰を適用すると、線がデータポイントにうまく適合していることがはっきりとわかります。これは、データポイントに適合する多項式が、データセット内の変数間に何らかの関係を導き出すことを意味します。したがって、データポイントが非線形に配置されている場合は、多項式回帰モデルが必要です。

Pythonでの多項式回帰の実装

ここから、多項式回帰を実装するPythonで機械学習モデルを構築します。線形回帰と多項式回帰で得られた結果を比較します。まず、多項式回帰で解決しようとしている問題を理解しましょう。

問題の説明

ここでは、企業から複数の候補者を雇おうとしている新興企業の場合を考えてみましょう。会社のさまざまな職務にさまざまな開口部があります。スタートアップには、前の会社の各役割の給与の詳細があります。したがって、候補者が以前の給与について言及する場合、スタートアップのHRは既存のデータでそれを検証する必要があります。したがって、PositionとLevelという2つの独立変数があります。従属変数（出力）は、多項式回帰を使用して予測される給与です。

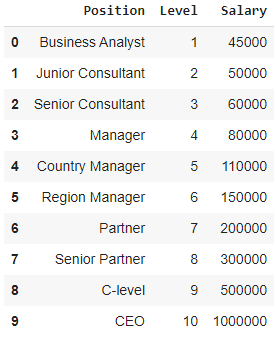
上記の表をグラフで視覚化すると、データが本質的に非線形であることがわかります。つまり、レベルが上がると給与も高くなり、下図のような曲線になります。

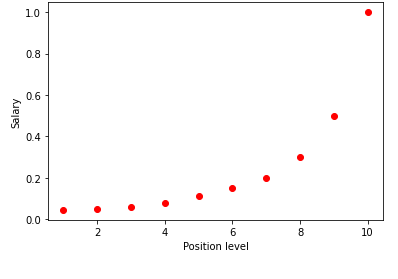
ステップ1：データの前処理機械学習モデルを構築する最初のステップは、ライブラリをインポートすることです。ここでは、インポートする基本ライブラリは3つだけです。この後、データセットがGitHubリポジトリからインポートされ、従属変数と独立変数が割り当てられます。独立変数は変数Xに格納され、従属変数は変数yに格納されます。
numpyをnpとしてインポートします
matplotlib.pyplotをpltとしてインポートします
パンダをpdとしてインポートします

データセット=pd.read_csv（'https://raw.githubusercontent.com/mk-gurucharan/Regression/master/PositionSalaries_Data.csv'）
X =dataset.iloc [:, 1：-1] .values
y = dataset.iloc [：、-1] .values
ここで、[：、1：-1]という用語では、最初のコロンはすべての行を取得する必要があることを表し、1：-1という用語は、含まれる列が最初の列から最後から2番目の列までであることを示します。 -1。
ステップ2：線形回帰モデル次のステップでは、多重線形回帰モデルを作成し、それを使用して独立変数から給与データを予測します。このため、LinearRegressionクラスはsklearnライブラリからインポートされます。次に、トレーニングの目的で変数Xとyに適合します。

sklearn.linear_modelからimportLinearRegression
regressor = LinearRegression（）
regressor.fit（X、y）
モデルが構築されると、結果を視覚化すると、次のグラフが得られます。
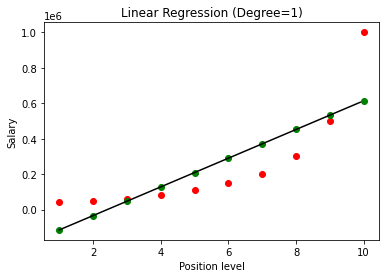
はっきりとわかるように、非線形データセットに直線を当てはめることによって、機械学習モデルによって導出される関係はありません。したがって、変数間の関係を取得するには、多項式回帰を実行する必要があります。
ステップ3：多項式回帰モデルこの次のステップでは、このデータセットに多項式回帰モデルを適合させ、結果を視覚化します。このために、PolynomialFeaturesという名前のsklearnモジュールから別のクラスをインポートします。このクラスでは、構築する多項式の次数を指定します。次に、LinearRegressionクラスを使用して、多項式をデータセットに適合させます。

sklearn.preprocessingからimportPolynomialFeatures
sklearn.linear_modelからimportLinearRegression
poly_reg = PolynomialFeatures（degree = 2）
X_poly = poly_reg.fit_transform（X）
lin_reg = LinearRegression（）
lin_reg.fit（X_poly、y）
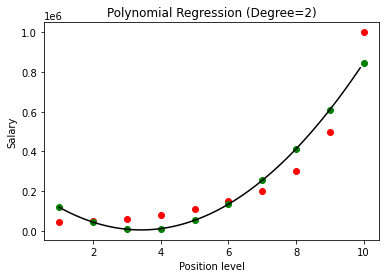
上記の場合、多項式の次数を2に等しくしました。グラフをプロットすると、導出されたある種の曲線がありますが、それでも実際のデータ（赤）からの偏差が大きいことがわかります。）および予測された曲線ポイント（緑色）。したがって、次のステップでは、多項式の次数を3や4などのより高い数値に増やしてから、互いに比較します。

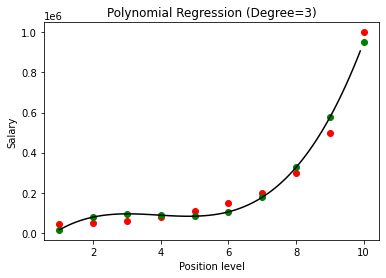
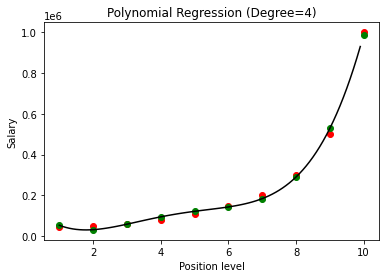
多項式回帰の結果を次数3および4と比較すると、次数が増加するにつれて、モデルはデータとうまく一致することがわかります。したがって、次数が高いほど、多項式がトレーニングデータにより正確に適合することが可能になると推測できます。ただし、これは過剰適合の完璧なケースです。したがって、過剰適合を防ぐために、nの値を正確に選択することが重要になります。
過剰適合とは何ですか？
名前が示すように、過剰適合は、関数（またはこの場合は機械学習モデル）が限られたデータポイントのセットにあまりにも密接に適合している場合の統計の状況と呼ばれます。これにより、新しいデータポイントで関数のパフォーマンスが低下します。

機械学習では、モデルが特定のトレーニングデータポイントのセットに過剰適合していると言われる場合、同じモデルが完全に新しいポイントのセット（テストデータセットなど）に導入されると、モデルのパフォーマンスが非常に悪くなります。過剰適合モデルはデータで十分に一般化されておらず、トレーニングデータポイントでのみ過剰適合しています。
多項式回帰では、多項式の次数が増加するにつれて、モデルがトレーニングデータに過剰適合する可能性が高くなります。上記の例では、次数の最適値を選択するための試行錯誤の基準でのみ修正できる、多項式回帰での過剰適合の典型的なケースが見られます。
また読む：機械学習プロジェクトのアイデア
結論
結論として、多項式回帰は、従属変数と独立変数の間に非線形の関係がある多くの状況で利用されます。このアルゴリズムは外れ値に対する感度に悩まされていますが、回帰直線を当てはめる前に外れ値を処理することで修正できます。したがって、この記事では、単純なデータセットでのPythonプログラミングでの実装例とともに、多項式回帰の概念を紹介しました。
機械学習について詳しく知りたい場合は、IIIT-BとupGradの機械学習とAIのPGディプロマをご覧ください。これは、働く専門家向けに設計されており、450時間以上の厳格なトレーニング、30以上のケーススタディと課題、IIIT-を提供します。 B卒業生のステータス、5つ以上の実践的なキャップストーンプロジェクト、トップ企業との仕事の支援。
世界のトップ大学からMLコースを学びましょう。マスター、エグゼクティブPGP、または高度な証明書プログラムを取得して、キャリアを迅速に追跡します。
線形回帰とはどういう意味ですか？
線形回帰は、従属変数の助けを借りて未知の変数の値を見つけることができる一種の予測数値分析です。また、1つの従属変数と1つ以上の独立変数の間の関係についても説明します。線形回帰は、2つの変数間のリンクを示すための統計的手法です。線形回帰は、データポイントのセットから傾向線をプロットします。線形回帰を使用して、癌の診断や株価など、一見ランダムなデータから予測モデルを生成できます。線形回帰を計算する方法はいくつかあります。データ内の未知の変数を推定し、データポイントと傾向線の間の垂直距離の合計に視覚的に変換する通常の最小二乗アプローチは、最も一般的なアプローチの1つです。
線形回帰の欠点にはどのようなものがありますか？
ほとんどの場合、回帰分析は、変数間にリンクがあることを確認するための調査で使用されます。ただし、2つの変数間のリンクは、一方が他方を発生させることを意味しないため、相関関係は因果関係を意味しません。データポイントによく適合する基本的な線形回帰の線でさえ、状況と論理的な結果の間の関係を保証しない場合があります。線形回帰モデルを使用して、変数間に相関関係があるかどうかを判断できます。リンクの正確な性質と、一方の変数がもう一方の変数を引き起こすかどうかを判断するには、追加の調査と統計分析が必要になります。
線形回帰の基本的な仮定は何ですか？
線形回帰では、3つの重要な仮定があります。従属変数と独立変数は、何よりもまず、線形接続を持っている必要があります。この関係を確認するために、従属変数と独立変数の散布図が使用されます。次に、データセット内の独立変数間に多重共線性が最小またはゼロである必要があります。これは、独立変数が無関係であることを意味します。ドメイン要件によって決定される値を制限する必要があります。等分散性は3番目の要因です。エラーが均等に分散されるという仮定は、最も重要な仮定の1つです。