負の二項回帰入門:ステップバイステップガイド
公開: 2022-04-17負の二項回帰の手法は、カウント変数のモデリングを実行するために使用されます。 この方法は、重回帰法とほぼ同じです。 ただし、負の二項回帰の場合、従属変数、つまりYが負の二項分布に従うという違いがあります。 したがって、変数の値は、0、1、2などの非負の整数にすることができます。
この方法は、平均が分散に等しいと仮定して緩和するポアソン回帰の拡張でもあります。 「NB2」として定義される二項回帰の従来のモデルの1つは、ポアソンガンマの混合分布に基づいています。
ポアソン回帰の方法は、ガンマノイズの変数を追加することで一般化されます。 この変数の値は平均1であり、尺度パラメーターは「v」です。
負の二項回帰のいくつかの例を次に示します。
- 学校の管理者は、2つの学校の高校生の出席行動を調査するための調査を実施しました。 出席行動に影響を与える可能性のある要因には、後輩が学校を休んだ日が含まれる可能性があります。 また、彼らが登録されたプログラム。
- 健康関連の研究者が、過去12か月間に何人の高齢者が病院を訪れたかを調査しました。 この調査は、個人の特性と高齢者が購入した健康保険に基づいています。
負の二項回帰の例
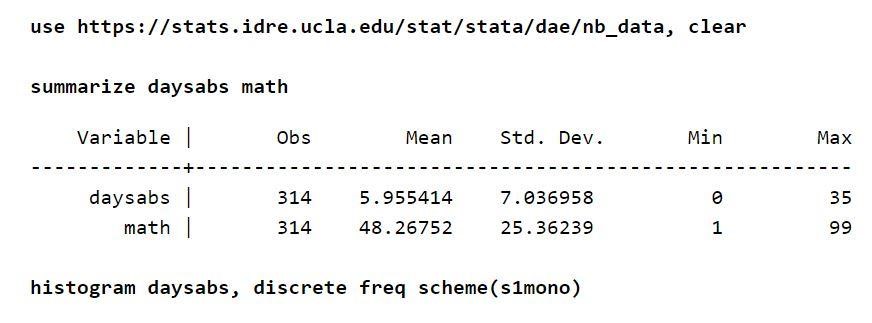
高校生約314人の出席シートがあるとします。 データは2つの都市の学校から取得され、nb_data.dtaという名前のファイルに保存されます。 この例で興味深い応答変数は、「daysabs」である不在日です。 すべての生徒の数学のスコアを定義する1つの変数「数学」が存在します。 「prog」という別の変数があります。 この変数は、学生が登録されているプログラムを示します。
ソース

各変数には、約314個の観測値があります。 したがって、変数間の分布も合理的です。 また、結果変数を考慮すると、無条件平均は分散よりも低くなります。
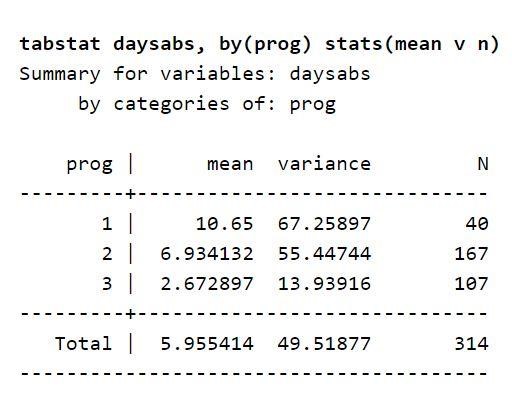
ここで、データセットで考慮されている変数の説明に注目してください。 表は、すべてのプログラムタイプで学生が学校を欠席した平均日数を表にしたものです。 これは、変数タイプのプログラムが、生徒が学校を休んだ日を予測できることを示唆しています。 また、結果変数を予測するために使用することもできます。 これは、結果変数の平均値が変数progによって異なるためです。 また、分散の値は、変数progの各レベルよりも高くなります。 これらの値は、分散および平均と呼ばれます。 既存の違いは、過剰分散の存在を示唆しているため、負の二項モデルを使用することが適切です。
ソース
研究者は、このタイプの研究のためにいくつかの分析方法を検討することができます。 これらの方法を以下に説明します。 ユーザーが回帰モデルの分析に使用できる分析方法のいくつかは次のとおりです。
1.負の二項回帰
負の二項回帰の方法は、データが過度に分散している場合に使用されます。 これは、条件付き分散の値が条件付き平均の値よりも高いか、それを超えていることを意味します。 この方法は、ポアソン回帰法から一般化されたものと見なされます。 これは、両方の方法が同じ平均構造を持っているためです。 ただし、過分散をモデル化するために使用される負の二項回帰には、追加のパラメーターがあります。 条件付き分布が結果変数から過度に分散している場合、信頼区間は情熱回帰よりも狭いと見なされます。
2.ポアソン回帰
ポアソン回帰の方法は、カウントデータのモデリングに使用されます。 ポアソン回帰のカウント変数をモデル化するために、多くの拡張機能を使用できます。
3.OLS回帰
カウント変数の結果は、対数変換されることがあり、OLS回帰の方法で分析されます。 ただし、OLS回帰の方法に関連する問題が発生する場合があります。 これらの問題は、値ゼロの対数を考慮して未定義の値が生成されることによるデータの損失である可能性があります。 また、分散データのモデリングが不足しているために生成される可能性があります。
4.ゼロ膨張モデル
これらのタイプのモデルは、モデル内のすべての過剰なゼロを考慮に入れようとします。
負の二項回帰を使用した分析
コマンド「nbreg」は、負の二項回帰のモデルを推定するために使用されます。 変数「prog」の前に「i」があります。 「i」の存在は、変数が型因子、つまりカテゴリ変数であることを示します。 これらは、モデルのインジケーター変数として含める必要があります。

- モデルの出力は、反復ログで始まります。 それは、ポアソンのモデルのフィッティングから始まり、ヌルモデル、そして負の二項のモデルが続きます。 このメソッドは最尤推定を使用し、最終ログの値が変更されるまで反復を続けます。 ログの尤度は、モデルの比較に使用されます。
- 次の情報はヘッダーファイルにあります。
- ヘッダーのすぐ下に負の二項回帰の係数の情報があります。 係数は、p値、zスコアなどのエラーとともにすべての変数に対して生成されます。 また、すべての係数に対して95%の信頼区間があります。 「数学」変数の係数は-0.006であり、統計的に有意であることを示しています。 この結果は、変数「math」で1単位が増加した場合、不在日数の予想ログ数が0.006の値だけ減少することを意味します。 また、インジケーター変数である2. progの値は、2つのグループ(グループ2と参照グループ)間のログのカウントで予想される差です。
- ログ転送された過分散のパラメーター推定が実行され、変換されていない値とともに表示されます。 ポアソンモデルでは、値はゼロです。
- 係数表の下に比率検定尤度情報があります。 このモデルは、コマンド「margins」を使用することでさらに理解できます。
Pythonで負の二項回帰分析を行うプロセス
回帰プロセスを実行するために必要なパッケージは、Pythonからインポートする必要があります。 これらのパッケージは以下のとおりです。
- statsmodels.apiをsmとしてインポートします
- matplotlib.pyplotをpltとしてインポートします
- numpyをnpとしてインポート
- patsyimportdmatricesから
- パンダをpdとしてインポートする
負の二項回帰に関する考慮事項
負の二項回帰分析の方法を適用する際に考慮すべきことがいくつかあります。 これらには以下が含まれます:

- 小さなサンプルが存在する場合は、負の二項回帰法はお勧めしません。
- 場合によっては、過剰分散の原因となる可能性のある過剰なゼロが存在します。 これらのゼロは、データ生成を追加するプロセスが原因で生成される可能性があります。 このような場合は、ゼロ膨張モデルの方法を使用することをお勧めします。
- データ生成のプロセスでゼロが考慮されない場合、そのような場合は、ゼロ切り捨てモデルの方法を使用することをお勧めします。
- 計数データに関連する暴露変数があります。 変数は、イベントが発生する可能性がある時間を示します。 この変数は、負の二項回帰のモデルに組み込む必要があります。 これは、exp()のオプションを介して行われます。
- 負の二項回帰分析のモデルでは、結果変数を負の値にすることはできません。 また、露出変数の値を0にすることはできません。
- コマンド「glm」は、負の二項回帰分析メソッドを実行するためにも使用できます。 これは、ログのリンクと二項式のファミリーを介して実行できます。
- 残差を取得するには、コマンド「glm」が必要です。 これは、負の二項回帰のモデルに他の仮定があるかどうかを確認するためのものです。
- 疑似決定係数にはさまざまな尺度が存在します。 ただし、すべてのメジャーは、OLSの回帰で決定係数によって提供される情報と同様の情報を提供します。
結論
この記事では、負の二項回帰のトピックについて説明しました。 これは重回帰の方法とほぼ同じであり、ポアソン分布の一般化された形式であることがわかりました。 この方法にはいくつかの用途があります。 この手法は、Pythonプログラミング言語またはRでも適用できます。
老化などの研究への応用を示すいくつかのケーススタディもあります。 また、カウントデータで使用できる回帰の古典的なモデルは、ポアソン回帰、負の二項回帰、および等比回帰です。 これらのメソッドは線形モデルのファミリーに属し、Rシステムなどのほぼすべての統計パッケージに含まれていました。
機械学習に優れ、データの分野を探求したい場合は、upGradが提供する機械学習とAIのエグゼクティブPGプログラムのコースを確認できます。 したがって、機械学習の専門家になることを夢見ている働く専門家であれば、専門家の下で訓練を受ける経験を積んでください。 詳細については、当社のWebサイトをご覧ください。 ご不明な点がございましたら、当社のチームが迅速にサポートいたします。