25 機械学習インタビューの質問と回答 – 線形回帰
公開: 2022-09-08面接で一般的に使用される機械学習アルゴリズムについてデータ サイエンス志望者をテストすることは、一般的な方法です。 これらの従来のアルゴリズムは、線形回帰、ロジスティック回帰、クラスタリング、決定木などです。データ サイエンティストは、これらのアルゴリズムに関する深い知識を持っていることが期待されます。
さまざまな組織の採用マネージャーとデータ サイエンティストに相談して、面接で彼らが尋ねる典型的な ML の質問について知りました。 彼らの広範なフィードバックに基づいて、意欲的なデータ サイエンティストの会話に役立つ一連の質問と回答が用意されました。 線形回帰のインタビューの質問は、機械学習のインタビューで最も一般的です。 これらのアルゴリズムに関する Q&A は、4 つの一連のブログ投稿で提供されます。
最高の機械学習コースとオンライン AI コース
| LJMU の機械学習と AI の理学修士号 | IIITB の機械学習と AI のエグゼクティブ ポスト大学院プログラム | |
| IIITB の機械学習と NLP の上級認定プログラム | IIITB の機械学習と深層学習の上級認定プログラム | メリーランド大学のデータサイエンスと機械学習のエグゼクティブポスト大学院プログラム |
| すべてのコースを調べるには、以下のページにアクセスしてください。 | ||
| 機械学習コース | ||
各ブログ投稿では、次のトピックを取り上げます。
- 線形回帰
- ロジスティック回帰
- クラスタリング
- すべてのアルゴリズムに関連する決定木と質問
線形回帰を始めましょう!
1. 線形回帰とは?
簡単に言えば、線形回帰は、与えられたデータに適合する最良の直線を見つける方法です。つまり、独立変数と従属変数の間の最良の線形関係を見つける方法です。
技術的に言えば、線形回帰は、独立変数と従属変数の間で、任意のデータに対して最適な線形適合関係を見つける機械学習アルゴリズムです。 これは、ほとんどの場合、残差平方和法によって行われます。
需要の高い機械学習スキル
| 人工知能コース | Tableau コース |
| NLPコース | 深層学習コース |

2. 線形回帰モデルの仮定を述べます。
線形回帰モデルには、主に次の 3 つの仮定があります。
- モデルの形式に関する仮定:
従属変数と独立変数の間に線形関係があると仮定されます。 これは「線形性の仮定」として知られています。 - 残差に関する仮定:
- 正規性の仮定: 誤差項 ε (i)は正規分布していると仮定されます。
- ゼロ平均仮定: 残差の平均値がゼロであると仮定されます。
- 一定の分散の仮定:残差項は同じ (ただし未知の) 分散 σ 2 を持つと仮定されます。この仮定は、均一性または等分散性の仮定としても知られています。
- 独立誤差の仮定: 残差項は互いに独立していると仮定されます。つまり、ペアごとの共分散はゼロです。
- 推定量に関する仮定:
- 独立変数はエラーなしで測定されます。
- 独立変数は互いに線形独立しています。つまり、データに多重共線性はありません。
説明:
- これは自明です。
- 残差が正規分布していない場合、ランダム性が失われます。これは、モデルがデータ内の関係を説明できないことを意味します。
また、残差の平均はゼロでなければなりません。
Y (i)i = β 0 + β 1 x (i) + ε (i)
これは仮定された線形モデルで、ε は残差項です。
E(Y) = E( β 0 + β 1 x (i) + ε (i) )
= E( β 0 + β 1 x (i) + ε (i) )
残差 E(ε (i) ) の期待値 (平均) がゼロの場合、ターゲット変数とモデルの期待値は同じになり、モデルのターゲットの 1 つになります。
残差 (誤差項とも呼ばれる) は独立している必要があります。 これは、残差と予測値の間、または残差自体の間に相関関係がないことを意味します。 何らかの相関関係が存在する場合、回帰モデルが識別できない関係があることを意味します。 - 独立変数が互いに線形独立でない場合、最小二乗解 (または正規方程式の解) の一意性が失われます。
世界のトップ大学が提供する人工知能コースにオンラインで参加してください。ML と AI の修士号、エグゼクティブ ポストグラデュエート プログラム、高度な認定プログラムに参加して、キャリアを加速させましょう。
3. 特徴量エンジニアリングとは? モデリングの過程でどのように適用しますか?
機能エンジニアリングは、生データを機能に変換して、潜在的な問題を予測モデルにより適切に表すプロセスです。
、目に見えないデータのモデル精度が向上します。
簡単に言えば、機能エンジニアリングとは、問題をより適切に理解し、モデル化するのに役立つ新しい機能の開発を意味します。 特徴量エンジニアリングには、ビジネス主導型とデータ主導型の 2 種類があります。 ビジネス主導の機能エンジニアリングは、ビジネスの観点から機能を含めることを中心に展開します。 ここでの仕事は、ビジネス変数を問題の特徴に変換することです。 データ駆動型の特徴量エンジニアリングの場合、追加する特徴量には重要な物理的解釈はありませんが、モデルがターゲット変数を予測するのに役立ちます。
参考:無料のnlpコース!
特徴量エンジニアリングを適用するには、データセットを十分に理解している必要があります。 これには、与えられたデータが何であるか、それが何を意味するか、生の特徴が何であるかなどを知ることが含まれます。また、どの要因がターゲット変数に影響を与えるか、変数の物理的解釈が何であるかなど、問題について非常に明確な考えを持っている必要があります。など
4. 正則化の用途は何ですか? L1 と L2 の正則化について説明します。
正則化は、モデルの過剰適合の問題に取り組むために使用される手法です。 非常に複雑なモデルがトレーニング データに実装されると、過剰適合します。 場合によっては、単純なモデルがデータを一般化できず、複雑なモデルが過剰適合することがあります。 この問題に対処するために、正則化が使用されます。
正則化とは、コスト関数に係数項 (ベータ) を追加して、項にペナルティが課せられ、大きさが小さくなるようにすることです。 これは基本的に、データの傾向を捉えるのに役立ち、同時にモデルが複雑になりすぎないようにすることで過剰適合を防ぎます。
- L1 または LASSO 正則化: ここでは、係数の絶対値がコスト関数に追加されます。 これは、次の式で確認できます。 強調表示された部分は、L1 または LASSO 正則化に対応します。 この正則化手法ではまばらな結果が得られるため、特徴選択にもつながります。
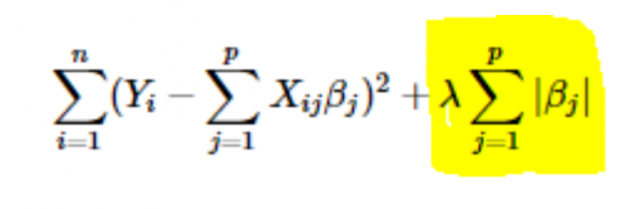
- L2 またはリッジ正則化: ここでは、係数の 2 乗がコスト関数に追加されます。 これは、次の式で見ることができます。ここで、強調表示された部分は、L2 またはリッジ正則化に対応しています。
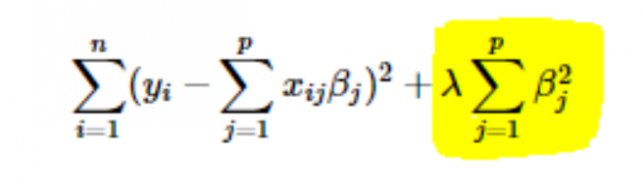
5. パラメータ学習率 (α) の値を選択する方法は?
学習率の値を選択するのは難しい作業です。 値が小さすぎると、勾配降下アルゴリズムが最適解に収束するまでに時間がかかります。 一方、学習率の値が高い場合、勾配降下法は最適解をオーバーシュートし、最適解に収束しない可能性が高くなります。
この問題を解決するには、値の範囲でさまざまなアルファ値を試し、コストと反復回数をプロットします。 次に、グラフに基づいて、急激な減少を示すグラフに対応する値を選択することができます。 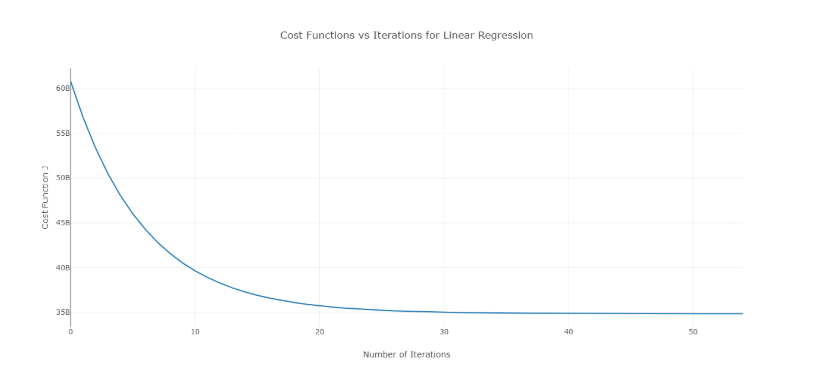
前述のグラフは、理想的なコスト対反復回数の曲線です。 コストは反復回数が増えるにつれて最初は減少しますが、特定の反復の後、勾配降下が収束し、コストはそれ以上減少しないことに注意してください。
反復回数に応じてコストが増加している場合は、学習率パラメーターが高く、減少させる必要があります。
6. 正則化パラメータ (λ) の値を選択する方法は?
正則化パラメーターの選択は難しい作業です。 λ の値が高すぎると、回帰係数 β の値が極端に小さくなり、モデルの適合不足 (高バイアス – 低分散) につながります。 一方、λ の値が 0 (非常に小さい) の場合、モデルはトレーニング データにオーバーフィットする傾向があります (低バイアス – 高分散)。
λ の値を選択する適切な方法はありません。 できることは、データのサブサンプルを用意して、異なるセットでアルゴリズムを複数回実行することです。 ここでは、人はどの程度の分散を許容できるかを決定する必要があります。 ユーザーが分散に満足したら、その値 λをデータセット全体に対して選択できます。
注意すべきことの 1 つは、ここで選択された λ の値が、トレーニング データ全体ではなく、そのサブセットに対して最適であったことです。
7. 時系列分析に線形回帰を使用できますか?
時系列分析に線形回帰を使用できますが、結果は有望ではありません。 そのため、通常、これを行うことはお勧めできません。 この背後にある理由は次のとおりです—
- 時系列データは主に将来の予測に使用されますが、線形回帰は外挿を目的としていないため、将来の予測に良い結果が得られることはめったにありません。
- ほとんどの場合、時系列データには、ピーク時や祝祭シーズンなどのパターンがあり、線形回帰分析で外れ値として扱われる可能性が最も高くなります。
8. 線形回帰の残差の合計はどの値に近いですか? 正当化します。
回答線形回帰の残差の合計は 0 です。線形回帰は、エラー (残差) が平均 0 で正規分布しているという仮定に基づいて機能します。つまり、
Y = β T X + ε
ここで、Y はターゲット変数または従属変数です。
βは回帰係数のベクトル、
X は、すべての機能を列として含む機能マトリックスです。
ε は、 ε ~ N(0,σ 2 ) となる残差項です。
したがって、すべての残差の合計は、残差の期待値にデータ ポイントの総数を掛けたものになります。 残差の期待値は 0 であるため、すべての残差項の合計はゼロです。
注: N(μ,σ 2 ) は、平均 μ と標準偏差 σ 2を持つ正規分布の標準表記です。
9.多重共線性は線形回帰にどのように影響しますか?
答え 多重共線性は、いくつかの独立変数が相互に (正または負の) 高度に相関している場合に発生します。 この多重共線性は、線形回帰の基本的な仮定に反するため、問題を引き起こします。 多重共線性の存在は、モデルの予測能力には影響しません。 したがって、予測だけが必要な場合、多重共線性の存在は出力に影響しません。 ただし、モデルから洞察を引き出して、たとえばビジネス モデルに適用しようとすると、問題が発生する可能性があります。
多重共線性によって引き起こされる主な問題の 1 つは、誤った解釈につながり、間違った洞察を提供することです。 線形回帰の係数は、フィーチャが 1 単位変化した場合のターゲット値の平均変化を示します。 したがって、多重共線性が存在する場合、1 つの特徴を変更すると相関変数が変化し、結果としてターゲット変数が変化するため、これは当てはまりません。 これは誤った洞察につながり、ビジネスに危険な結果をもたらす可能性があります。
多重共線性を処理する非常に効果的な方法は、VIF (Variance Inflation Factor) の使用です。 機能の VIF の値が高いほど、その機能はより直線的に相関します。 VIF 値が非常に高い機能を削除し、残りのデータセットでモデルを再トレーニングするだけです。
10. 線形回帰の正規形 (方程式) は? 勾配降下法より優先されるのはいつですか?
線形回帰の正規方程式は —
β=(X T X) -1 . X T Y
ここで、 Y=β T Xは線形回帰のモデルです。
Yはターゲット変数または従属変数です。
βは回帰係数のベクトルで、正規方程式を使用して到達します。
Xは、すべての機能を列として含む機能マトリックスです。
ここで、 X行列の最初の列はすべて 1 で構成されていることに注意してください。 これは、回帰直線のオフセット値を組み込むためです。
勾配降下法と正規方程式の比較:
| 勾配降下法 | 正規方程式 |
| アルファ(学習パラメータ)のハイパーパラメータ調整が必要 | そんな必要ない |
| これは反復プロセスです | 非反復プロセスです |
| O(kn 2 )時間計算量 | X T Xの評価によるO(n 3 ) 時間の計算量 |
| n が非常に大きい場合に優先 | n の値が大きいと非常に遅くなる |
ここで、' k ' は勾配降下法の最大反復回数であり、' n ' はトレーニング セット内のデータ ポイントの総数です。
明らかに、大規模なトレーニング データがある場合、正規方程式の使用は好まれません。 ' n ' の値が小さい場合、正規方程式は勾配降下法より高速です。
機械学習とは何か、なぜ重要なのか
11. データのさまざまなサブセットで回帰を実行すると、各サブセットで、特定の変数のベータ値が大幅に変化します。 ここで何が問題になる可能性がありますか?
このケースは、データセットが異種であることを意味します。 したがって、この問題を克服するには、データセットをさまざまなサブセットにクラスター化してから、クラスターごとに個別のモデルを構築する必要があります。 この問題に対処するもう 1 つの方法は、異種データを非常に効率的に処理できる決定木などのノンパラメトリック モデルを使用することです。

12. 線形回帰は実行されず、回帰係数の最良の推定値が無数にあることがわかります。 何が間違っている可能性がありますか?
この状態は、いくつかの変数間に完全な相関 (正または負) がある場合に発生します。 この場合、係数の一意の値は存在しないため、所定の条件が発生します。
13. 調整済み R 2とはどういう意味ですか? R 2とどう違うのですか?
調整済み R 2は、R 2と同様に、回帰直線の周囲にある点の数を表します。 つまり、モデルがトレーニング データにどれだけ適合しているかを示します。 調整済み R 2の式 は -
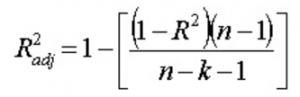
ここで、n はデータ ポイントの数、k は特徴の数です。
R 2の 1 つの欠点 新しい機能が役に立つかどうかに関係なく、新しい機能が追加されると常に増加するということです。 調整されたR 2 この欠点を克服します。 調整された R 2の値は、新しく追加された機能がモデルで重要な役割を果たす場合にのみ増加します。
14. 残差と適合値の曲線をどのように解釈しますか?
残差と適合値のプロットは、予測値と残差に相関関係があるかどうかを確認するために使用されます。 残差が正規分布しており、平均が適合値の周囲にあり、分散が一定である場合、モデルは正常に機能しています。 そうでない場合は、モデルに何らかの問題があります。
広範囲のデータセットでモデルをトレーニングするときに見られる最も一般的な問題は、不均一分散です(これについては、以下の回答で説明します)。 不均一分散の存在は、残差対適合値曲線をプロットすることで簡単に確認できます。
15. 異分散性とは何ですか? どのような結果になり、どうすればそれを克服できますか?
確率変数は、異なる部分母集団が異なる変動性 (標準偏差) を持つ場合、異分散であると言われます。
不均一分散の存在は、回帰分析で特定の問題を引き起こします。これは、誤差項が無相関であり、分散が一定であるという前提があるためです。 不均一分散の存在は、多くの場合、残差と適合値の円錐状の散布図の形で確認できます。
線形回帰の基本的な仮定の 1 つは、データに不均一分散が存在しないことです。 仮定に違反しているため、通常の最小二乗法 (OLS) 推定量は最良線形不偏推定量 (BLUE) ではありません。 したがって、他の線形不偏推定器 (LUE) よりも分散が最小になるわけではありません。
不均一分散を克服するための決まった手順はありません。 ただし、不均一分散の削減につながる可能性のある方法がいくつかあります。 彼らです -
- データの対数化: 指数関数的に増加している系列は、多くの場合、変動性が高くなります。 これは、対数変換を使用して克服できます。
- 加重線形回帰の使用: ここでは、OLS 法が X と Y の加重値に適用されます。1 つの方法は、従属変数の大きさに直接関連する重みを付加することです。
16. VIF とは何ですか? どのように計算しますか?
Variance Inflation Factor (VIF) は、データセット内の多重共線性の存在を確認するために使用されます。 次のように計算されます—
ここで、VIF jは j番目の変数の VIF の値です。
R j 2 その変数が他のすべての独立変数に対して回帰されたときのモデルの R 2値です。
変数の VIF の値が高い場合、R 2 対応するモデルの値が高い、つまり、他の独立変数がその変数を説明できる。 簡単に言えば、変数は他の変数に線形依存しています。
17. 線形回帰が特定のデータに適していることをどのように判断しますか?
線形回帰が特定のデータに適しているかどうかを確認するには、散布図を使用できます。 関係が線形に見える場合は、線形モデルを使用できます。 しかし、そうでない場合は、関係を線形にするためにいくつかの変換を適用する必要があります。 単純または単変量線形回帰の場合、散布図のプロットは簡単です。 ただし、多変量線形回帰の場合は、2 次元のペアワイズ散布図、回転プロット、動的グラフをプロットできます。
18.仮説検定は線形回帰でどのように使用されますか?
仮説検定は、次の目的で線形回帰で実行できます。
- 予測子がターゲット変数の予測にとって有意であるかどうかを確認します。 これには、次の 2 つの一般的な方法があります。
- p 値を使用すると、次のようになります。
変数の p 値が特定の制限 (通常は 0.05) より大きい場合、その変数はターゲット変数の予測において重要ではありません。 - 回帰係数の値を確認すると、次のようになります。
予測子に対応する回帰係数の値がゼロの場合、その変数はターゲット変数の予測において重要ではなく、ターゲット変数との線形関係はありません。
- p 値を使用すると、次のようになります。
- 計算された回帰係数が実際の係数の適切な推定値であるかどうかを確認します。
19. 線形回帰に関して勾配降下法を説明してください。
勾配降下法は最適化アルゴリズムです。 線形回帰では、コスト関数を最適化し、コスト関数の最適化された値に対応する β (推定量) の値を見つけるために使用されます。
勾配降下法は、ボールがグラフを転がり落ちるように機能します (慣性を無視します)。 ボールは最大勾配の方向に沿って移動し、平坦な表面 (最小) で停止します。 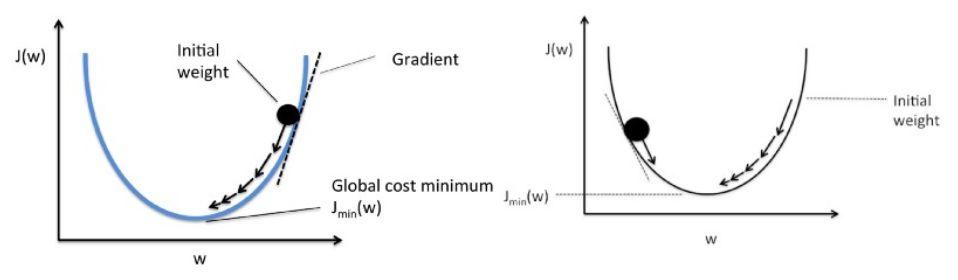
数学的には、線形回帰の勾配降下の目的は、次の解を見つけることです。
ArgMin J(Θ 0 ,Θ 1 )、ここで、J(Θ 0 ,Θ 1 ) は線形回帰のコスト関数です。 それは—によって与えられます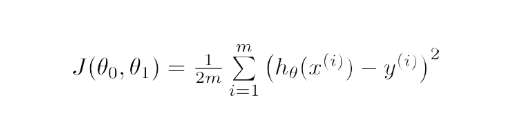
ここで、 hは線形仮説モデル、h=Θ 0 + Θ 1 x, yは真の出力で、 mはトレーニング セット内のデータ ポイントの数です。
勾配降下法は、ランダムな解から開始し、勾配の方向に基づいて、コスト関数がより低い値を持つ新しい値に解を更新します。
更新は次のとおりです。
収束するまで繰り返す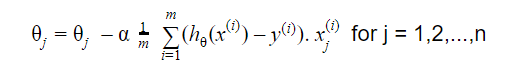
20. 線形回帰モデルをどのように解釈しますか?
線形回帰モデルは解釈が非常に簡単です。 モデルは次の形式です。 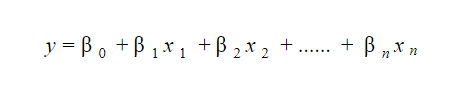
このモデルの重要性は、わずかな変化とその結果を簡単に解釈して理解できるという事実にあります。 たとえば、 x 0の値が1 単位増加し、他の変数が一定である場合、 yの値の総増加量はβ iになります。 数学的には、切片項 ( β 0 ) は、すべての予測子項がゼロに設定されているか、考慮されていない場合の応答です。
ヘルスケアを改善する 6 つの機械学習技術
21. ロバスト回帰とは?
回帰モデルは本質的に堅牢でなければなりません。 これは、いくつかの観測値が変更されても、モデルが大幅に変更されないことを意味します。 また、外れ値の影響をあまり受けないはずです。
OLS (通常の最小二乗法) を使用した回帰モデルは、外れ値に非常に敏感です。 この問題を克服するために、WLS (加重最小二乗法) 法を使用して回帰係数の推定量を決定できます。 ここでは、フィッティングの外れ値または高レバレッジ ポイントに与えられる重みが小さくなり、これらのポイントの影響が少なくなります。
22. モデルの当てはめの前に、どのグラフを観察することをお勧めしますか?
モデルをフィッティングする前に、変数の傾向、分布、歪度など、データを十分に認識しておく必要があります。 ヒストグラム、ボックス プロット、ドット プロットなどのグラフを使用して、変数の分布を観察できます。 これとは別に、従属変数と独立変数の間の関係を分析する必要もあります。 これは、散布図 (単変量の問題の場合)、回転プロット、動的プロットなどによって行うことができます。
23. 一般化線形モデルとは?
一般化線形モデルは、通常の線形回帰モデルの導関数です。 GLM は残差に関してより柔軟で、線形回帰が適切でないと思われる場合に使用できます。 GLM では、残差の分布を正規分布以外にすることができます。 リンク関数を使用して線形モデルをターゲット変数にリンクできるようにすることで、線形回帰を一般化します。 モデル推定は、最尤推定法を使用して行われます。
24. 偏りと分散のトレードオフを説明してください。
バイアスとは、モデルによって予測された値と実際の値との差を指します。 エラーです。 ML アルゴリズムの目標の 1 つは、バイアスを低くすることです。
分散とは、トレーニング データセットの小さな変動に対するモデルの感度を指します。 ML アルゴリズムのもう 1 つの目標は、分散を低くすることです。
正確に線形ではないデータセットの場合、バイアスと分散の両方を同時に低くすることはできません。 直線モデルは分散が小さいが偏りが大きく、次数の高い多項式は偏りが小さいが分散が大きい。
機械学習におけるバイアスと分散の関係から逃れることはできません。
- バイアスを減らすと、分散が増加します。
- 分散を小さくすると、バイアスが大きくなります。
したがって、この 2 つの間にはトレードオフがあります。 ML スペシャリストは、割り当てられた問題に基づいて、どの程度のバイアスと分散を許容できるかを決定する必要があります。 これに基づいて、最終的なモデルが構築されます。
25. 学習曲線は、より優れたモデルの作成にどのように役立ちますか?
学習曲線は、オーバーフィッティングまたはアンダーフィッティングの存在を示します。
学習曲線では、トレーニング エラーと交差検証エラーがトレーニング データ ポイントの数に対してプロットされます。 典型的な学習曲線は次のようになります。 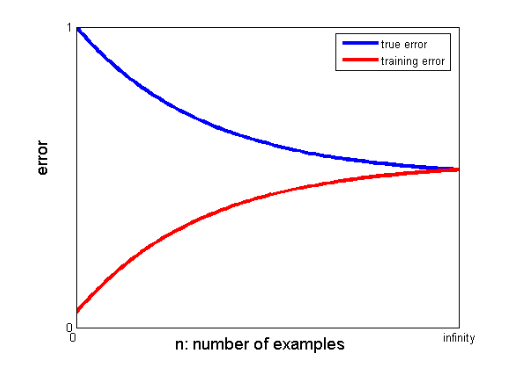
トレーニング エラーと真のエラー (交差検証エラー) が同じ値に収束し、対応するエラーの値が高い場合、モデルが適合不足であり、バイアスが高いことを示します。
機械学習のインタビューとそれらを達成する方法
機械学習面接は、種類やカテゴリによって異なります。たとえば、数人の採用担当者が線形回帰の面接で多くの質問をします。 機械学習エンジニアの面接を受けるときは、コーディング、研究、ケーススタディ、プロジェクト管理、プレゼンテーション、システム設計、統計などのカテゴリに特化できます。 最も一般的な種類のカテゴリと、それらに備える方法に焦点を当てます。
- コーディング
コーディングとプログラミングは、機械学習面接の重要な要素であり、応募者の選別によく使用されます。 これらの面接でうまくいくには、確かなプログラミング能力が必要です。 コーディング面接は通常 45 ~ 60 分で、2 つの質問のみで構成されます。 面接担当者はトピックを提示し、申請者ができるだけ短い時間でそれに取り組むことを期待します。
準備方法 – データ構造、時間と空間の複雑さ、管理スキル、および問題を理解して解決する能力を十分に理解することで、これらの面接に備えることができます。 upGradには優れたソフトウェア エンジニアリング コースが用意されており、コーディング スキルを向上させ、面接に合格するのに役立ちます。
2.機械学習
機械学習に対する理解度は、面接を通じて評価されます。 畳み込み層、再帰型ニューラル ネットワーク、生成的敵対ネットワーク、音声認識、およびその他のトピックは、雇用のニーズに応じてカバーされる場合があります。
準備方法 – この面接に合格するには、職務と責任を完全に理解している必要があります。 これは、学習する必要がある ML の仕様を特定するのに役立ちます。 ただし、仕様に出くわさない場合は、基本を深く理解する必要があります。 upGradが提供する ML の詳細なコースは、そのために役立ちます。 また、ML や AI に関する最新の記事を読んで最新のトレンドを理解し、定期的に取り入れることもできます。
3. スクリーニング
このインタビューはやや非公式であり、通常、インタビューの最初のポイントの 1 つです。 将来の雇用主がそれを処理することがよくあります。 この面接の主な目的は、応募者にビジネス、役割、義務の感覚を与えることです。 より非公式な雰囲気の中で、候補者は自分の過去についても質問され、関心のある分野が役職に一致するかどうかが判断されます。
準備方法 – これは面接の非常に非技術的な部分です。 これに必要なのは、あなたの正直さと、機械学習の専門分野の基本です。
4. システム設計
このようなインタビューでは、完全にスケーラブルなソリューションを最初から最後まで作成する能力をテストします。 大多数のエンジニアは、ある問題に夢中になりすぎて、全体像を見落としがちです。 システム設計の面接では、ソリューションを生み出すために組み合わせる多数の要素を理解する必要があります。 これらの要素には、フロントエンド レイアウト、ロード バランサー、キャッシュなどが含まれます。 これらの問題が十分に理解されていれば、効果的でスケーラブルなエンド ツー エンド システムの開発が容易になります。
準備方法 – システム設計プロジェクトの概念とコンポーネントを理解します。 プロジェクトの理解を深めるために、実際の例を使用して面接官に構造を説明します。
人気の機械学習と人工知能のブログ
| IoT: 歴史、現在、未来 | 機械学習のチュートリアル: ML を学ぶ | アルゴリズムとは? シンプル&イージー |
| インドのロボット工学エンジニアの給与:すべての役割 | 機械学習エンジニアの 1 日: 彼らは何をしているのか? | IoT(モノのインターネット)とは |
| 順列と組み合わせ:順列と組み合わせの違い | 人工知能と機械学習のトップ 7 トレンド | R による機械学習: 知っておくべきすべてのこと |

トレーニング エラーと交差検証エラーの収束値の間に有意なギャップがある場合、つまり、交差検証エラーがトレーニング エラーよりも大幅に大きい場合、モデルがトレーニング データを過適合しており、分散が大きいことを示唆しています。 .
機械学習エンジニア: 神話と現実
これで、このシリーズの最初のセクションは終了です。 ロジスティック回帰に基づく質問で構成されたシリーズの次の部分に固執してください。 お気軽にコメントを投稿してください。
共著 – Ojas Agarwal
機械学習と AI のエグゼクティブ PG プログラムを確認できます。このプログラムでは、実践的なハンズオン ワークショップ、1 対 1 の業界メンター、12 のケース スタディと課題、IIIT-B 卒業生ステータスなどを提供しています。
正則化で何がわかる?
正則化は、モデルの過剰適合の問題に対処するための戦略です。 複雑なモデルがトレーニング データに適用されると、オーバーフィッティングが発生します。 基本モデルではデータを一般化できない場合があり、複雑なモデルではデータが過剰適合する場合があります。 この問題を軽減するために正則化が使用されます。 正則化とは、最小化問題に係数項 (ベータ) を追加して、項がペナルティを受け、適度な大きさになるようにするプロセスです。 これは基本的に、モデルが複雑になりすぎるのを防ぐことでオーバーフィッティングを防ぎながら、データ パターンの識別に役立ちます。
特徴量エンジニアリングについて何を理解していますか?
元のデータを、潜在的な問題を予測モデルにより適切に説明する機能に変更し、目に見えないデータのモデル精度を向上させるプロセスは、機能エンジニアリングとして知られています。 簡単に言えば、機能エンジニアリングとは、問題の理解とモデリングを改善するのに役立つ追加機能の作成を指します。 機能エンジニアリングには、ビジネス主導型とデータ主導型の 2 種類があります。 商業的な観点からの機能の組み込みは、ビジネス主導の機能エンジニアリングの焦点です。
バイアスと分散のトレードオフとは何ですか?
モデルの予測値と実際の値とのギャップはバイアスと呼ばれます。 それは間違い。 低バイアスは、ML アルゴリズムの目的の 1 つです。 トレーニング データセットのわずかな変更に対するモデルの脆弱性は、分散と呼ばれます。 低分散は、ML アルゴリズムのもう 1 つの目標です。 完全に線形ではないデータセットで、偏りと分散の両方を低くすることは不可能です。 直線モデルの分散は小さいですがバイアスは大きく、高次多項式の分散は小さいですがバイアスは大きくなります。 機械学習では、偏りとばらつきの間のリンクは避けられません。
