Gaussian Naive Bayes:知っておくべきことは?
公開: 2021-02-22目次
ガウスナイーブベイズ
ナイーブベイズは、多くの分類関数に使用される確率的機械学習アルゴリズムであり、ベイズの定理に基づいています。 Gaussian Naive Bayesは、naiveBayesの拡張です。 他の関数を使用してデータ分布を推定しますが、トレーニングデータの平均と標準偏差を計算する必要があるため、ガウス分布または正規分布を実装するのが最も簡単です。
ナイーブベイズアルゴリズムとは何ですか?
Naive Bayesは、いくつかの分類タスクで使用できる確率的機械学習アルゴリズムです。 Naive Bayesの典型的なアプリケーションは、ドキュメントの分類、スパムのフィルタリング、予測などです。 このアルゴリズムは、トーマスベイズの発見に基づいているため、その名前が付けられています。
「ナイーブ」という名前が使用されているのは、アルゴリズムが互いに独立した機能をモデルに組み込んでいるためです。 1つの機能の値を変更しても、アルゴリズムの他の機能の値に直接影響することはありません。 Naive Bayesアルゴリズムの主な利点は、シンプルでありながら強力なアルゴリズムであるということです。
これは、アルゴリズムを簡単にコーディングできる確率モデルに基づいており、予測はリアルタイムで迅速に行われました。 したがって、このアルゴリズムは、ユーザーの要求に即座に応答するように調整できるため、実際の問題を解決するための一般的な選択肢です。 しかし、ナイーブベイズとガウスナイーブベイズを深く掘り下げる前に、条件付き確率が何を意味するのかを知る必要があります。
条件付き確率の説明
例を使用すると、条件付き確率をよりよく理解できます。 コインを投げると、先に進む確率や尻尾が出る確率は50%です。 同様に、面でサイコロを振ったときに4になる確率は、1/6または0.16です。
カードのパックを持っていくと、スペードであるという条件でクイーンを獲得する確率はどれくらいですか? スペードでなければならないという条件がすでに設定されているため、分母または選択セットは13になります。スペードにはクイーンが1つしかないため、スペードのクイーンを選ぶ確率は1/13=0.07になります。

イベントBが与えられた場合のイベントAの条件付き確率は、イベントBがすでに発生している場合にイベントAが発生する確率を意味します。 数学的には、Bが与えられた場合のAの条件付き確率は、P [A | B] = P [A AND B] /P[B]として表すことができます。
少し複雑な例を考えてみましょう。 合計100人の生徒がいる学校を受講してください。 この人口は、学生、教師、男性、女性の4つのカテゴリに分類できます。 以下の表を検討してください。
| 女性 | 男 | 合計 | |
| 先生 | 8 | 12 | 20 |
| 学生 | 32 | 48 | 80 |
| 合計 | 40 | 50 | 100 |
ここで、学校の特定の居住者が男性であるという条件を前提として、教師であるという条件付き確率はどのくらいですか。
これを計算するには、60人の男性のサブ母集団をフィルタリングし、12人の男性教師にドリルダウンする必要があります。
したがって、期待される条件付き確率P [Teacher | 男性]=12/60 = 0.2
P(教師|男性)= P(教師∩男性)/ P(男性)= 12/60 = 0.2
これは、Teacher(A)とMale(B)をMale(B)で割ったものとして表すことができます。 同様に、Aが与えられた場合のBの条件付き確率も計算できます。 ナイーブベイズに使用するルールは、次の表記法から結論付けることができます。
P(A | B)= P(A∩B)/ P(B)
P(B | A)= P(A∩B)/ P(A)
ベイズの定理
ベイズの定理では、トレーニングデータセットから見つけられるP(X | Y)からP(Y | X)を見つけます。 これを実現するには、上記の式でAとBをXとYに置き換えるだけです。 観測の場合、Xは既知の変数であり、Yは未知の変数です。 データセットの各行について、Xがすでに発生している場合、Yの確率を計算する必要があります。

しかし、Yに2つ以上のカテゴリがある場合はどうなりますか? 各Yクラスの確率を計算して、勝者を見つける必要があります。
ベイズの定理により、P(X | Y)からP(Y | X)を見つけます。
トレーニングデータからわかる:P(X | Y)= P(X∩Y)/ P(Y)
P(エビデンス|結果)
不明–テストデータで予測される:P(Y | X)= P(X∩Y)/ P(X)
P(結果|エビデンス)
ベイズの定理=P(Y | X)= P(X | Y)* P(Y)/ P(X)
ナイーブベイズ
ベイズの定理は、条件Xが与えられた場合のYの確率の式を提供します。しかし、現実の世界では、複数のX変数が存在する可能性があります。 独立した機能がある場合、ベイズルールをナイーブベイズルールに拡張できます。 Xは互いに独立しています。 ナイーブベイズの公式はベイズの公式よりも強力です
ガウスナイーブベイズ
これまでのところ、Xはカテゴリに含まれていますが、Xが連続変数である場合に確率を計算するにはどうすればよいですか? Xが特定の分布に従うと仮定すると、その分布の確率密度関数を使用して、尤度の確率を計算できます。
Xがガウス分布または正規分布に従うと仮定する場合、正規分布の確率密度を代入して、ガウスナイーブベイズと名付ける必要があります。 この式を計算するには、Xの平均と分散が必要です。
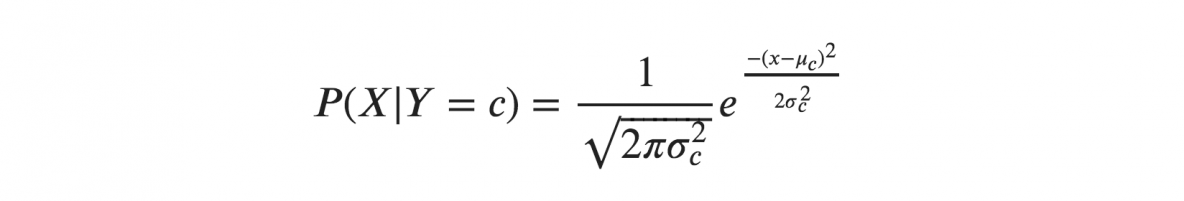
上記の式で、シグマとミューは、Yの特定のクラスcに対して計算された連続変数Xの分散と平均です。
ガウスナイーブベイズの表現
上記の式は、頻度を通じて各クラスの入力値の確率を計算しました。 分布全体の各クラスのxの平均と標準偏差を計算できます。
これは、各クラスの確率とともに、クラスのすべての入力変数の平均と標準偏差も保存する必要があることを意味します。
mean(x)= 1 / n * sum(x)
ここで、nはインスタンスの数を表し、xはデータの入力変数の値です。
標準偏差(x)= sqrt(1 / n * sum(xi-mean(x)^ 2))
ここで、各xの差の平均とxの平均の平方根が計算されます。ここで、nはインスタンスの数、sum()は合計関数、sqrt()は平方根関数、xiは特定のx値です。 。

ガウスナイーブベイズモデルによる予測
ガウス確率密度関数を使用して、パラメーターを変数の新しい入力値に置き換えることで予測を行うことができます。その結果、ガウス関数は新しい入力値の確率の推定値を提供します。
単純ベイズ分類器
単純ベイズ分類器は、1つの特徴の値が他の特徴の値から独立していることを前提としています。 単純ベイズ分類器は、分類に必要なパラメーターを推定するためのトレーニングデータを必要とします。 シンプルな設計とアプリケーションにより、単純ベイズ分類器は多くの実際のシナリオに適しています。
結論
Gaussian Naive Bayes分類器は、手間をかけずに高レベルの精度で非常にうまく機能する、迅速で単純な分類器手法です。
AI、機械学習について詳しく知りたい場合は、IIIT-BとupGradの機械学習とAIのPGディプロマをご覧ください。これは、働く専門家向けに設計されており、450時間以上の厳格なトレーニング、30以上のケーススタディと課題を提供します。 IIIT-B卒業生のステータス、5つ以上の実践的な実践的なキャップストーンプロジェクト、トップ企業との雇用支援。
世界のトップ大学からMLコースを学びましょう。 マスター、エグゼクティブPGP、または高度な証明書プログラムを取得して、キャリアを迅速に追跡します。
単純ベイズアルゴリズムとは何ですか?
ナイーブベイズは、古典的な機械学習アルゴリズムです。 統計に起源を持つナイーブベイズは、シンプルで強力なアルゴリズムです。 単純ベイズは、条件付き確率分析の適用に基づく分類器のファミリーです。 この分析では、イベントの条件付き確率は、イベントを構成する個々のイベントのそれぞれの確率を使用して計算されます。 単純ベイズ分類器は、特に機能セットの次元数が多い場合に、実際には非常に効果的であることがよくあります。
単純ベイズアルゴリズムのアプリケーションは何ですか?
Naive Bayesは、テキスト分類、ドキュメント分類、およびドキュメントのインデックス作成に使用されます。 単純ベイズでは、可能な各機能には前処理フェーズで割り当てられた重みがなく、後でトレーニングおよび認識フェーズで重みが割り当てられます。 単純ベイズアルゴリズムの基本的な仮定は、機能が独立しているということです。
Gaussian Naive Bayesアルゴリズムとは何ですか?
Gaussian Naive Bayesは、強力な独立性の仮定を持つベイズの定理の適用に基づく確率的分類アルゴリズムです。 分類の文脈では、独立性とは、ある特徴の値の存在が別の値の存在に影響を与えないという考えを指します(確率論の独立性とは異なります)。 ナイーブとは、オブジェクトの機能が互いに独立しているという仮定の使用を指します。 機械学習のコンテキストでは、単純ベイズ分類器は表現力が高く、スケーラブルで、適度に正確であることが知られていますが、トレーニングセットの成長に伴い、パフォーマンスは急速に低下します。 多くの機能が、単純ベイズ分類器の成功に貢献しています。 最も注目すべきは、分類モデルのパラメーターを調整する必要がなく、トレーニングデータセットのサイズに合わせて適切にスケーリングされ、連続的な特徴を簡単に処理できることです。
