知っておく必要のあるさまざまなタイプの回帰モデル
公開: 2022-01-07回帰問題は機械学習では一般的であり、それらを解決するための最も一般的な手法は回帰分析です。 これはデータモデリングに基づいており、ラインと各データポイントの間の距離が最小になるように、すべてのデータポイントを通過する最適なラインを作成する必要があります。 多くの異なる回帰分析手法が存在しますが、線形回帰とロジスティック回帰が最も顕著な手法です。 使用する回帰分析モデルのタイプは、最終的には関連するデータの性質によって異なります。
回帰分析とさまざまなタイプの回帰分析モデルについて詳しく見ていきましょう。
目次
回帰分析とは何ですか?
回帰分析は、データセット内の従属(ターゲット)変数と独立変数の間の関係を決定するための予測モデリング手法です。 これは通常、ターゲット変数に連続値が含まれ、従属変数と独立変数が線形または非線形の関係を共有する場合に使用されます。 したがって、回帰分析手法は、変数間の因果関係の決定、時系列モデリング、および予測に使用されます。 たとえば、企業の売上と広告費の関係は、回帰分析を使用して最もよく調べることができます。
回帰分析の種類
予測を行うために使用できる回帰分析手法には、さまざまな種類があります。 さらに、各手法の使用は、独立変数の数、回帰直線の形状、従属変数のタイプなどの要因によって決まります。
最も一般的に使用される回帰分析方法のいくつかを理解しましょう。
1.線形回帰
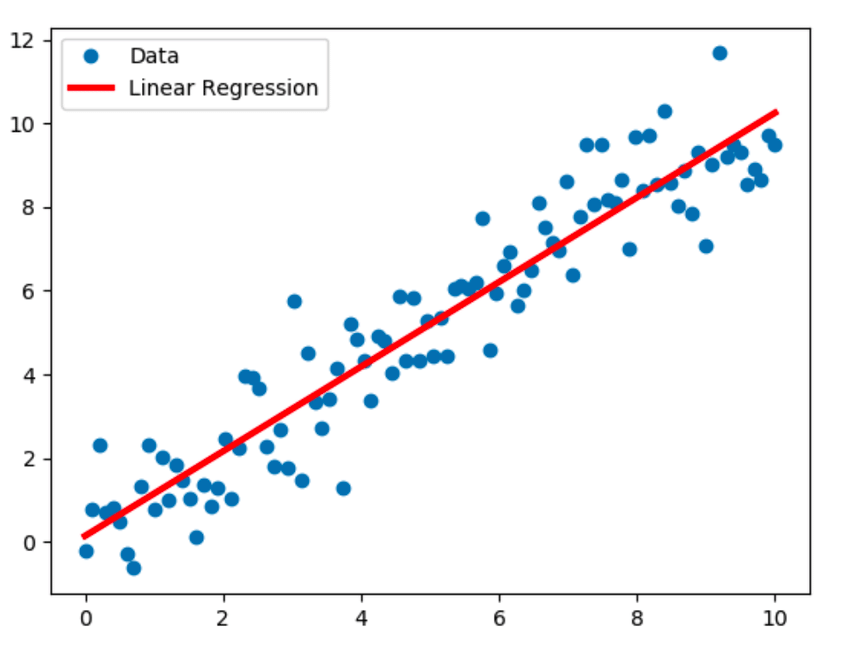
線形回帰は最も広く知られているモデリング手法であり、従属変数(Y)と独立変数(X)の間の線形関係を前提としています。 最適線とも呼ばれる回帰直線を使用して、この線形関係を確立します。 線形関係は、方程式Y = c + m * X + eで表されます。ここで、「c」は切片、「m」は直線の傾き、「e」は誤差項です。

線形回帰モデルは、単純(1つの従属変数と1つの独立変数)または複数(1つの従属変数と複数の独立変数)にすることができます。
ソース
2.ロジスティック回帰
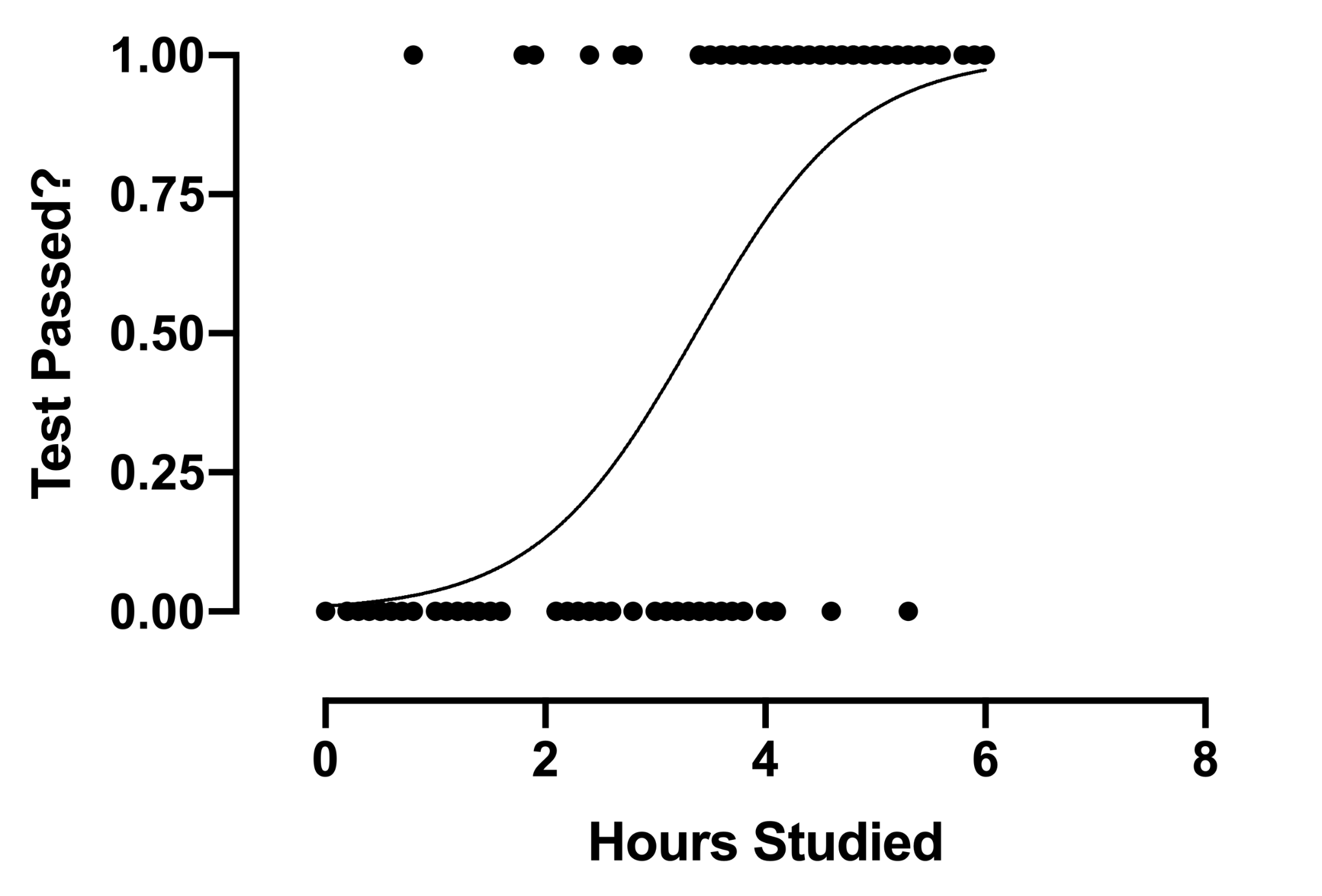
ロジスティック回帰分析手法は、従属変数が離散的である場合に使用されます。 つまり、この手法は、合格/不合格、真/偽、0/1などの相互に排他的なイベントの確率を推定するために使用されます。したがって、ターゲット変数は2つの値のうちの1つのみを持つことができ、シグモイド曲線は独立変数との関係。 確率の値の範囲は0から1です。
ソース
3.多項式回帰
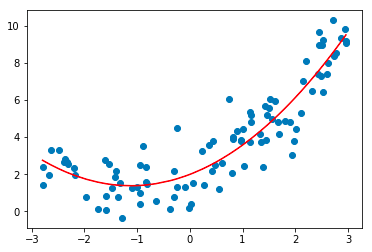
多項式回帰分析手法は、従属変数と独立変数の間の非線形関係をモデル化します。 これは多重線形回帰モデルの修正された形式ですが、すべてのデータポイントを通過する最適な線は曲線であり、直線ではありません。
ソース
4.リッジ回帰
データが多重共線性を示す場合、リッジ回帰分析手法が使用されます。 つまり、独立変数は高度に相関しています。 多重共線性の最小二乗推定は偏りがありませんが、それらの分散は、観測値を真の値から逸脱させるのに十分な大きさです。 リッジ回帰は、回帰推定にある程度のバイアスを導入することにより、標準誤差を最小限に抑えます。
リッジ回帰方程式のラムダ(λ)は、多重共線性の問題を解決します。
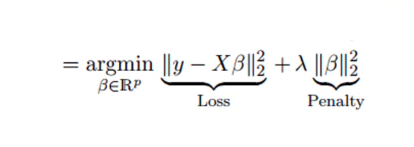
ソース
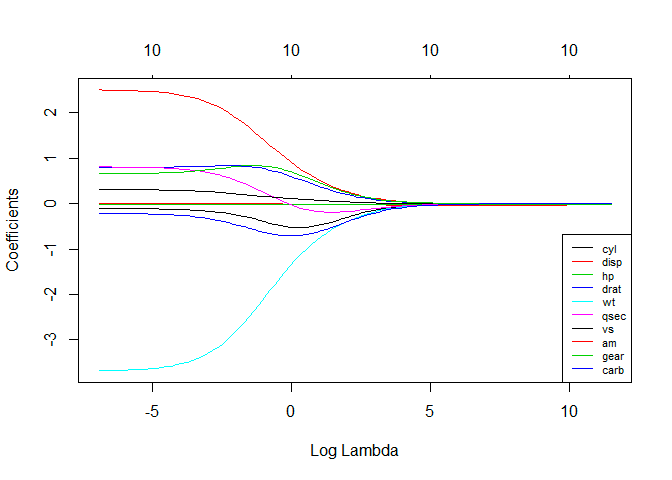
ソース
5.ラッソ回帰
リッジ回帰と同様に、ラッソ(Least Absolute Shrinkage and Selection Operator)回帰手法は、回帰係数の絶対サイズにペナルティを課します。 さらに、ラッソ回帰手法では変数選択が使用されるため、係数値は絶対零度に向かって縮小します。

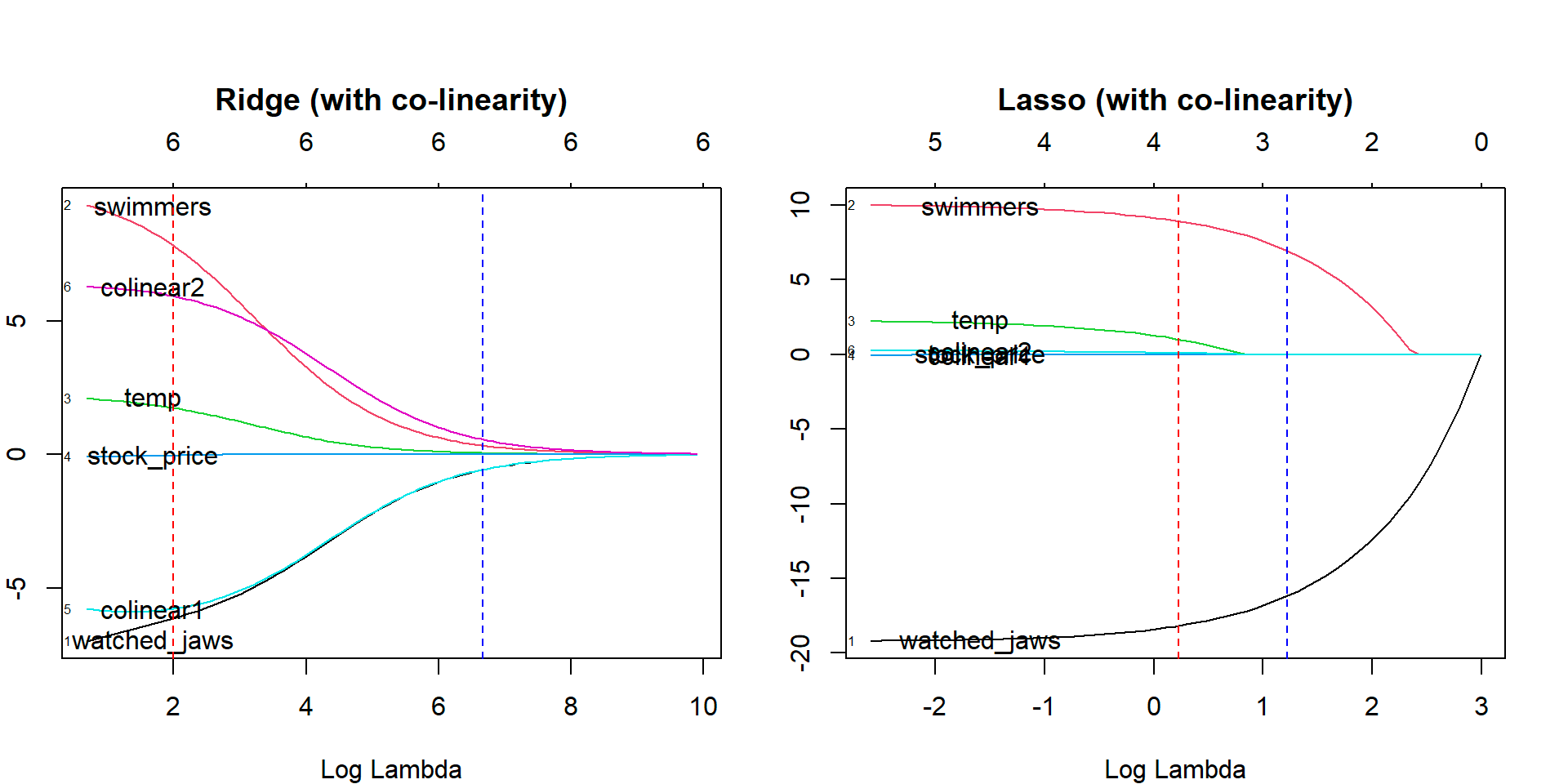
ソース
6.分位点回帰
分位点回帰分析手法は、線形回帰分析の拡張です。 線形回帰の条件が満たされていない場合、またはデータに外れ値がある場合に使用されます。 分位点回帰は、統計学と計量経済学のアプリケーションを見つけます。
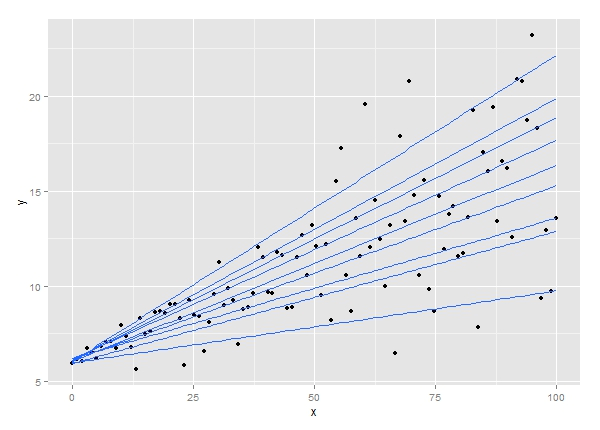
ソース
7.ベイズ線形回帰
ベイズ線形回帰は、ベイズの定理を利用して回帰係数の値を決定する、機械学習の回帰分析手法の1つです。 この手法では、最小二乗法を見つける代わりに、特徴の事後分布を決定します。 その結果、この手法は単純な線形回帰よりも安定性が高くなります。
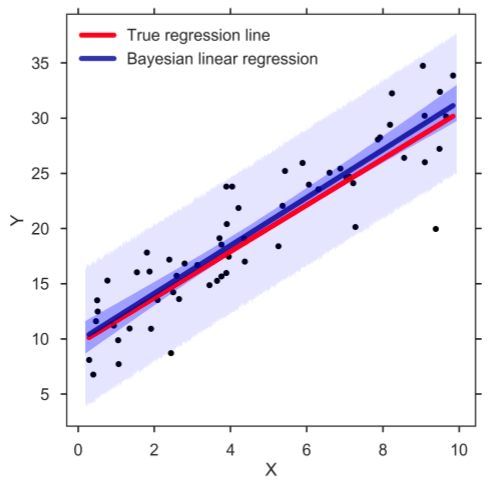
ソース
8.主成分回帰
主成分回帰手法は、通常、多重共線性を持つ重回帰データを分析するために使用されます。 リッジ回帰手法と同様に、主成分回帰法は、回帰推定にある程度のバイアスを与えることにより、標準誤差を最小限に抑えます。 この手法には2つのステップがあります。最初に主成分分析がトレーニングデータに適用され、次に変換されたサンプルがリグレッサーのトレーニングに使用されます。
9.部分最小二乗回帰
部分最小二乗回帰手法は、共分散に基づく迅速で効率的なタイプの回帰分析手法の1つです。 独立変数の数が多く、変数間の多重共線性が高い可能性がある回帰問題に役立ちます。 この手法は、変数をより小さな予測子のセットに減らし、回帰を実行するために使用されます。
10.エラスティックネット回帰
エラスティックネット回帰手法は、リッジ回帰モデルとラッソ回帰モデルのハイブリッドであり、相関性の高い変数を処理する場合に役立ちます。 リッジおよびラッソ回帰法のペナルティを使用して、回帰モデルを正則化します。
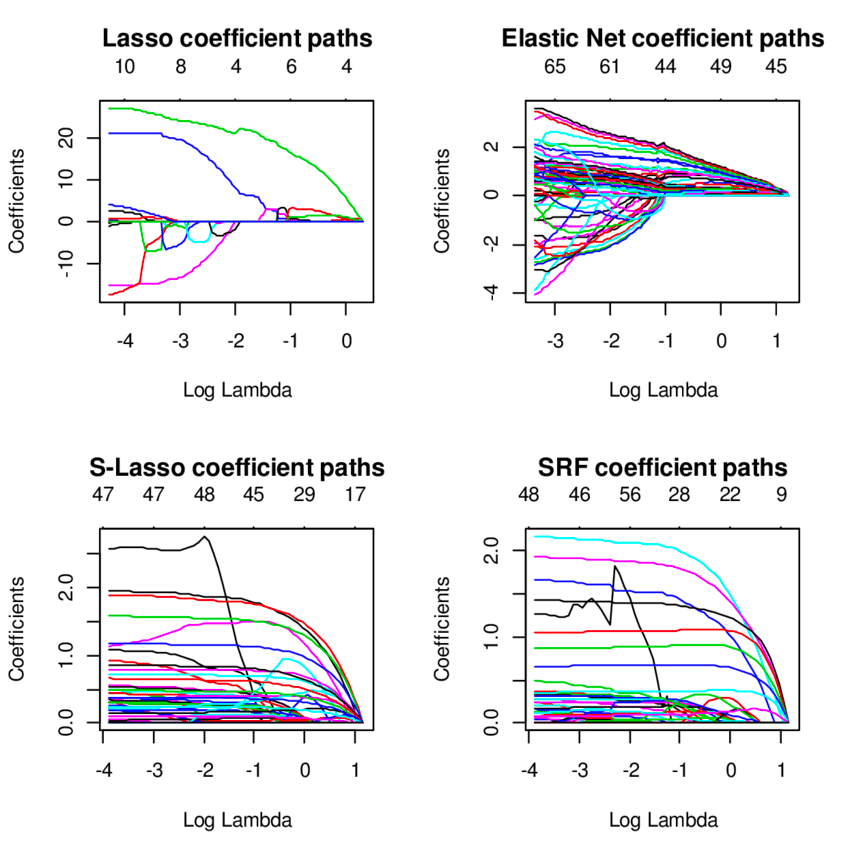
ソース
概要
ここで説明した回帰分析手法とは別に、機械学習では、生態学的回帰、ステップワイズ回帰、ジャックナイフ回帰、ロバスト回帰など、他のいくつかのタイプの回帰モデルが使用されます。 これらすべての異なるタイプの回帰手法の具体的な使用例は、利用可能なデータの性質と達成できる精度のレベルによって異なります。 全体として、回帰分析には2つの主要な利点があります。 これらは次のとおりです。

- 従属変数と独立変数の関係を示します。
- これは、従属変数に対する独立変数の影響の強さを示しています。
今後の方向性:機械学習とAIで理学修士号を取得する
機械学習と人工知能のキャリアに備えるための包括的なオンラインプログラムをお探しですか?
upGradは、リバプールジョンムーア大学とIIITバンガロアに関連して、機械学習とAIの修士号を提供し、多目的なAI専門家とデータサイエンティストを輩出しています。
包括的な20か月のオンラインプログラムは、ディープラーニング、NLP、グラフィカルモデル、強化学習などの高度な概念とスキルを習得したい専門家向けに特別に設計されています。 さらに、このプログラムは、Python、Keras、TensorFlow、Kubernetes、MySQLなどの主要なプログラミング言語やツールとともに統計の強固な基盤を提供することを目的としています。
プログラムのハイライト:
- リバプールジョンムーア大学で修士号を取得
- IIITバンガロアのエグゼクティブPGP
- 40以上のライブセッション、12以上のケーススタディとプロジェクト、11のコーディング割り当て、6つのキャップストーンプロジェクト
- 業界の専門家との25回以上のメンターシップセッション
- 360度のキャリア支援と学習支援
- ピアツーピアネットワーキングの機会
upGradは、世界クラスの教授陣、教育学、技術、業界の専門家を擁し、南アジア最大の高等教育工学プラットフォームとして浮上し、世界中の50万人以上の専門家に影響を与えました。 今日サインアップをしてください 80か国以上にまたがるupGradの40,000以上のグローバル学習者ベースの一部になるために!
1.回帰テストの定義とは何ですか?
回帰テストは、ソフトウェアのコード変更が既存の製品の機能に影響を与えていないかどうかを検証するために行われるソフトウェアテストの一種として定義されます。 これにより、製品が新しい機能や既存の機能への変更で適切に機能することが保証されます。 回帰テストには、既存の機能の動作条件をチェックするために再実行される、以前に実行されたテストケースの部分的または完全な選択が含まれます。
回帰モデルの目的は何ですか?
回帰分析は、独立変数に関する情報が利用できる場合に従属変数の値を予測するため、または従属変数に対する独立変数の影響を予測するための2つの目的のいずれかで行われます。
回帰分析は、独立変数に関する情報が利用できる場合に従属変数の値を予測するため、または従属変数に対する独立変数の影響を予測するための2つの目的のいずれかで行われます。
結果の正確性と妥当性を確保するには、適切なサンプルサイズが不可欠です。 回帰分析で適切なサンプルサイズを決定するための経験則はありませんが、変数ごとに少なくとも10個の観測値を考慮する研究者もいます。 したがって、3つの独立変数を使用する場合、最小サンプルサイズは30になります。多くの研究者は、統計式に従ってサンプルサイズを決定します。
