機械学習における連鎖律派生：説明

機械学習は、現在、そしてすべての正当な理由から、最も話題になり、研究されている分野の1つに進化しました。 機械学習の新しいモデルとアプリケーションが毎日発見されており、世界中の研究者が次の大きなことに取り組んでいます。

その結果、さまざまなバックグラウンドを持つ専門家が機械学習に切り替えて、この継続的な革命に参加することへの関心が高まっています。 あなたが最初の一歩を踏み出そうとしているそのような機械学習愛好家の一人なら、それは何よりもまず数学と統計の基礎を理解することから始まることを伝えましょう。

機械学習に非常に関連する数学のそのような重要なトピックの1つは、派生物です。 微積分の基本的な理解から、関数の導関数はその関数の瞬間的な変化率であることを覚えているでしょう。 このブログでは、デリバティブについてさらに深く掘り下げ、連鎖律を探ります。 方程式のいくつかの独立変数を変更すると、特定の関数の出力がどのように変化するかがわかります。 連鎖律の導関数の知識があれば、機械学習で必ず遭遇するより複雑な関数の差別化に取り組むことができます。

世界のトップ大学（修士、エグゼクティブ大学院プログラム、ML＆AIの高度な証明書プログラム）からオンラインで機械学習認定を取得して、キャリアを早急に進めましょう。

連鎖律派生物を理解する

連鎖律は本質的に、複合関数の導関数を計算するのに役立つ数式です。 複合関数は、2つ以上の関数で構成される関数です。 したがって、 fとgが2つの関数である場合、連鎖律は、 fogやgofなどの合成関数の導関数を見つけるのに役立ちます。

複合関数のフォグを考慮すると、連鎖律の導関数は次のようになります。

上記のルールは、次のように書くこともできます。

ここで、関数Fは、 f（g（x））の形式でのfとgの合成です。

ここで、3番目の変数（z）が2番目の変数（y）に依存し、2番目の変数（y）が最初の変数（x）に依存するような3つの変数があるとします。 その場合、連鎖律の導関数は次のようになります。

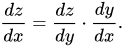ディープラーニングの観点から、これはバックプロパゲーションの問題を解決するために定期的に使用される式でもあります。 ここで、zはyに依存し、yはxに依存することを述べたので、z = f（y）およびy = g（x）と書くことができます。 この置換により、微分方程式が次のように変更されます。

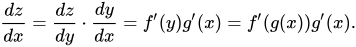それでは、その背後にある数学をよりよく理解するために、連鎖律の導関数のいくつかの例を見てみましょう。

連鎖律導関数の例と応用

ウィキペディアのよく知られた例を見て、連鎖律の導関数をよりよく理解しましょう。 空から自由落下していると仮定します。 秋に遭遇する大気圧は常に変化し続けます。 これは、この大気圧の変化を標高レベルとともにプロットしたグラフです。

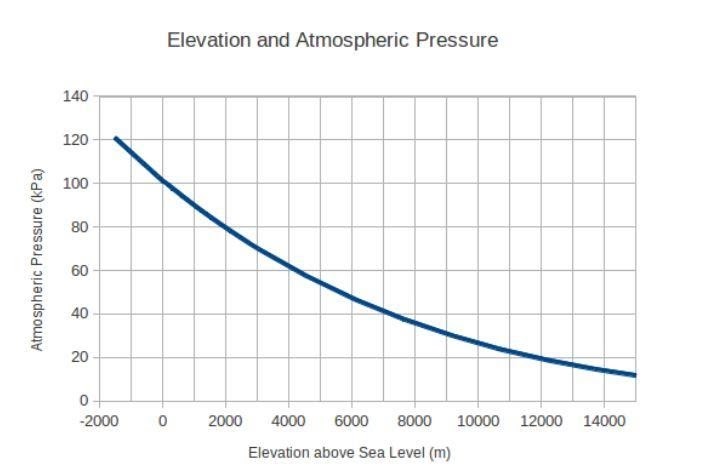
あなたの落下が海抜4000メートルで始まったとしましょう。 当初、速度はゼロで、重力のために加速度の値は毎秒9.8メートルの2乗でした。

それでは、この状況を以前の連鎖律法と比較してみましょう。 この例では、xの代わりに変数「t」を時間に使用します。

次に、変数y = g（t）は、落下の開始からの移動距離を示し、次のように与えられます。

g（t）= 0.5 * 9.8t ^ 2

また、海面からの高さは変数「h」で指定できます。これは400-g（t）に等しくなります。

モデルに基づいて、任意の高さhでの大気圧の関数を次のように書くこともできると仮定します。

f（h）= 101325 e−0.0001h

これで、従属変数に基づいて2つの方程式を区別して、次の結果を得ることができます。

g'（t）= −9.8t、

ここで、g'（t）は、任意の時間tにおける速度の値を示します。

f'（h）= −10.1325e−0.0001h

ここで、f'（h）は、高さhに対する大気圧の変化率です。 さて、問題は、これら2つの方程式を組み合わせて、時間に対する大気圧の変化率を導き出すことができるかということです。 連鎖律の使用を見てみましょう：

私たちが得た最後の方程式は、落下から経過した時間に対する大気圧の変化率を示しています。 機械学習の観点から、ニューラルネットワークは予測におけるニューロンのエラーに関する重みの更新を常に必要とします。 連鎖律は、これらの重みを調整し、機械学習モデルを正しい出力に近づけるのに役立ちます。

結論

ご覧のとおり、連鎖律は多くの目的に役立ちます。 特に機械学習や深層学習に関しては、連鎖律はニューロンの重みを更新し、モデルの全体的な効率を向上させるのに多くの用途があります。

連鎖律の基本を理解したので、先に進んで、自分でいくつかの問題を試してください。 いくつかの合成関数を調べて、それらの導関数を見つけてください。 練習すればするほど、概念が明確になり、機械学習モデルのトレーニングが容易になります。 とはいえ、機械学習の愛好家でありながら、この分野で最初の一歩を踏み出すのに苦労しているのであれば、upGradがあなたの背中になります！

機械学習とAIのエグゼクティブPGプログラムは、 IIITバンガロールと共同で提供され、業界に関連する6つの専門分野から選択できます。 コースは地上から始まり、業界の専門家による1対1のサポート、強力なピアグループの学生、および360度のキャリアサポートを提供しながら、頂点に到達します。