ベイズ統計とモデル：説明

ベイジアン手法は、データ分析とパラメーター推定で使用される統計のアプローチです。 このアプローチは、ベイズの定理に基づいています。

ベイズ統計は、統計モデルを使用して、観測されたパラメーターと観測されていないパラメーターの同時確率分布を決定するのに役立つ独自の原理に従います。 このシナリオで分析上の問題に取り組むには、統計の知識が不可欠です。

1770年代にトーマスベイズによってベイズの定理が導入されて以来、それは統計学において不可欠なツールであり続けています。 ベイジアンモデルは、統計学における最近の革新が、医学研究、Web検索の理解、自然言語の処理（自然言語処理）など、幅広い業界でマイルストーンを破るのに役立っているため、頻度主義モデルの古典的な代替品です。

たとえば、アルツハイマー病は、人が年をとるにつれて進行性のリスクをもたらすことが知られている病気です。 しかし、ベイズの定理の助けを借りて、医師は将来アルツハイマー病になる人の確率を推定することができます。 それはまた、人が彼の人生の後半に脆弱になる癌や他の加齢に関連した病気にも当てはまります。

頻繁な統計とベイズ統計

頻繁な統計とベイズ統計は一貫して、初心者にとって論争と悪夢のトピックであり、どちらも2つを選択するのは困難です。 20世紀初頭、ベイズ統計は不信と受容の問題を抱えていました。 しかし、時間の経過とともに、人々はベイズモデルの適用可能性とそれがもたらす正確な解に気づきました。

ここでは、頻繁な統計とそれに関連する複雑さを見ていきます。

頻繁な統計

これは、統計の世界で広く使用されている推論手法です。 イベント（仮説と呼ばれる）が発生したかどうかを分析します。 また、実験期間中に発生するイベントの確率も推定します。 望ましい結果が得られるまで、実験が繰り返されます。

それらの分布サンプルは実際のサイズであり、実験は理論的に無限に繰り返されます。 これは、コインの投げを研究するためにどのくらいの頻度の統計を使用できるかを示す例です。

• コインを1回投げる可能性は0.5（1/2）です。
• ヘッドの数は、実際に得られたリードの数を示します。
• トスの数が増えると、実際のヘッド数と予想されるヘッド数の差が大きくなります。

したがって、ここでは、結果は実験が繰り返される回数によって異なります。 これは頻繁な統計の大きな欠点です。

その設計と解釈の手法に関連する他の欠陥は、数値モデルへの頻繁な統計の適用がピークに達した20世紀に明らかになりました。

頻繁な統計の制限

頻繁な統計の3つの主要な欠陥を以下に示します。

1.変数p値

エンドポイントとサンプルサイズが変化すると、エンドポイントが定義された実験で固定サイズのサンプルに対して測定されたpの値が変化します。 これにより、1つのデータに対して2つのp値が得られますが、これは正しくありません。

2.一貫性のない信頼区間

CI（信頼区間）はサンプルサイズのみに依存します。 それは停止の可能性を無関係にします。

3.CIの推定値

信頼区間は確率分布ではなく、パラメーターの値は推定値であり、実際の値ではありません。

上記の3つの理由により、統計的問題に確率を適用するベイズアプローチが生まれました。

ベイズ統計の誕生

トーマスベイズ牧師は、1763年に書かれたエッセイで、統計に対するベイズアプローチを最初に提案しました。このアプローチは、過去に基づいて将来のイベントを予測する逆確率の戦略として、リチャードプライスによって公開されました。

このアプローチは、以下で説明するベイズの定理に基づいています。

ベイズの定理

レニーの確率の公理は、条件付き確率を調べます。ここで、イベントAとイベントBが発生する可能性は、依存または条件付きです。 基本的な条件付き確率は、次のように記述できます。

イベントBが発生する確率は、イベントAによって異なります。

上記の方程式は、ベイズの定理の数式であるベイズの定理の基礎です。

ここで、∩は交差点を示します。

ベイズの定理は次のように書くことができます。

ベイズルールはベイズ統計の基礎であり、統計モデルの特定のパラメーターに関する利用可能な情報が、収集されたデータと比較および更新されます。

背景知識は事前分布として表され、事後分布を見つけるための尤度関数として、観測または収集されたデータと比較および調査されます。

この事後分布は、将来のイベントに関する予測を行うために使用されます。

ベイジアンアプローチのアプリケーションは、次のパラメータに依存します。

1. 事前モデルとデータモデルの定義
2. 関連する推論を行う
3. モデルの精査と合理化

ベイジアンニューラルネットワークとは何ですか？

ベイジアンニューラルネットワーク（BNN）は、統計的方法論を使用して標準ネットワークを拡張し、事後推論を変更して過剰適合を追跡するときに作成するネットワークです。 これはベイジアンアプローチであるため、ニューラルネットワークのパラメーターに関連付けられた確率分布があります。

これらは、利用可能なデータの自由な流れがない複雑な問題を解決するために使用されます。 ベイジアンニューラルネットワークは、分子生物学や医療診断などの領域での過剰適合を制御するのに役立ちます。

ベイジアンニューラルネットワークを使用した1つの可能性だけでなく、質問に対する回答の全体的な分布を検討することができます。 これらは、モデルの選択/比較を決定し、正則化を伴う問題に対処するのに役立ちます。

ベイズ統計は、新しいデータまたは科学的証拠に関する主観的な知識を合理化および更新するための数学的ツールを提供します。 頻繁な統計的アプローチとは異なり、確率は同じ条件下で繰り返されるイベントの頻度に依存するという仮定に基づいて機能します。

要するに、ベイジアン手法は個人の仮定と意見の延長です。 より効率的にするベイズモデルの重要な側面は、受け取る情報の種類に基づいて個人の意見が異なることを理解していることです。

ただし、新しい証拠とデータが出現すると、個人には収束点、ベイズ推定があります。 この合理的な更新は、ベイズ統計の特別な機能であり、分析上の問題に対してより効果的になります。

ここで、確率0は、イベントが発生する見込みがない場合に適用され、確率1は、イベントが発生することが確実な場合に適用されます。 0と1の間の確率は、他の潜在的な結果の余地を与えます。

モデルからより良い推論を得るためにベイズ推定を達成するためにベイズルールが適用されるようになりました。

ベイズ推定を取得するためにベイズルールをどのように適用しますか？

次の方程式を考えてみましょう。

P（θ| D）= P（D |θ。）P（θ）/ P（D）

P（θ）は事前分布を示し、

P（θ| D）は事後信念を示し、

P（D）は証拠を表し、

P（D |θ）は可能性を示します。

ベイズ推定の主な目的は、信念と証拠をブレンドして更新された事後信念を取得するための合理的で数学的に正確な方法を提供することです。 事後の信念は、新しいデータが生成されるときに事前の信念として使用できます。 したがって、ベイズ推定は、ベイズの定理の助けを借りて、信念を継続的に更新するのに役立ちます。

同じコイントスの例を考えると、ベイジアンモデルは、新しいコイントスで前から後の信念に手順を更新します。 ベイズ法では、次の確率が得られます。

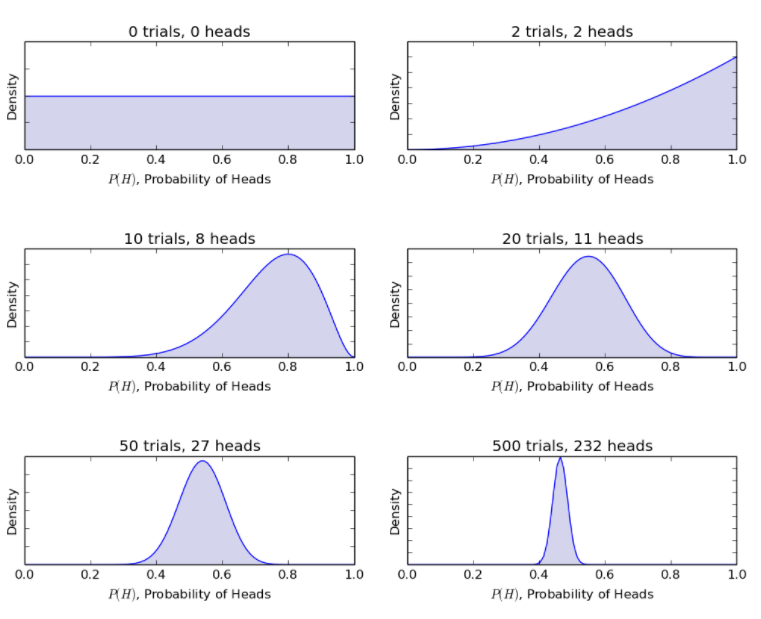
ソース

したがって、ベイジアンモデルでは、情報が制限されている不確実なシナリオを、かなりの量のデータを含むより定義されたシナリオに合理化できます。

ベイジアンモデルと頻度主義モデルの顕著な違い

頻繁な統計

ベイズ統計

目標は点推定と見なされ、CI

目標は事後分布と見なされます

手順は観察から始まります

プロセスは事前配布から始まります

新しい観測が行われるたびに、頻度主義的アプローチは既存のモデルを再計算します。

新しい観測が行われるたびに、事後分布（イデオロギー/仮説）が更新されます

例：平均、t検定、およびANOVAの推定。

例：高密度間隔の平均とオーバーラップの事後分布の推定。

ベイズ統計の利点

• それは、先入観のある情報を科学的証拠を備えた堅固な枠組みと融合させるための有機的で単純な手段を提供します。 パラメータに関する過去の情報は、将来の調査のための事前分布を形成するために使用できます。 推論はベイズの定理に準拠しています。
• ベイズモデルからの推論は論理的かつ数学的に正確であり、大雑把な仮定ではありません。 サンプルのサイズに関係なく、精度は一定に保たれます。
• ベイズ統計は、尤度原理に従います。 2つの異なるサンプルが信念θに対して共通の尤度関数を持っている場合、信念に関するすべての推論は類似している必要があります。 従来の統計手法は、強い尤度原理に従いません。
• ベイズ分析からの解は簡単に解釈できます。
• 階層モデルや不完全なデータの問題など、さまざまなモデルに役立つプラットフォームを提供します。 すべてのパラメトリックモデルの計算は、他の数値手法を使用して仮想的に追跡できます。

歴史を超えたベイズモデルの成功したアプリケーション

ベイジアン法は、第二次世界大戦中に多くの成功したアプリケーションを持っていました。 それらのいくつかを以下に示します。

• ロシアの統計家であるアンドレイ・コルモゴロフは、ベイズ法を使用してロシアの大砲の効率を改善することに成功しました。
• ベイジアンモデルは、ドイツのUボートのコードを破るために使用されました。
• フランス生まれのアメリカ人数学者、バーナード・コープマンは、無線送信を傍受するベイズモデルの助けを借りて、同盟国がドイツのUボートの位置を特定するのを助けました。

ベイズ統計について詳しく知りたい場合は、upGradの機械学習とクラウドの高度な認定を取得して、実際の業界プロジェクトとケーススタディを通じて基礎となる概念を理解してください。 12か月のコースは、IITマドラスによって提供され、自習型学習をサポートします。

詳細については、お問い合わせください。