Was ist Bayes'sches Denken? Einführung und Theorem

Ein statistisches Theorem des englischen Statistikers und Philosophen Thomas Bayes aus dem 17. Jahrhundert ist nach wie vor ein Leitfaden für Wissenschaftler und Analysten auf der ganzen Welt. Heutzutage findet Bayes'sches Denken Anwendung in Medizin, Wissenschaft, Technologie und mehreren anderen Disziplinen und beeinflusst unser Weltbild und die daraus resultierenden Handlungen weiterhin stark.

Die Bayes-Idee von Thomas war verblüffend einfach. Laut Bayes hängt die Wahrscheinlichkeit, dass eine Hypothese wahr ist, von zwei Bedingungen ab: wie vernünftig sie auf dem basiert, was wir bereits wissen (das Vorwissen) und wie gut sie zu neuen Beweisen passt. Somit unterscheidet sich Bayes'sches Denken von traditionellen Hypothesentests dadurch, dass Ersteres das Vorwissen einbezieht, bevor vorschnelle Schlussfolgerungen gezogen werden.

Lassen Sie uns mit Blick auf die vorläufige Einführung etwas detaillierter auf die Bayes'sche Statistik eingehen.

Bayessche Statistik

Einfach ausgedrückt wendet die Bayes'sche Statistik Wahrscheinlichkeiten auf statistische Probleme an, um frühere Überzeugungen im Lichte neuer Daten zu aktualisieren. Die Wahrscheinlichkeit drückt einen Grad des Glaubens an ein bestimmtes Ereignis aus.

Der Grad der Überzeugung kann auf vorherigem Wissen über das Ereignis basierend auf persönlichen Annahmen oder Ergebnissen früherer Experimente beruhen. Die Bayes'sche Statistik verwendet das Theorem von Bayes, um Wahrscheinlichkeiten zu berechnen. Das Theorem von Bayes wiederum beschreibt die bedingte Wahrscheinlichkeit eines Ereignisses basierend auf neuen Beweisen und früheren Informationen, die sich auf das Ereignis beziehen.

Lassen Sie uns vor diesem Hintergrund das grundlegende Konzept der bedingten Wahrscheinlichkeit auffrischen, bevor wir den Satz von Bayes im Detail verstehen.

Bedingte Wahrscheinlichkeit

Die bedingte Wahrscheinlichkeit kann als die Wahrscheinlichkeit eines Ereignisses oder Ergebnisses basierend auf dem Eintreten eines früheren Ereignisses oder Ergebnisses definiert werden. Sie wird berechnet, indem die Wahrscheinlichkeit des vorherigen Ereignisses mit der Wahrscheinlichkeit des nachfolgenden oder bedingten Ereignisses multipliziert wird.

Schauen wir uns ein Beispiel an, um das Konzept besser zu verstehen .

• Ereignis A ist, dass eine Familie, die einen Ausflug plant, ein Picknick macht. Es besteht eine Wahrscheinlichkeit von 80 %, dass die Familie zum Picknick geht.
• Ereignis B ist, dass es an dem Tag regnen wird, an dem die Familie ein Picknick macht. Laut Wettervorhersage besteht am Picknicktag eine Niederschlagswahrscheinlichkeit von 60 %.
• Daher wird die Wahrscheinlichkeit (P), dass die Familie zum Picknick geht und es regnet, wie folgt berechnet:

P (Picknick und Regen) = P (Regen | Picknick) P (Picknick) = (0,60) * (0,80) = 0,48

Im obigen Beispiel betrachtet die bedingte Wahrscheinlichkeit die beiden Ereignisse A und B in Beziehung zueinander, also die Wahrscheinlichkeit, dass die Familie zum Picknick geht und es am selben Tag auch regnet.

Daher unterscheidet sich die bedingte Wahrscheinlichkeit von der unbedingten Wahrscheinlichkeit, da sich letztere auf die Wahrscheinlichkeit des Eintretens eines Ereignisses bezieht, unabhängig davon, ob ein anderes Ereignis oder andere Ereignisse stattgefunden haben oder andere Bedingungen vorliegen.

Die Formel für die bedingte Wahrscheinlichkeit

Die Formel für die bedingte Wahrscheinlichkeit stammt aus der Wahrscheinlichkeitsmultiplikationsregel:

P (A und B) oder P (AUB) = P ( B gegeben A) oder P (B | A) * P (A)

In der obigen Gleichung ist P (A und B) die gemeinsame Wahrscheinlichkeit, die sich auf die Wahrscheinlichkeit bezieht, dass zwei oder mehr Ereignisse gleichzeitig auftreten. Es wird auch als P (A,B) geschrieben.

So leiten Sie die bedingte Wahrscheinlichkeitsgleichung aus der Multiplikationsregel ab:

Schritt 1: Schreiben Sie die Multiplikationsregel auf.

P (A und B) = P (B | A) * P (A)

Schritt 2: Teilen Sie beide Seiten der Gleichung durch P (A).

P (A und B) / P (A) = P (B | A) * P (A) / P (A)

Schritt 3: Streiche P (A) auf der rechten Seite der Gleichung.

P (A und B) / P (A) = P (B | A)

Schritt 4: Schreiben Sie die Gleichung um.

P (A und B) = P (B | A) / P (A)

Somit lautet die Formel für die bedingte Wahrscheinlichkeit:

P (A und B) = P (B | A) / P (A)

Satz von Bayes

Mit dem Satz von Bayes können wir unsere Überzeugungen und Überzeugungen auf der Grundlage neuer und relevanter Beweise aktualisieren. Wenn wir zum Beispiel versuchen herauszufinden, mit welcher Wahrscheinlichkeit eine bestimmte Person an Krebs erkrankt ist, würden wir im Allgemeinen davon ausgehen, dass es sich um den Prozentsatz der Bevölkerung handelt, der an Krebs erkrankt ist. Wenn wir jedoch zusätzliche Beweise einführen, z. B. dass die betreffende Person regelmäßig raucht, können wir unsere Wahrnehmung (und damit die Wahrscheinlichkeit) aktualisieren, da die Wahrscheinlichkeit, an Krebs zu erkranken, höher ist, wenn eine Person Raucher ist. Daher nutzen wir sowohl unser Vorwissen als auch die zusätzlichen Beweise, um unsere Schätzungen zu verbessern.

Die Formel für den Satz von Bayes

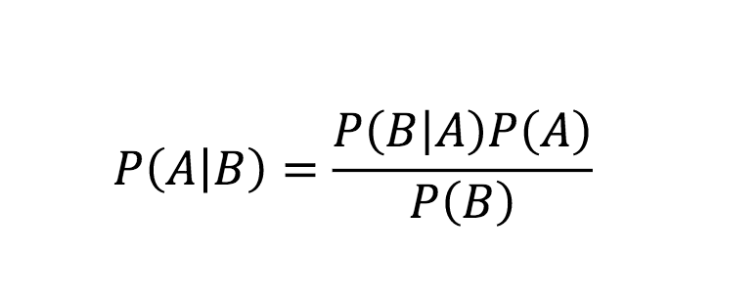
Quelle

Die obige Gleichung ist die Regel von Bayes. Betrachten wir nun die schrittweise Ableitung der Gleichung des Satzes von Bayes.

Schritt 1: Betrachten Sie zwei Ereignisse, A und B. A ist das Ereignis, dessen Wahrscheinlichkeit wir berechnen möchten, und B ist der zusätzliche Beweis, der sich auf A bezieht.

Schritt 2: Schreiben Sie die Beziehung zwischen der gemeinsamen Wahrscheinlichkeit und der bedingten Wahrscheinlichkeit der Ereignisse A und B auf.

P (A,B) = P (A | B) * P(B) = P (B,A) = P (B | A) * P(A)

Schritt 3: Setze die beiden bedingten Wahrscheinlichkeitsterme gleich.

P (A | B) * P (B) = P (B | A) * P (A)

Schritt 4: Teilen Sie beide Seiten der Gleichung durch P (B).

P (A | B) * P (B) / P (B) = P (B | A) * P (A) / P (B)

Schritt 5: Streiche P (B) auf der linken Seite der Gleichung.

P (A | B) = P (B | A) * P (A) / P (B)

Somit erhalten wir die Formel des Satzes von Bayes wie folgt:

P (A | B) = P (B | A) * P (A) / P (B)

Verstehen der Terme in der Gleichung des Satzes von Bayes

P (A | B) = P (B | A) * P (A) / P (B)

• P (A | B) wird die spätere Wahrscheinlichkeit oder die Wahrscheinlichkeit genannt, die wir zu schätzen versuchen. Basierend auf dem vorherigen Beispiel wäre die A-posteriori-Wahrscheinlichkeit die Wahrscheinlichkeit, dass die Person Krebs hat, vorausgesetzt, dass die Person ein regelmäßiger Raucher ist.
• P (B | A) wird die Wahrscheinlichkeit genannt und bezieht sich auf die Wahrscheinlichkeit, die zusätzlichen Beweise zu entdecken, wenn unsere Ausgangshypothese gegeben ist. Im obigen Beispiel ist die Wahrscheinlichkeit die Wahrscheinlichkeit, dass die Person Raucher ist, vorausgesetzt, dass die Person Krebs hat.
• P (A) ist die vorherige Wahrscheinlichkeit oder die Wahrscheinlichkeit unserer Hypothese ohne zusätzliche Beweise oder Informationen. Im obigen Beispiel ist die vorherige Wahrscheinlichkeit die Wahrscheinlichkeit, Krebs zu haben.
• P (B) ist die marginale Wahrscheinlichkeit oder die Gesamtwahrscheinlichkeit, die Beweise zu beobachten. Im Kontext des obigen Beispiels ist die marginale Wahrscheinlichkeit die Wahrscheinlichkeit, Raucher zu sein.

Ein einfaches Beispiel zum Verständnis des Satzes von Bayes

Anhand einiger hypothetischer Zahlen im vorherigen Beispiel werden wir die Auswirkungen der Anwendung des Satzes von Bayes sehen.

Angenommen, die Wahrscheinlichkeit, an Krebs zu erkranken, beträgt 0,06, das heißt, 6 % der Menschen haben Krebs. Nehmen wir nun an, dass die Wahrscheinlichkeit, Raucher zu sein, 0,20 beträgt, oder 20 % der Menschen sind Raucher, und 30 % der Menschen mit Krebs sind Raucher. Also, P (Raucher | Krebs) = 0,30.

Anfangs beträgt die Wahrscheinlichkeit, an Krebs zu erkranken, lediglich 0,06 (vorher). Aber mit den neuen Erkenntnissen können wir P (Krebs | Raucher) = P ((Raucher | Krebs) * P (Krebs)) / P (Raucher) = (0,30*0,06) / (0,20) = 0,09 berechnen.

Lernen Sie Data Science-Kurse online von den besten Universitäten der Welt. Verdienen Sie Executive PG-Programme, Advanced Certificate-Programme oder Master-Programme, um Ihre Karriere zu beschleunigen.

Way Forward: Beherrschen Sie die Konzepte der Statistik für eine Karriere in Data Science oder maschinellem Lernen

Die höhere EdTech-Lernplattform von upGrad hat mit ihrer Fülle an Kursen und immersiven Lernerfahrungen über 500.000 Berufstätige weltweit beeinflusst. Mit einer Basis von mehr als 40.000 Lernenden in über 85 Ländern werden die branchenrelevanten Kurse von upGrad Ihre Karriere in dem Bereich Ihrer Wahl garantiert voranbringen.

Der Master of Science in Data Science ist ein 18-monatiger Kurs, der Schlüsselkompetenzen in Statistik, prädiktiver Analyse, maschinellem Lernen, Big Data Analytics, Datenvisualisierung usw. vermittelt.

Programm-Highlights:

• Master-Abschluss von der Liverpool John Moores University und Executive PGP vom IIIT Bangalore
• Über 500 Stunden Inhalt, über 60 Fallstudien und Projekte, über 20 Live-Sitzungen, über 14 Programmiersprachen und Tools
• Branchennetzwerke, Sitzungen zur Zweifelslösung und Lernunterstützung

Das Advanced Certificate Program in Machine Learning und Deep Learning ist ein strenger 6-monatiger Kurs mit Peer-Networking-Möglichkeiten, praktischen Projekten, Branchen-Mentoring und 360-Grad-Karriereunterstützung.

Programm-Highlights:

• Prestigeträchtige Anerkennung von IIIT Bangalore
• Über 240 Stunden Inhalt, über 5 Fallstudien und Projekte, über 24 Live-Sitzungen, Abdeckung von 12 Programmiersprachen, Tools und Bibliotheken
• 1:8-Gruppen-Coaching-Sitzungen und 1:1-Mentoring-Sitzungen mit Branchenexperten

Fazit

Bayesianisches Denken untermauert mehrere Bereiche des menschlichen Denkens, Forschens und Glaubens, auch wenn die meisten von uns sich dessen nicht bewusst sind. Von der Krebsvorsorge und der globalen Erwärmung bis hin zur Geldpolitik und Risikobewertung und Versicherung ist Bayes'sches Denken von grundlegender Bedeutung. Sogar der berühmte britische Mathematiker Alan Turing soll den Bayesschen Ansatz verwendet haben, um den deutschen Enigma-Code während des Zweiten Weltkriegs zu knacken.

Melden Sie sich bei upGrad an und vertiefen Sie Ihr Wissen über wichtige statistische Konzepte und mehr!