Börsenvorhersage mit maschinellem Lernen [Schritt-für-Schritt-Implementierung]
Veröffentlicht: 2021-02-26Inhaltsverzeichnis
Einführung
Vorhersagen und Analysen des Aktienmarktes gehören zu den kompliziertesten Aufgaben. Dafür gibt es mehrere Gründe, wie die Marktvolatilität und so viele andere abhängige und unabhängige Faktoren, die den Wert einer bestimmten Aktie auf dem Markt bestimmen. Diese Faktoren machen es jedem Börsenanalysten sehr schwer, den Anstieg und Fall mit hoher Genauigkeit vorherzusagen.
Mit dem Aufkommen des maschinellen Lernens und seiner robusten Algorithmen haben die neuesten Marktanalyse- und Aktienmarktvorhersage-Entwicklungen jedoch begonnen, solche Techniken in das Verständnis der Aktienmarktdaten einzubeziehen.
Kurz gesagt, Algorithmen des maschinellen Lernens werden von vielen Unternehmen in großem Umfang zur Analyse und Vorhersage von Aktienwerten eingesetzt. In diesem Artikel wird eine einfache Implementierung der Analyse und Vorhersage der Aktienwerte eines beliebten weltweiten Online-Einzelhandelsgeschäfts unter Verwendung mehrerer maschineller Lernalgorithmen in Python beschrieben.
Problemstellung
Bevor wir uns mit der Implementierung des Programms zur Vorhersage der Börsenwerte befassen, lassen Sie uns die Daten visualisieren, an denen wir arbeiten werden. Hier werden wir den Aktienwert der Microsoft Corporation (MSFT) von der National Association of Securities Dealers Automated Quotations (NASDAQ) analysieren. Die Aktienwertdaten werden in Form einer kommagetrennten Datei (.csv) dargestellt, die mit Excel oder einer Tabellenkalkulation geöffnet und angezeigt werden kann.
MSFT hat seine Aktien an der NASDAQ registriert und seine Werte werden an jedem Börsentag aktualisiert. Beachten Sie, dass der Markt samstags und sonntags keinen Handel zulässt; daher gibt es eine Lücke zwischen den beiden Daten. Für jedes Datum werden der Eröffnungswert der Aktie, der höchste und der niedrigste Wert dieser Aktie an denselben Tagen zusammen mit dem Schlusswert am Ende des Tages notiert.
Der angepasste Schlusskurs zeigt den Wert der Aktie nach der Verbuchung der Dividenden (zu technisch!). Darüber hinaus wird auch das Gesamtvolumen der Aktien auf dem Markt angegeben. Mit diesen Daten obliegt es der Arbeit eines Machine Learning/Data Scientist, die Daten zu untersuchen und mehrere Algorithmen zu implementieren, die Muster aus der Historie der Aktien der Microsoft Corporation extrahieren können Daten.

Langes Kurzzeitgedächtnis
Um ein maschinelles Lernmodell zur Vorhersage der Aktienkurse der Microsoft Corporation zu entwickeln, werden wir die Technik des Long Short-Term Memory (LSTM) verwenden. Sie werden verwendet, um kleine Änderungen an den Informationen durch Multiplikationen und Additionen vorzunehmen. Per Definition ist das Langzeitgedächtnis (LSTM) eine künstliche rekurrente neuronale Netzwerkarchitektur (RNN), die beim Deep Learning verwendet wird.
Im Gegensatz zu standardmäßigen neuronalen Feed-Forward-Netzwerken verfügt LSTM über Feedback-Verbindungen. Es kann einzelne Datenpunkte (z. B. Bilder) und ganze Datenfolgen (z. B. Sprache oder Video) verarbeiten. Um das Konzept hinter LSTM zu verstehen, nehmen wir ein einfaches Beispiel einer Online-Kundenbewertung eines Mobiltelefons.
Angenommen, wir möchten das Handy kaufen, verweisen wir in der Regel auf die Netzbewertungen von zertifizierten Nutzern. Abhängig von ihren Überlegungen und Eingaben entscheiden wir, ob das Handy gut oder schlecht ist, und kaufen es dann. Während wir die Rezensionen lesen, suchen wir nach Schlüsselwörtern wie „fantastisch“, „gute Kamera“, „bester Akku-Backup“ und vielen anderen Begriffen, die sich auf ein Mobiltelefon beziehen.
Wir neigen dazu, die im Englischen gebräuchlichen Wörter wie „it“, „gave“, „this“ usw. zu ignorieren. Wenn wir also entscheiden, ob wir das Mobiltelefon kaufen oder nicht, erinnern wir uns nur an diese oben definierten Schlüsselwörter. Höchstwahrscheinlich vergessen wir die anderen Wörter.
Auf die gleiche Weise funktioniert der Algorithmus für das lange Kurzzeitgedächtnis. Es merkt sich nur die relevanten Informationen und verwendet sie, um Vorhersagen zu treffen, wobei die nicht relevanten Daten ignoriert werden. Auf diese Weise müssen wir ein LSTM-Modell aufbauen, das im Wesentlichen nur die wesentlichen Daten über diese Aktie erkennt und ihre Ausreißer auslässt.
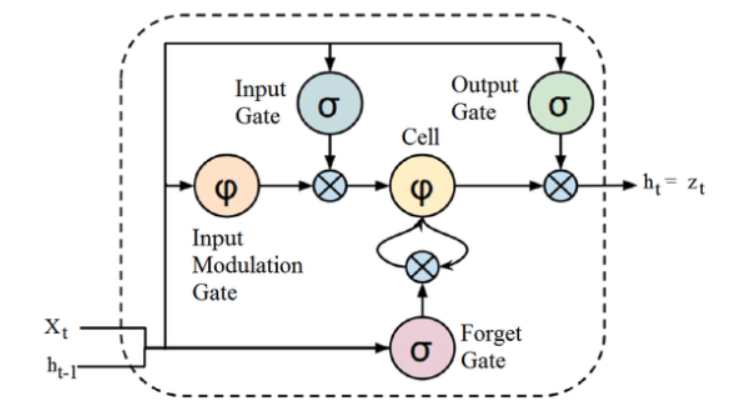
Quelle
Obwohl die oben angegebene Struktur einer LSTM-Architektur auf den ersten Blick faszinierend erscheinen mag, reicht es aus, sich daran zu erinnern, dass LSTM eine erweiterte Version von Recurrent Neural Networks ist, die Speicher behält, um Datensequenzen zu verarbeiten. Es kann Informationen aus dem Zellzustand entfernen oder hinzufügen, sorgfältig reguliert durch Strukturen, die Gates genannt werden.
Die LSTM-Einheit umfasst eine Zelle, ein Eingangsgatter, ein Ausgangsgatter und ein Vergessensgatter. Die Zelle merkt sich Werte über beliebige Zeitintervalle, und die drei Tore regulieren den Informationsfluss in die und aus der Zelle.
Programmimplementierung
Wir werden mit dem Teil fortfahren, in dem wir das LSTM bei der Vorhersage des Aktienwerts mithilfe von maschinellem Lernen in Python einsetzen.
Schritt 1 – Importieren der Bibliotheken
Wie wir alle wissen, besteht der erste Schritt darin, Bibliotheken zu importieren, die für die Vorverarbeitung der Bestandsdaten der Microsoft Corporation und der anderen erforderlichen Bibliotheken zum Erstellen und Visualisieren der Ausgaben des LSTM-Modells erforderlich sind. Dazu verwenden wir die Keras-Bibliothek unter dem TensorFlow-Framework. Die benötigten Module werden einzeln aus der Keras-Bibliothek importiert.
#Importieren der Bibliotheken
Pandas als PD importieren
importiere NumPy als np
%matplotlib inline
matplotlib importieren. Pyplot als plt
matplotlib importieren
von sklearn. Import von MinMaxScaler vorverarbeiten
von Keras. Ebenen importieren LSTM, Dense, Dropout
aus sklearn.model_selection import TimeSeriesSplit
aus sklearn.metrics import mean_squared_error, r2_score
matplotlib importieren. Termine als Mandate
von sklearn. Import von MinMaxScaler vorverarbeiten
aus sklearn import linear_model
von Keras. Modelle importieren sequentiell
von Keras. Ebenen importieren dicht
Keras importieren. Backend als K
von Keras. Callbacks importieren EarlyStopping
von Keras. Optimierer importieren Adam
von Keras. Modelle importieren load_model
von Keras. Ebenen importieren LSTM
von Keras. utils.vis_utils import plot_model
Schritt 2 – Visualisieren der Daten
Mithilfe der Pandas Data Reader-Bibliothek laden wir die Bestandsdaten des lokalen Systems als CSV-Datei (Comma Separated Value) hoch und speichern sie in einem Pandas DataFrame. Abschließend sehen wir uns auch die Daten an.
#Datensatz abrufen
df = pd.read_csv("MicrosoftStockData.csv",na_values=['null'],index_col='Datum',parse_dates=True,infer_datetime_format=True)
df.head()
Holen Sie sich online eine KI-Zertifizierung von den besten Universitäten der Welt – Master, Executive Post Graduate Programs und Advanced Certificate Program in ML & KI, um Ihre Karriere zu beschleunigen.
Schritt 3 – Drucken Sie die DataFrame-Form und prüfen Sie auf Nullwerte.
In diesem weiteren entscheidenden Schritt drucken wir zunächst die Form des Datensatzes. Um sicherzustellen, dass der Datenrahmen keine Nullwerte enthält, prüfen wir sie. Das Vorhandensein von Nullwerten im Datensatz verursacht tendenziell Probleme während des Trainings, da sie als Ausreißer wirken und eine große Varianz im Trainingsprozess verursachen.
#Datenrahmenform drucken und auf Nullwerte prüfen
print("Dataframe Shape: ", df. Form)
print("Nullwert vorhanden: ", df.IsNull().values.any())
>> Datenrahmenform: (7334, 6)
>>Nullwert vorhanden: Falsch
| Datum | Offen | Hoch | Niedrig | Nah dran | Adj Schließen | Volumen |
| 1990-01-02 | 0,605903 | 0,616319 | 0,598090 | 0,616319 | 0,447268 | 53033600 |
| 1990-01-03 | 0,621528 | 0,626736 | 0,614583 | 0,619792 | 0,449788 | 113772800 |
| 1990-01-04 | 0,619792 | 0,638889 | 0,616319 | 0,638021 | 0,463017 | 125740800 |
| 1990-01-05 | 0,635417 | 0,638889 | 0,621528 | 0,622396 | 0,451678 | 69564800 |
| 08.01.1990 | 0,621528 | 0,631944 | 0,614583 | 0,631944 | 0,458607 | 58982400 |
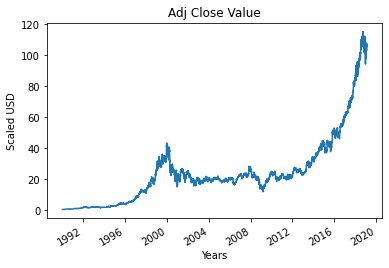
Schritt 4 – Plotten des True Adjusted Close Value
Der endgültige Ausgabewert, der mithilfe des maschinellen Lernmodells vorhergesagt werden soll, ist der angepasste Schlusswert. Dieser Wert stellt den Schlusswert der Aktie an diesem bestimmten Börsenhandelstag dar.
#Zeichnen Sie den True Adj Close-Wert
df['Adj Close'].plot()
Schritt 5 – Festlegen der Zielvariablen und Auswählen der Funktionen
Im nächsten Schritt weisen wir die Ausgabespalte der Zielvariablen zu. In diesem Fall ist es der bereinigte relative Wert der Microsoft-Aktie. Zusätzlich wählen wir auch die Merkmale aus, die als unabhängige Variable zur Zielvariablen (abhängige Variable) fungieren. Um den Trainingszweck zu berücksichtigen, wählen wir vier Merkmale aus:

- Offen
- Hoch
- Niedrig
- Volumen
#Zielvariable setzen
output_var = PD.DataFrame(df['Adj Close'])
#Auswählen der Funktionen
features = ['Offen', 'Hoch', 'Niedrig', 'Lautstärke']
Schritt 6 – Skalierung
Um den Rechenaufwand der Daten in der Tabelle zu reduzieren, werden wir die Bestandswerte auf Werte zwischen 0 und 1 herunterskalieren. Auf diese Weise werden alle Daten in großen Zahlen reduziert, wodurch der Speicherverbrauch reduziert wird. Außerdem können wir durch Herunterskalieren mehr Genauigkeit erzielen, da die Daten nicht in enormen Werten verteilt sind. Dies wird von der MinMaxScaler-Klasse der sci-kit-learn-Bibliothek durchgeführt.
#Skalierung
Scaler = MinMaxScaler()
feature_transform = scaler.fit_transform(df[features])
feature_transform= pd.DataFrame(columns=features, data=feature_transform, index=df.index)
feature_transform.head()
| Datum | Offen | Hoch | Niedrig | Volumen |
| 1990-01-02 | 0,000129 | 0,000105 | 0,000129 | 0,064837 |
| 1990-01-03 | 0,000265 | 0,000195 | 0,000273 | 0,144673 |
| 1990-01-04 | 0,000249 | 0,000300 | 0,000288 | 0,160404 |
| 1990-01-05 | 0,000386 | 0,000300 | 0,000334 | 0,086566 |
| 08.01.1990 | 0,000265 | 0,000240 | 0,000273 | 0,072656 |
Wie oben erwähnt, sehen wir, dass die Werte der Merkmalsvariablen im Vergleich zu den oben angegebenen realen Werten auf kleinere Werte herunterskaliert werden.
Schritt 7 – Aufteilen in einen Trainingssatz und einen Testsatz.
Bevor wir die Daten in das Trainingsmodell einspeisen, müssen wir den gesamten Datensatz in einen Trainings- und einen Testsatz aufteilen. Das LSTM-Modell für maschinelles Lernen wird mit den im Trainingsdatensatz vorhandenen Daten trainiert und im Testdatensatz auf Genauigkeit und Backpropagation getestet.
Dazu verwenden wir die TimeSeriesSplit-Klasse der sci-kit-learn-Bibliothek. Wir legen die Anzahl der Splits auf 10 fest, was bedeutet, dass 10 % der Daten als Testsatz und 90 % der Daten zum Trainieren des LSTM-Modells verwendet werden. Der Vorteil der Verwendung dieser Zeitreihenaufteilung besteht darin, dass die Datenstichproben der aufgeteilten Zeitreihen in festen Zeitintervallen beobachtet werden.
#Aufteilen in Trainingssatz und Testsatz
timesplit= TimeSeriesSplit(n_splits=10)
für train_index, test_index in timesplit.split(feature_transform):
X_train, X_test = feature_transform[:len(train_index)], feature_transform[len(train_index): (len(train_index)+len(test_index))]
y_train, y_test = output_var[:len(train_index)].values.ravel(), output_var[len(train_index): (len(train_index)+len(test_index))].values.ravel()
Schritt 8 – Verarbeitung der Daten für LSTM
Sobald die Trainings- und Testsätze fertig sind, können wir die Daten in das LSTM-Modell einspeisen, sobald es erstellt ist. Zuvor müssen wir die Trainings- und Testsatzdaten in einen Datentyp konvertieren, den das LSTM-Modell akzeptiert. Wir konvertieren zuerst die Trainingsdaten und Testdaten in NumPy-Arrays und formen sie dann in das Format (Anzahl der Samples, 1, Anzahl der Merkmale) um, da das LSTM erfordert, dass die Daten in 3D-Form zugeführt werden. Wie wir wissen, beträgt die Anzahl der Stichproben im Trainingssatz 90 % von 7334, was 6667 entspricht, und die Anzahl der Merkmale 4, der Trainingssatz wird umgeformt zu (6667, 1, 4). In ähnlicher Weise wird auch das Testset umgestaltet.
#Daten für LSTM verarbeiten
trainX =np.array(X_train)
testX =np.array(X_test)
X_train = trainX.reshape(X_train.shape[0], 1, X_train.shape[1])
X_test = testX.reshape(X_test.form[0], 1, X_test.form[1])
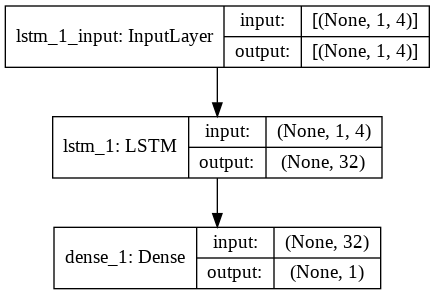
Schritt 9 – Erstellen des LSTM-Modells
Schließlich kommen wir zu der Phase, in der wir das LSTM-Modell erstellen. Hier erstellen wir ein sequenzielles Keras-Modell mit einer LSTM-Schicht. Die LSTM-Schicht hat 32 Einheiten, und ihr folgt eine dichte Schicht aus 1 Neuron.
Wir verwenden Adam Optimizer und den Mean Squared Error als Verlustfunktion zum Kompilieren des Modells. Diese beiden sind die am meisten bevorzugte Kombination für ein LSTM-Modell. Zusätzlich wird das Modell auch geplottet und unten angezeigt.
#Aufbau des LSTM-Modells
lstm = sequentiell ()
lstm.add(LSTM(32, input_shape=(1, trainX.shape[1]), activation='relu', return_sequences=False))
lstm.add (dicht (1))
lstm.compile(loss='mean_squared_error', optimizer='adam')
plot_model(lstm, show_shapes=True, show_layer_names=True)
Schritt 10 – Modell trainieren
Schließlich trainieren wir das oben entworfene LSTM-Modell auf den Trainingsdaten für 100 Epochen mit einer Stapelgröße von 8 unter Verwendung der Fit-Funktion.
#Modeltraining
history = lstm.fit(X_train, y_train, epochs=100, batch_size=8, verbose=1, shuffle=False)
Epoche 1/100
834/834 [==============================] – 3s 2ms/Schritt – Verlust: 67.1211
Epoche 2/100
834/834 [==============================] – 1s 2ms/Schritt – Verlust: 70.4911
Epoche 3/100
834/834 [==============================] – 1s 2ms/Schritt – Verlust: 48.8155
Epoche 4/100
834/834 [==============================] – 1s 2ms/Schritt – Verlust: 21.5447
Epoche 5/100
834/834 [==============================] – 1s 2ms/Schritt – Verlust: 6.1709
Epoche 6/100
834/834 [==============================] – 1s 2ms/Schritt – Verlust: 1,8726
Epoche 7/100
834/834 [==============================] – 1s 2ms/Schritt – Verlust: 0,9380
Epoche 8/100
834/834 [==============================] – 2s 2ms/Schritt – Verlust: 0,6566
Epoche 9/100
834/834 [==============================] – 1s 2ms/Schritt – Verlust: 0,5369
Epoche 10/100
834/834 [==============================] – 2s 2ms/Schritt – Verlust: 0,4761
.
.
.
.
Epoche 95/100
834/834 [==============================] – 1s 2ms/Schritt – Verlust: 0,4542
Epoche 96/100
834/834 [==============================] – 2s 2ms/Schritt – Verlust: 0,4553
Epoche 97/100
834/834 [==============================] – 1s 2ms/Schritt – Verlust: 0,4565
Epoche 98/100
834/834 [==============================] – 1s 2ms/Schritt – Verlust: 0,4576
Epoche 99/100
834/834 [==============================] – 1s 2ms/Schritt – Verlust: 0,4588
Epoche 100/100
834/834 [==============================] – 1s 2ms/Schritt – Verlust: 0,4599
Schließlich sehen wir, dass der Verlustwert über die Zeit während des Trainingsprozesses von 100 Epochen exponentiell abgenommen hat und einen Wert von 0,4599 erreicht hat
Schritt 11 – LSTM-Vorhersage
Wenn unser Modell fertig ist, ist es an der Zeit, das mit dem LSTM-Netzwerk trainierte Modell auf dem Testset zu verwenden und den Adjacent Close Value der Microsoft-Aktie vorherzusagen. Dies wird durch Verwenden der einfachen Funktion von Predict auf dem erstellten LSTM-Modell durchgeführt.
#LSTM-Vorhersage
y_pred= lstm.predict(X_test)
Schritt 12 – True vs Predicted Adj Close Value – LSTM
Nachdem wir die Werte des Testsets vorhergesagt haben, können wir schließlich das Diagramm darstellen, um sowohl die wahren Werte von Adj Close als auch den vorhergesagten Wert von Adj Close durch das LSTM-Modell für maschinelles Lernen zu vergleichen.
#True vs. Predicted Adj Close Value – LSTM
plt.plot(y_test, label='Wahrer Wert')
plt.plot(y_pred, label='LSTM-Wert')
plt.title („Vorhersage von LSTM“)
plt.xlabel('Zeitskala')

plt.ylabel('Skalierter USD')
plt.legend()
plt.show()
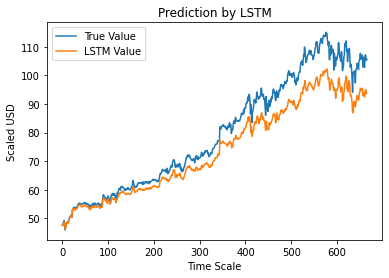
Das obige Diagramm zeigt, dass einige Muster von dem oben erstellten sehr einfachen Einzel-LSTM-Netzwerkmodell erkannt werden. Durch die Feinabstimmung mehrerer Parameter und das Hinzufügen weiterer LSTM-Schichten zum Modell können wir eine genauere Darstellung des Aktienwerts eines bestimmten Unternehmens erreichen.
Fazit
Wenn Sie mehr über Beispiele für künstliche Intelligenz und maschinelles Lernen erfahren möchten, sehen Sie sich das Executive PG-Programm von IIIT-B & upGrad für maschinelles Lernen und KI an, das für Berufstätige konzipiert ist und mehr als 450 Stunden strenge Schulungen und mehr als 30 Fallstudien bietet & Aufgaben, IIIT-B-Alumni-Status, mehr als 5 praktische, praktische Abschlussprojekte und Arbeitsunterstützung bei Top-Unternehmen.
Können Sie den Aktienmarkt mit maschinellem Lernen vorhersagen?
Heute verfügen wir über eine Reihe von Indikatoren, mit denen sich Markttrends vorhersagen lassen. Wir müssen jedoch nicht weiter als einen Hochleistungscomputer suchen, um die genauesten Indikatoren für den Aktienmarkt zu finden. Die Börse ist ein offenes System und kann als komplexes Netzwerk betrachtet werden. Das Netzwerk besteht aus den Beziehungen zwischen den Aktien, Unternehmen, Investoren und Handelsvolumina. Durch die Verwendung eines Data-Mining-Algorithmus wie der Support Vector Machine können Sie eine mathematische Formel anwenden, um die Beziehungen zwischen diesen Variablen zu extrahieren. Der Aktienmarkt ist jetzt jenseits menschlicher Vorhersagen.
Welcher Algorithmus eignet sich am besten für die Börsenprognose?
Für beste Ergebnisse sollten Sie die lineare Regression verwenden. Die lineare Regression ist ein statistischer Ansatz, der verwendet wird, um die Beziehung zwischen zwei verschiedenen Variablen zu bestimmen. In diesem Beispiel sind die Variablen Preis und Zeit. Bei der Börsenprognose ist der Preis die unabhängige Variable und die Zeit die abhängige Variable. Wenn eine lineare Beziehung zwischen diesen beiden Variablen festgestellt werden kann, ist es möglich, den Wert der Aktie zu jedem Zeitpunkt in der Zukunft genau vorherzusagen.
Ist die Börsenvorhersage ein Klassifikations- oder Regressionsproblem?
Bevor wir antworten, müssen wir verstehen, was Börsenprognosen bedeuten. Handelt es sich um ein binäres Klassifikationsproblem oder um ein Regressionsproblem? Angenommen, wir möchten die Zukunft einer Aktie vorhersagen, wobei Zukunft den nächsten Tag, die nächste Woche, den nächsten Monat oder das nächste Jahr bedeutet. Wenn die vergangene Wertentwicklung der Aktie zu einem bestimmten Zeitpunkt der Input und die Zukunft der Output ist, dann handelt es sich um ein Regressionsproblem. Wenn die Wertentwicklung einer Aktie in der Vergangenheit und die Zukunft einer Aktie unabhängig voneinander sind, handelt es sich um ein Klassifizierungsproblem.
