Erste Schritte mit der negativen binomialen Regression: Schritt-für-Schritt-Anleitung
Veröffentlicht: 2022-04-17Zur Modellierung von Zählvariablen wird die Technik der Negativen Binomialen Regression verwendet. Die Methode ähnelt fast der multiplen Regressionsmethode. Allerdings gibt es den Unterschied, dass bei der negativen Binomialregression die abhängige Variable, also Y, der negativen Binomialverteilung folgt. Daher können die Werte der Variablen nicht negative ganze Zahlen wie 0, 1, 2 sein.
Die Methode ist auch eine Erweiterung der Poisson-Regression, bei der angenommen wird, dass der Mittelwert gleich der Varianz ist. Eines der traditionellen Modelle der binomialen Regression, definiert als „NB2“, basiert auf der gemischten Verteilung von Poisson-Gamma.
Das Verfahren der Poisson-Regression wird verallgemeinert, indem eine Variable des Gammarauschens hinzugefügt wird. Diese Variable hat einen Mittelwert von eins und auch einen Skalenparameter, der „v“ ist.
Hier sind einige Beispiele für die negative binomiale Regression:
- Die Schulleitung führte eine Studie durch, um das Besuchsverhalten der Gymnasiasten zweier Schulen zu untersuchen. Zu den Faktoren, die das Anwesenheitsverhalten beeinflussen könnten, könnten die Tage gehören, an denen die Junioren von der Schule abwesend waren. Auch das Programm, in dem sie eingeschrieben waren.
- Ein Forscher einer gesundheitsbezogenen Studie hat untersucht, wie viele Senioren in den letzten 12 Monaten ein Krankenhaus besucht haben. Die Studie basierte auf den Merkmalen der Person und den Gesundheitsplänen, die die Senioren kauften.
Beispiel für negative binomiale Regression
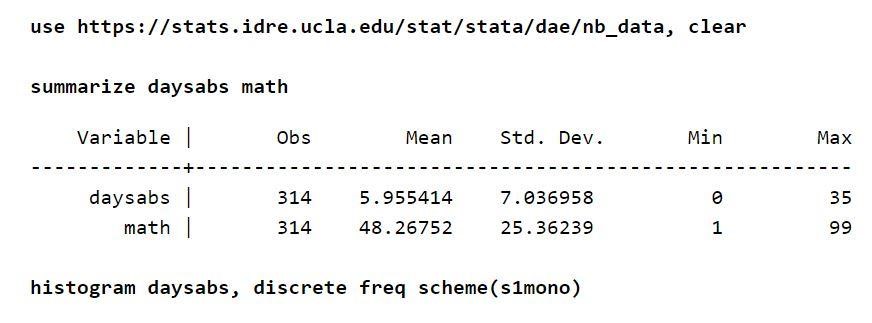
Angenommen, es gibt eine Anwesenheitsliste von etwa 314 Schülern der High School. Die Daten stammen von zwei städtischen Schulen und werden in einer Datei namens nb_data.dta gespeichert. Die interessante Antwortvariable in diesem Beispiel sind die Abwesenheitstage, die „daysabs“ sind. Eine Variable, „math“, ist vorhanden, die die Mathematikpunktzahl für jeden Schüler definiert. Es gibt eine weitere Variable, die „prog“ ist. Diese Variable gibt das Programm an, in dem die Studenten eingeschrieben sind.
Quelle

Jede der Variablen hat etwa 314 Beobachtungen. Daher sind auch die Verteilungen auf die Variablen sinnvoll. Auch unter Berücksichtigung der Ergebnisvariablen ist der unbedingte Mittelwert niedriger als die Varianz.
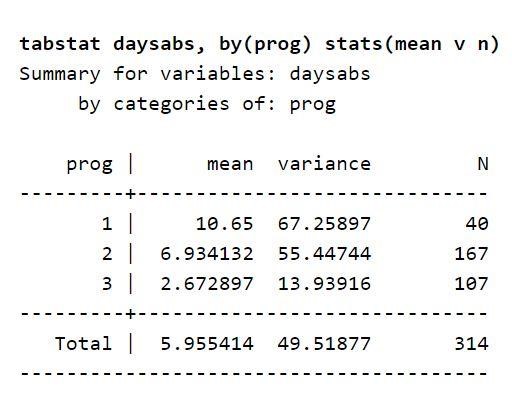
Konzentrieren Sie sich nun auf die im Datensatz betrachtete Variablenbeschreibung. Eine Tabelle listet die durchschnittlichen Tage auf, die ein Schüler in jedem Programmtyp von der Schule abwesend war. Dies legt nahe, dass das Programm vom variablen Typ die Tage vorhersagen kann, an denen der Schüler von der Schule abwesend war. Sie können es auch zur Vorhersage der Ergebnisvariablen verwenden. Dies liegt daran, dass der Mittelwert für die Ergebnisvariable um die Variable prog variiert. Außerdem sind die Werte der Varianzen höher als in jeder Ebene der Variablen prog. Diese Werte werden Varianzen und Mittelwerte genannt. Die bestehenden Unterschiede legen nahe, dass eine Überdispersion vorliegt, und daher ist es angemessen, ein negatives Binomialmodell zu verwenden.
Quelle
Ein Forscher kann mehrere Analysemethoden für diese Art von Studie in Betracht ziehen. Diese Methoden werden unten beschrieben. Einige der Analysemethoden, die der Benutzer zur Analyse des Regressionsmodells verwenden kann, sind:
1. Negative binomiale Regression
Bei überstreuten Daten ist die Methode der negativen binomialen Regression anzuwenden. Dies bedeutet, dass der Wert der bedingten Varianz höher ist oder den Wert des bedingten Mittelwerts übersteigt. Das Verfahren wird als von der Poisson-Regressionsmethode verallgemeinert angesehen. Dies liegt daran, dass beide Methoden die gleiche Struktur des Mittelwerts haben. Es gibt jedoch einen zusätzlichen Parameter in der negativen binomialen Regression, der zum Modellieren der Überdispersion verwendet wird. Die Konfidenzintervalle gelten als enger als die Leidenschaftsregression, wenn die bedingte Verteilung von der Ergebnisvariablen zu stark gestreut ist.
2. Poisson-Regression
Bei der Modellierung der Zähldaten wird die Methode der Poisson-Regression verwendet. Viele Erweiterungen können zur Modellierung der Zählvariablen in der Poisson-Regression verwendet werden.
3. OLS-Regression
Die Ergebnisse der Zählvariablen werden manchmal log-transformiert und dann mit der Methode der OLS-Regression analysiert. Es gibt jedoch manchmal Probleme im Zusammenhang mit der Methode der OLS-Regression. Diese Probleme können der Datenverlust aufgrund der Generierung eines undefinierten Werts durch Berücksichtigung des Protokolls des Werts Null sein. Es kann auch aufgrund des Fehlens einer Modellierung der verteilten Daten generiert werden.
4. Null aufgepumpte Modelle
Diese Arten von Modellen versuchen, alle überschüssigen Nullen im Modell zu berücksichtigen.
Analyse mit der negativen binomialen Regression
Der Befehl „nbreg“ wird zum Schätzen des Modells der negativen binomialen Regression verwendet. Vor der Variable „prog“ steht ein „i“. Das Vorhandensein von „i“ zeigt an, dass die Variable vom Typ Faktor ist, dh eine kategoriale Variable. Diese sollten als Indikatorvariablen in das Modell aufgenommen werden.

- Die Ausgabe des Modells beginnt mit einem Iterationsprotokoll. Es beginnt mit der Anpassung des Modells von Poisson, gefolgt von einem Nullmodell und dann dem Modell des negativen Binoms. Das Verfahren verwendet die Schätzung der maximalen Wahrscheinlichkeit und iteriert weiter, bis sich der Wert des endgültigen Protokolls ändert. Die Wahrscheinlichkeit des Protokolls wird für den Vergleich der Modelle verwendet.
- Die nächste Information befindet sich in der Header-Datei.
- Direkt unter der Kopfzeile befinden sich die Informationen zu den Koeffizienten der negativen binomialen Regression. Die Koeffizienten werden für jede Variable zusammen mit den Fehlern wie p-Werten, z-Scores generiert. Außerdem gibt es für alle Koeffizienten ein Konfidenzintervall von 95 %. Der Koeffizient für die Variable „Mathematik“ beträgt -0,006, was bedeutet, dass sie statistisch signifikant ist. Das Ergebnis bedeutet, dass bei einer Erhöhung der Variablen „math“ um eine Einheit die erwartete Protokollanzahl für die fehlende Anzahl von Tagen um einen Wert von 0,006 abnimmt. Außerdem ist der Wert der 2. prog, der Indikatorvariable, die erwartete Differenz in der Zählung von log zwischen den zwei Gruppen (Gruppe 2 und Referenzgruppe).
- Die Parameterschätzung für die logarithmisch übertragene Überdispersion wird durchgeführt und dann mit dem untransformierten Wert angezeigt. Im Poisson-Modell ist der Wert Null.
- Unterhalb der Koeffiziententabelle befindet sich eine Ratio-Test-Wahrscheinlichkeitsinformation. Das Modell kann durch die Verwendung der Befehle „Ränder“ weiter verstanden werden.
Prozess zur Durchführung einer negativen binomialen Regressionsanalyse in Python
Die erforderlichen Pakete zur Durchführung des Regressionsprozesses müssen aus Python importiert werden. Diese Pakete sind unten aufgeführt:

- importiere statsmodels.api als sm
- importiere matplotlib.pyplot als plt
- importiere numpy als np
- von patsy import dmatrices
- pandas als pd importieren
Überlegungen zur negativen binomialen Regression
Es gibt ein paar Dinge, die bei der Anwendung der Methode der negativen binomialen Regressionsanalyse berücksichtigt werden sollten. Diese beinhalten:
- Wenn kleine Stichproben vorhanden sind, wird die Methode der negativen binomialen Regression nicht empfohlen.
- Manchmal sind überschüssige Nullen vorhanden, was eine Ursache für die Überdispersion sein könnte. Diese Nullen können aufgrund des Prozesses des Hinzufügens der Datengenerierung generiert werden. Tritt ein solcher Fall ein, empfiehlt es sich, die Methode des Zero-Inflated-Modells anzuwenden.
- Berücksichtigt der Prozess der Datengenerierung keine Nullstellen, so empfiehlt sich in solchen Fällen die Anwendung der Methode des Zero-Truncated-Modells.
- Den Zähldaten ist eine Belichtungsvariable zugeordnet. Die Variable bezeichnet die Zeiten, zu denen eine Chance besteht, dass das Ereignis eintreten kann. Diese Variable muss in das Modell der negativen binomialen Regression aufgenommen werden. Dies geschieht über die Option von exp().
- Die Ergebnisvariable darf im Modell der negativen binomialen Regressionsanalyse kein negativer Wert sein. Außerdem darf die Exposure-Variable nicht den Wert 0 haben.
- Der Befehl „glm“ kann auch zum Ausführen einer Analysemethode der negativen binomialen Regression verwendet werden. Dies kann über den Link des Protokolls und auch der Binomialfamilie erfolgen.
- Um die Residuen zu erhalten, ist der Befehl „glm“ erforderlich. Damit soll überprüft werden, ob es andere Annahmen im Modell der negativen binomialen Regression gibt.
- Es gibt die verschiedenen Maße des Pseudo-R-Quadrats. Jedes Maß liefert jedoch ähnliche Informationen wie das R-Quadrat in der Regression von OLS.
Fazit
Der Artikel befasste sich mit dem Thema der negativen binomialen Regression . Wir haben gesehen, dass es der Methode der multiplen Regression fast ähnlich ist und eine verallgemeinerte Form der Poisson-Verteilung ist. Es gibt mehrere Anwendungen der Methode. Die Technik kann auch über die Programmiersprache Python oder in R angewendet werden.
Es sind auch mehrere Fallstudien vorhanden, die ihre Anwendung in Studien wie dem Altern zeigen. Die klassischen Regressionsmodelle, die für die Zähldaten verwendet werden können, sind die Poisson-Regression, die negative binomiale Regression und die geometrische Regression. Diese Methoden gehörten zur Familie der linearen Modelle und waren in fast allen Statistikpaketen wie dem R-System enthalten.
Wenn Sie sich im maschinellen Lernen auszeichnen und das Feld der Daten erkunden möchten, können Sie den von upGrad angebotenen Kurs Executive PG Program in Machine Learning & AI besuchen. Wenn Sie also ein Berufstätiger sind, der davon träumt, ein Experte für maschinelles Lernen zu werden, kommen Sie und sammeln Sie die Erfahrung, sich von Experten ausbilden zu lassen. Weitere Details können über unsere Website erreicht werden. Bei Fragen hilft Ihnen unser Team umgehend weiter.