7 am häufigsten verwendete Algorithmen für maschinelles Lernen in Python, die Sie kennen sollten

Maschinelles Lernen ist ein Zweig der künstlichen Intelligenz (KI), der sich mit den Computeralgorithmen befasst, die auf beliebige Daten angewendet werden. Es konzentriert sich darauf, automatisch aus den eingegebenen Daten zu lernen, und es liefert uns Ergebnisse, indem es die vorherigen Vorhersagen jedes Mal verbessert.

Top-Algorithmen für maschinelles Lernen, die in Python verwendet werden

Nachfolgend finden Sie einige der wichtigsten in Python verwendeten Algorithmen für maschinelles Lernen sowie Codeausschnitte, die ihre Implementierung und Visualisierungen von Klassifizierungsgrenzen zeigen.

1. Lineare Regression

Die lineare Regression ist eine der am häufigsten verwendeten Techniken des überwachten maschinellen Lernens. Wie der Name schon sagt, versucht diese Regression, die Beziehung zwischen zwei Variablen mithilfe einer linearen Gleichung zu modellieren und diese Linie an die beobachteten Daten anzupassen. Diese Technik wird verwendet, um reale kontinuierliche Werte wie den Gesamtumsatz oder die Kosten von Häusern zu schätzen.

Die Ausgleichsgerade wird auch als Regressionsgerade bezeichnet. Sie ist durch die folgende Gleichung gegeben:

Y = a*X + b

Dabei ist Y die abhängige Variable, a die Steigung, X die unabhängige Variable und b der Schnittpunktwert. Die Koeffizienten a und b werden durch Minimieren des Quadrats der Differenz dieses Abstands zwischen den verschiedenen Datenpunkten und der Regressionsliniengleichung abgeleitet.

# synthetischer Datensatz für einfache Regression

aus sklearn.datasets import make_regression

plt.figure()

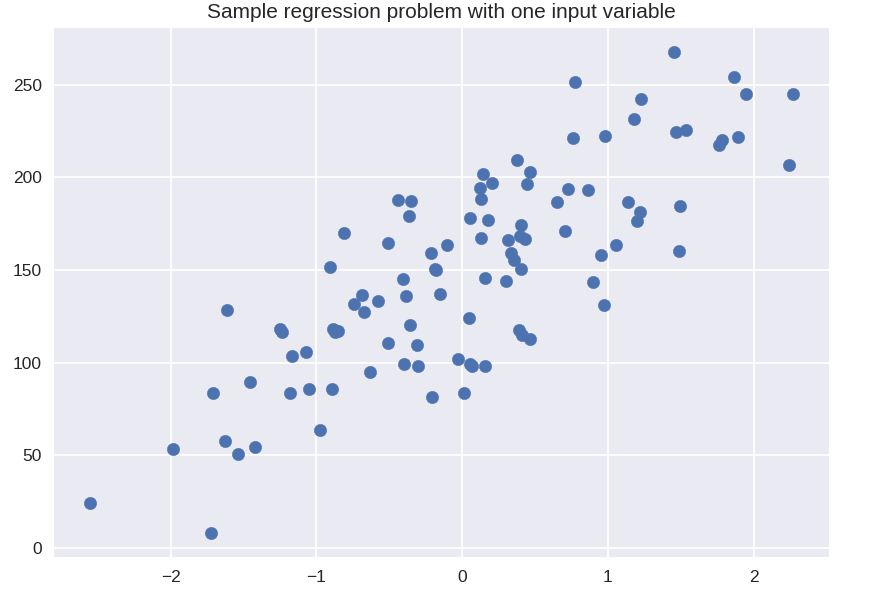
plt.title( 'Beispielregressionsproblem mit einer Eingabevariablen' )

X_R1, y_R1 = make_regression( n_samples = 100, n_features = 1, n_informative = 1, bias = 150.0, noise = 30, random_state = 0 )

plt.scatter( X_R1, y_R1, Marker = 'o', s = 50 )

plt.show()

aus sklearn.linear_model import LinearRegression

X_train, X_test, y_train, y_test = train_test_split( X_R1, y_R1,

random_state = 0 )

linreg = LinearRegression().fit( X_train, y_train )

print( 'linearer Modellkoeffizient (w): {}'.format( linreg.coef_ ) )

print( 'linearer Modellabschnitt (b): {:.3f}'z.format( linreg.intercept_ ) )

print( 'R-Quadrat-Ergebnis (Training): {:.3f}'.format( linreg.score( X_train, y_train ) ) )

print( 'R-Quadrat-Ergebnis (Test): {:.3f}'.format( linreg.score( X_test, y_test ) ) )

Ausgabe

linearer Modellkoeffizient (w): [ 45.71]

linearer Modellabschnitt (b): 148,446

R-Quadrat-Score (Training): 0,679

R-Quadrat-Score (Test): 0,492

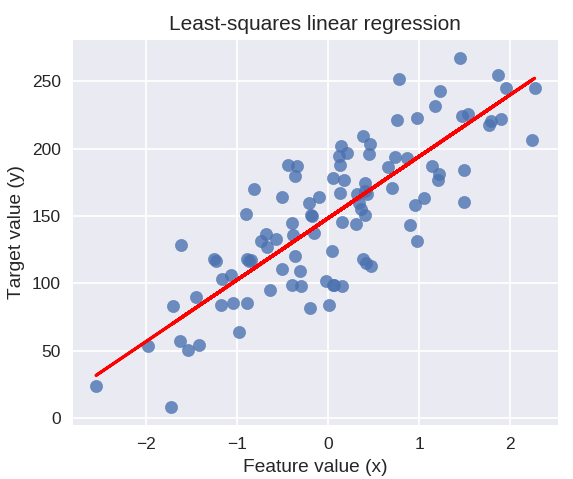
Der folgende Code zeichnet die angepasste Regressionslinie auf dem Diagramm unserer Datenpunkte.

plt.figure( figsize = ( 5, 4 ) )

plt.scatter( X_R1, y_R1, Marker = 'o', s = 50, alpha = 0,8 )

plt.plot( X_R1, linreg.coef_ * X_R1 + linreg.intercept_, 'r-' )

plt.title( 'Lineare Regression der kleinsten Quadrate' )

plt.xlabel( 'Merkmalswert (x)' )

plt.ylabel( 'Zielwert (y)' )

plt.show()

Vorbereiten eines gemeinsamen Datensatzes zum Erkunden von Klassifizierungstechniken

Die folgenden Daten werden verwendet, um die verschiedenen Klassifizierungsalgorithmen zu zeigen, die am häufigsten beim maschinellen Lernen in Python verwendet werden.

Der UCI-Pilzdatensatz wird in mushrooms.csv gespeichert.

%matplotlib-Notizbuch

pandas als pd importieren

importiere numpy als np

importiere matplotlib.pyplot als plt

von sklearn.decomposition import PCA

aus sklearn.model_selection import train_test_split

df = pd.read_csv( 'readonly/mushrooms.csv' )

df2 = pd.get_dummies( df )

df3 = df2.sample( frac = 0,08 )

X = df3.iloc[:, 2:]

y = df3.iloc[:, 1]

pca = PCA( n_Komponenten = 2 ).fit_transform( X )

X_train, X_test, y_train, y_test = train_test_split( pca, y, random_state = 0 )

plt.figure ( dpi = 120 )

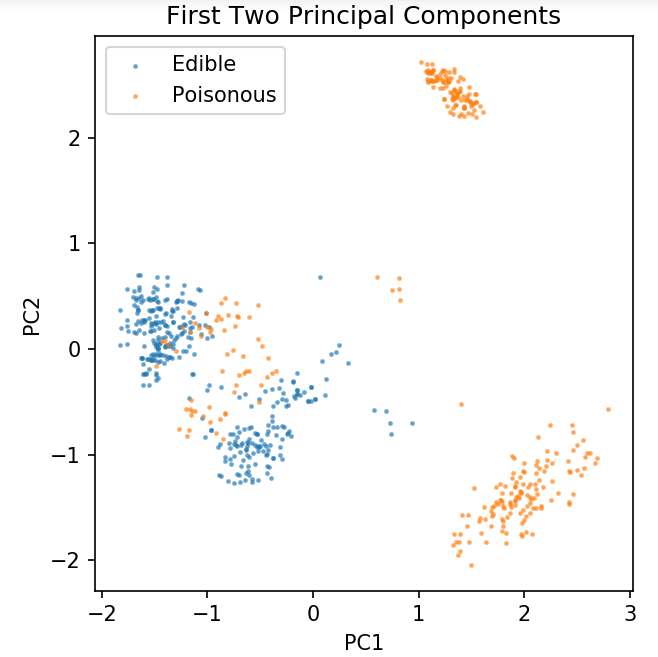
plt.scatter( pca[y.values ​​== 0, 0], pca[y.values ​​== 0, 1], alpha = 0.5, label = 'Essbar', s = 2 )

plt.scatter( pca[y.values ​​== 1, 0], pca[y.values ​​== 1, 1], alpha = 0.5, label = 'Poisonous', s = 2 )

plt.legend()

plt.title( 'Pilzdatensatz\nErste zwei Hauptkomponenten' )

plt.xlabel( 'PC1' )

plt.ylabel( 'PC2' )

plt.gca().set_aspect( 'equal' )

Wir werden die unten definierte Funktion verwenden, um die Entscheidungsgrenzen der verschiedenen Klassifikatoren zu erhalten, die wir für den Pilzdatensatz verwenden werden.

def plot_mushroom_boundary( X, y, angepasstes_modell ):

plt.figure( figsize = (9.8, 5), dpi = 100 )

for i, plot_type in enumerate( ['Entscheidungsgrenze', 'Entscheidungswahrscheinlichkeiten'] ):

plt.subplot( 1, 2, i + 1 )

mesh_step_size = 0.01 # Schrittweite im Mesh

x_min, x_max = X[:, 0].min() – .1, X[:, 0].max() + .1

y_min, y_max = X[:, 1].min() – .1, X[:, 1].max() + .1

xx, yy = np.meshgrid( np.arange( x_min, x_max, mesh_step_size ), np.arange( y_min, y_max, mesh_step_size ) )

wenn ich == 0:

Z = angepasstes_Modell.Vorhersage( np.c_[xx.ravel(), yy.ravel()] )

anders:

Versuchen:

Z = angepasstes_Modell.Vorhersage_Wahrscheinlichkeit( np.c_[xx.ravel(), yy.ravel()] )[:, 1]

außer:

plt.text( 0.4, 0.5, 'Wahrscheinlichkeiten nicht verfügbar', horizontalalignment = 'center', verticalalignment = 'center', transform = plt.gca().transAxes, fontsize = 12 )

plt.axis( 'off' )

brechen

Z = Z.Umformung( xx.Form )

plt.scatter( X[y.values ​​== 0, 0], X[y.values ​​== 0, 1], alpha = 0.4, label = 'Essbar', s = 5 )

plt.scatter( X[y.values ​​== 1, 0], X[y.values ​​== 1, 1], alpha = 0.4, label = 'Posionous', s = 5 )

plt.imshow( Z, interpolation = 'nearest', cmap = 'RdYlBu_r', alpha = 0.15, expansion = ( x_min, x_max, y_min, y_max ), origin = 'lower' )

plt.title( plot_type + '\n' + str( angepasstes_modell ).split( '(' )[0] + ' Testgenauigkeit: ' + str( np.round( angepasstes_modell.score( X, y ), 5 ) ) )

plt.gca().set_aspect( 'equal' );

plt.tight_layout()

plt.subplots_adjust (oben = 0,9, unten = 0,08, wspace = 0,02)

2. Logistische Regression

Im Gegensatz zur linearen Regression befasst sich die logistische Regression mit der Schätzung diskreter Werte (0/1-Binärwerte, wahr/falsch, ja/nein). Diese Technik wird auch Logit-Regression genannt. Dies liegt daran, dass es die Wahrscheinlichkeit eines Ereignisses vorhersagt, indem es eine Logit-Funktion verwendet, um die gegebenen Daten zu trainieren. Sein Wert liegt immer zwischen 0 und 1 (da er eine Wahrscheinlichkeit berechnet).

Die logarithmischen Quoten der Ergebnisse werden wie folgt als lineare Kombination der Prädiktorvariablen konstruiert:

Odds = p / (1 – p) = Wahrscheinlichkeit, dass ein Ereignis eintritt oder Wahrscheinlichkeit, dass ein Ereignis nicht eintritt

ln( Chancen ) = ln( p / (1 – p) )

logit( p ) = ln( p / (1 – p) ) = b0 + b1X1 + b2X2 + b3X3 + … + bkXk

wobei p die Wahrscheinlichkeit des Vorhandenseins eines Merkmals ist.

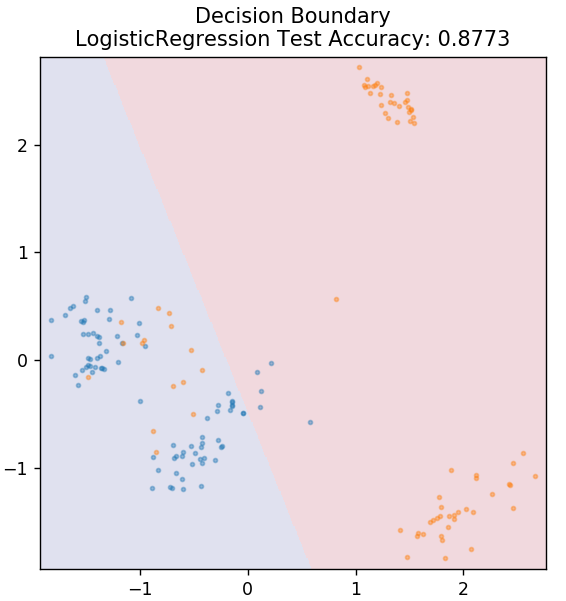
aus sklearn.linear_model import LogisticRegression

model = Logistische Regression ()

model.fit( X_train, y_train )

plot_mushroom_boundary( X_test, y_test, Modell)

Erhalten Sie eine Online- Zertifizierung für künstliche Intelligenz von den besten Universitäten der Welt – Masters, Executive Post Graduate Programs und Advanced Certificate Program in ML & AI, um Ihre Karriere zu beschleunigen.

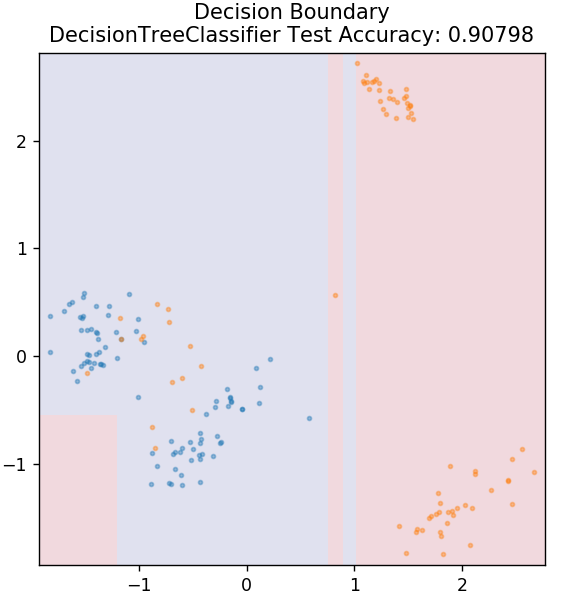
3. Entscheidungsbaum

Dies ist ein sehr beliebter Algorithmus, der verwendet werden kann, um sowohl kontinuierliche als auch diskrete Datenvariablen zu klassifizieren. Bei jedem Schritt werden die Daten basierend auf einigen Aufteilungsattributen/-bedingungen in mehr als einen homogenen Satz aufgeteilt.

aus sklearn.tree import DecisionTreeClassifier

model = DecisionTreeClassifier( max_tiefe = 3 )

model.fit( X_train, y_train )

plot_mushroom_boundary( X_test, y_test, Modell)

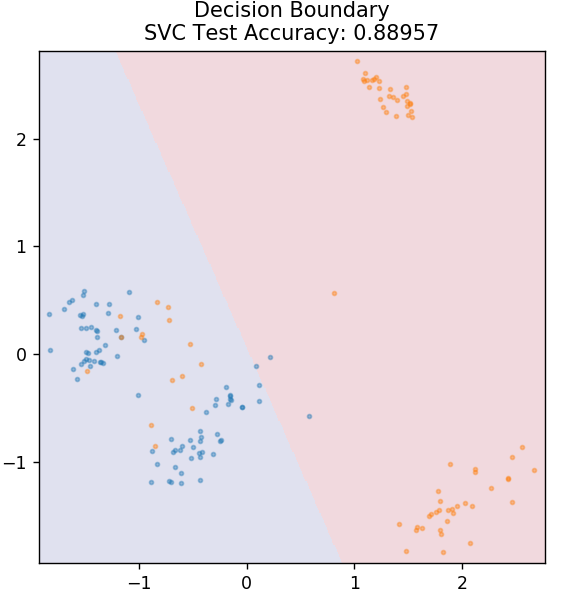
4. SVM

SVM ist die Abkürzung für Support Vector Machines. Hier ist die Grundidee, die Datenpunkte zu klassifizieren, indem Hyperebenen zur Trennung verwendet werden. Das Ziel ist das Finden einer solchen Hyperebene, die den maximalen Abstand (oder Spielraum) zwischen den Datenpunkten beider Klassen oder Kategorien hat.

Wir wählen das Flugzeug so aus, dass wir uns in Zukunft mit höchster Zuversicht um die Klassifizierung unbekannter Punkte kümmern. SVMs werden bekanntermaßen verwendet, weil sie eine hohe Genauigkeit bieten, während sie sehr wenig Rechenleistung in Anspruch nehmen. SVMs können auch für Regressionsprobleme verwendet werden.

aus sklearn.svm importieren SVC

model = SVC( Kernel = 'linear' )

model.fit( X_train, y_train )

plot_mushroom_boundary( X_test, y_test, Modell)

Kasse: Python-Projekte auf GitHub

5. Naive Bayes

Wie der Name schon sagt, ist der Naive-Bayes-Algorithmus ein überwachter Lernalgorithmus, der auf dem Bayes-Theorem basiert . Das Bayes-Theorem verwendet bedingte Wahrscheinlichkeiten, um Ihnen die Wahrscheinlichkeit eines Ereignisses basierend auf einem bestimmten Wissen zu geben.

Woher,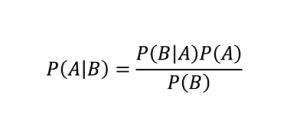

P (A | B): Die bedingte Wahrscheinlichkeit, dass Ereignis A eintritt, vorausgesetzt, dass Ereignis B bereits eingetreten ist. (Auch Posterior-Wahrscheinlichkeit genannt)

P(A): Wahrscheinlichkeit von Ereignis A.

P(B): Wahrscheinlichkeit von Ereignis B.

P (B | A): Die bedingte Wahrscheinlichkeit, dass Ereignis B eintritt, vorausgesetzt, dass Ereignis A bereits eingetreten ist.

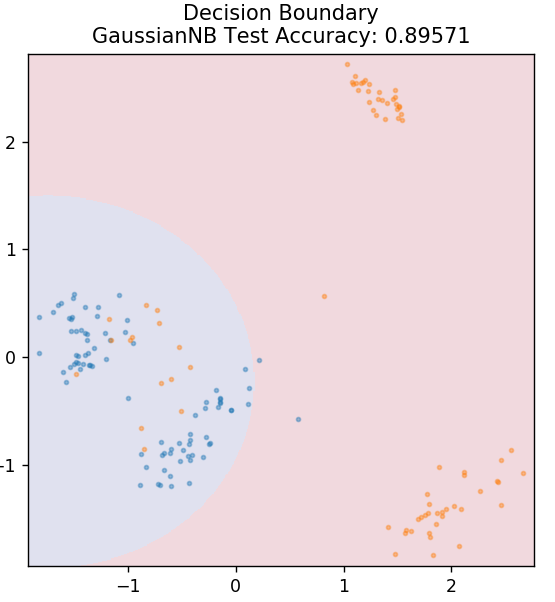
Warum heißt dieser Algorithmus Naive, fragen Sie? Dies liegt daran, dass davon ausgegangen wird, dass alle Vorkommnisse von Ereignissen unabhängig voneinander sind. Jedes Feature definiert also separat die Klasse, zu der ein Datenpunkt gehört, ohne Abhängigkeiten untereinander zu haben. Naive Bayes ist die beste Wahl für Textkategorisierungen. Es funktioniert auch mit kleinen Mengen an Trainingsdaten ausreichend gut.

aus sklearn.naive_bayes import GaussianNB

Modell = GaussianNB ()

model.fit( X_train, y_train )

plot_mushroom_boundary( X_test, y_test, Modell)

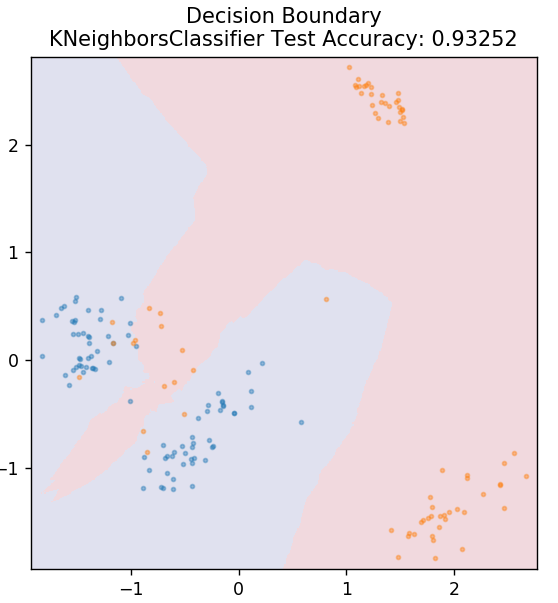
5. KN

KNN steht für K-nächste Nachbarn. Es ist ein sehr weit verbreiteter überwachter Lernalgorithmus, der die Testdaten nach Ähnlichkeiten mit den zuvor klassifizierten Trainingsdaten klassifiziert. KNN klassifiziert nicht alle Datenpunkte während des Trainings. Stattdessen speichert es nur den Datensatz und wenn es neue Daten erhält, klassifiziert es diese Datenpunkte basierend auf ihren Ähnlichkeiten. Dazu wird der euklidische Abstand der Zahl K der nächsten Nachbarn (hier n_neighbors ) dieses Datenpunkts berechnet.

aus sklearn.neighbors import KNeighborsClassifier

model = KNeighborsClassifier( n_neighbors = 20 )

model.fit( X_train, y_train )

plot_mushroom_boundary( X_test, y_test, Modell)

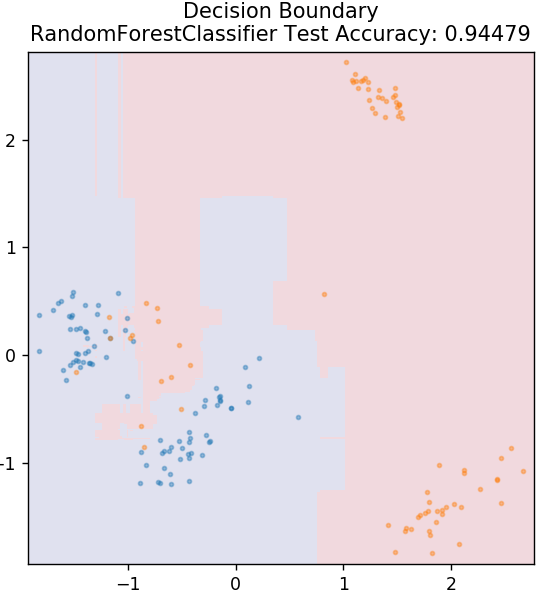
6. Zufälliger Wald

Random Forest ist ein sehr einfacher und vielfältiger Algorithmus für maschinelles Lernen, der eine Technik des überwachten Lernens verwendet. Wie der Name schon erahnen lässt, besteht Random Forest aus einer großen Anzahl von Entscheidungsbäumen, die als Ensemble agieren. Jeder Entscheidungsbaum ermittelt die Ausgabeklasse der Datenpunkte, und die Mehrheitsklasse wird als endgültige Ausgabe des Modells ausgewählt. Die Idee dabei ist, dass mehr Bäume, die an denselben Daten arbeiten, tendenziell genauere Ergebnisse liefern als einzelne Bäume.

aus sklearn.ensemble import RandomForestClassifier

model = RandomForestClassifier()

model.fit( X_train, y_train )

plot_mushroom_boundary( X_test, y_test, Modell)

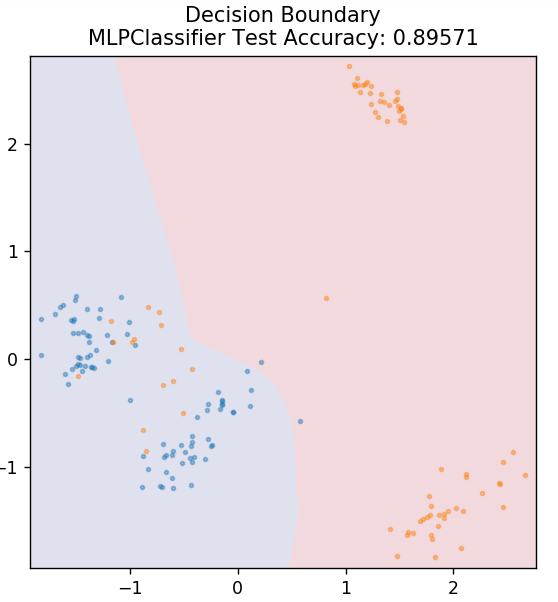
7. Mehrschichtiges Perzeptron

Multi-Layer Perceptron (oder MLP) ist ein sehr faszinierender Algorithmus, der in den Zweig des Deep Learning fällt. Genauer gesagt gehört es zur Klasse der Feed-Forward Artificial Neural Networks (ANN). MLP bildet ein Netzwerk aus mehreren Perzeptronen mit mindestens drei Schichten: einer Eingabeschicht, einer Ausgabeschicht und einer oder mehreren verborgenen Schichten. MLPs sind in der Lage, zwischen Daten zu unterscheiden, die nicht linear trennbar sind.

Jedes Neuron in den verborgenen Schichten verwendet eine Aktivierungsfunktion, um zur nächsten Schicht zu gelangen. Hier wird der Backpropagation-Algorithmus verwendet, um die Parameter tatsächlich abzustimmen und somit das neuronale Netzwerk zu trainieren. Es kann hauptsächlich für einfache Regressionsprobleme verwendet werden.

aus sklearn.neural_network MLPClassifier importieren

model = MLPClassifier()

model.fit( X_train, y_train )

plot_mushroom_boundary( X_test, y_test, Modell)

Lesen Sie auch: Ideen und Themen für Python-Projekte

Fazit

Wir können daraus schließen, dass unterschiedliche Algorithmen für maschinelles Lernen unterschiedliche Entscheidungsgrenzen und damit unterschiedliche Genauigkeitsergebnisse bei der Klassifizierung desselben Datensatzes ergeben.

Es gibt keine Möglichkeit, irgendeinen Algorithmus zum besten Algorithmus für alle Arten von Daten im Allgemeinen zu erklären. Maschinelles Lernen erfordert rigorose Versuche und Irrtümer für verschiedene Algorithmen, um festzustellen, was für jeden Datensatz separat am besten funktioniert. Die Liste der ML-Algorithmen endet hier offensichtlich nicht. Es gibt ein riesiges Meer anderer Techniken, die darauf warten, in der Scikit-Learn-Bibliothek von Python erkundet zu werden. Gehen Sie voran und trainieren Sie Ihre Datensätze mit all diesen und haben Sie Spaß!

Wenn Sie mehr über Entscheidungsbäume und maschinelles Lernen erfahren möchten, sehen Sie sich das Executive PG-Programm von IIIT-B & upGrad für maschinelles Lernen und KI an, das für Berufstätige konzipiert ist und mehr als 450 Stunden strenge Schulungen, mehr als 30 Fallstudien und Aufgaben, IIIT-B-Alumni-Status, mehr als 5 praktische praktische Abschlussprojekte und Arbeitsunterstützung bei Top-Unternehmen.