25 Interviewfragen und Antworten zum maschinellen Lernen – Lineare Regression
Veröffentlicht: 2022-09-08Es ist gängige Praxis, Data-Science-Anwärter in Interviews auf häufig verwendete Algorithmen für maschinelles Lernen zu testen. Diese herkömmlichen Algorithmen sind lineare Regression, logistische Regression, Clustering, Entscheidungsbäume usw. Von Datenwissenschaftlern wird erwartet, dass sie über fundierte Kenntnisse dieser Algorithmen verfügen.
Wir haben Personalchefs und Datenwissenschaftler aus verschiedenen Organisationen zu den typischen ML-Fragen befragt, die sie in einem Vorstellungsgespräch stellen. Basierend auf ihrem umfangreichen Feedback wurde eine Reihe von Fragen und Antworten vorbereitet, um angehenden Datenwissenschaftlern bei ihren Gesprächen zu helfen. Interviewfragen zur linearen Regression sind die häufigsten in Machine Learning-Interviews. Fragen und Antworten zu diesen Algorithmen werden in einer Reihe von vier Blogbeiträgen bereitgestellt.
Beste Online-Kurse für maschinelles Lernen und KI-Kurse
| Master of Science in Machine Learning & AI von der LJMU | Executive Post Graduate Program in Machine Learning & AI vom IIITB | |
| Advanced Certificate Program in Machine Learning & NLP von IIITB | Advanced Certificate Program in Machine Learning & Deep Learning von IIITB | Executive Post Graduate Program in Data Science & Machine Learning von der University of Maryland |
| Um alle unsere Kurse zu erkunden, besuchen Sie unsere Seite unten. | ||
| Kurse zum maschinellen Lernen | ||
Jeder Blog-Beitrag behandelt das folgende Thema:-
- Lineare Regression
- Logistische Regression
- Clustering
- Entscheidungsbäume und Fragen, die sich auf alle Algorithmen beziehen
Beginnen wir mit der linearen Regression!
1. Was ist lineare Regression?
Einfach ausgedrückt ist die lineare Regression eine Methode zum Finden der besten geraden Anpassung an die gegebenen Daten, dh zum Finden der besten linearen Beziehung zwischen den unabhängigen und abhängigen Variablen.
Technisch gesehen ist die lineare Regression ein maschineller Lernalgorithmus, der die beste lineare Anpassungsbeziehung für beliebige Daten zwischen unabhängigen und abhängigen Variablen findet. Dies geschieht meistens nach der Methode der Summe der quadratischen Residuen.
Gefragte maschinelle Lernfähigkeiten
| Kurse zu Künstlicher Intelligenz | Tableau-Kurse |
| NLP-Kurse | Deep-Learning-Kurse |

2. Geben Sie die Annahmen in einem linearen Regressionsmodell an.
Es gibt drei Hauptannahmen in einem linearen Regressionsmodell:
- Die Annahme über die Form des Modells:
Es wird angenommen, dass zwischen den abhängigen und unabhängigen Variablen ein linearer Zusammenhang besteht. Dies ist als „Linearitätsannahme“ bekannt. - Annahmen zu den Residuen:
- Normalitätsannahme: Es wird angenommen, dass die Fehlerterme ε (i) normalverteilt sind.
- Null-Mittelwert-Annahme: Es wird angenommen, dass die Residuen einen Mittelwert von Null haben.
- Annahme konstanter Varianz: Es wird angenommen, dass die Residualterme dieselbe (aber unbekannte) Varianz σ 2 haben. Diese Annahme ist auch als Annahme der Homogenität oder Homoskedastizität bekannt.
- Unabhängige Fehlerannahme: Es wird angenommen, dass die Restterme unabhängig voneinander sind, dh ihre paarweise Kovarianz ist Null.
- Annahmen zu den Schätzern:
- Die unabhängigen Variablen werden fehlerfrei gemessen.
- Die unabhängigen Variablen sind linear unabhängig voneinander, dh es gibt keine Multikollinearität in den Daten.
Erläuterung:
- Dies ist selbsterklärend.
- Wenn die Residuen nicht normalverteilt sind, geht ihre Zufälligkeit verloren, was bedeutet, dass das Modell die Beziehung in den Daten nicht erklären kann.
Außerdem sollte der Mittelwert der Residuen Null sein.
Y (i)i = β 0 + β 1 x (i) + ε (i)
Dies ist das angenommene lineare Modell, wobei ε der Restterm ist.
E(Y) = E( β 0 + β 1 x (i) + ε (i) )
= E( β 0 + β 1 x (i) + ε (i) )
Wenn die Erwartung (Mittelwert) der Residuen E(ε (i) ) Null ist, werden die Erwartungen der Zielvariablen und des Modells gleich, was eines der Ziele des Modells ist.
Die Residuen (auch bekannt als Fehlerterme) sollten unabhängig sein. Das bedeutet, dass es keine Korrelation zwischen den Residuen und den vorhergesagten Werten oder zwischen den Residuen selbst gibt. Wenn eine Korrelation vorhanden ist, impliziert dies, dass es eine Beziehung gibt, die das Regressionsmodell nicht identifizieren kann. - Wenn die unabhängigen Variablen nicht linear unabhängig voneinander sind, geht die Eindeutigkeit der Kleinste-Quadrate-Lösung (oder Normalgleichungslösung) verloren.
Nehmen Sie online am Kurs für künstliche Intelligenz von den besten Universitäten der Welt teil – Master, Executive Post Graduate Programs und Advanced Certificate Program in ML & AI, um Ihre Karriere zu beschleunigen.
3. Was ist Feature-Engineering? Wie wenden Sie es im Modellierungsprozess an?
Feature Engineering ist der Prozess der Umwandlung von Rohdaten in Features, die das zugrunde liegende Problem für die Vorhersagemodelle besser darstellen
, was zu einer verbesserten Modellgenauigkeit bei unsichtbaren Daten führt.
Laienhaft bedeutet Feature Engineering die Entwicklung neuer Features, die Ihnen helfen können, das Problem besser zu verstehen und zu modellieren. Es gibt zwei Arten von Feature-Engineering – geschäftsgesteuert und datengesteuert. Geschäftsorientiertes Feature-Engineering dreht sich um die Einbeziehung von Funktionen aus geschäftlicher Sicht. Die Aufgabe hier besteht darin, die Geschäftsvariablen in Merkmale des Problems umzuwandeln. Beim datengesteuerten Feature-Engineering haben die von Ihnen hinzugefügten Features keine signifikante physikalische Interpretation, aber sie helfen dem Modell bei der Vorhersage der Zielvariablen.
FYI: Kostenloser NLP-Kurs!
Um Feature Engineering anzuwenden, muss man mit dem Datensatz vollständig vertraut sein. Dazu gehört, zu wissen, was die gegebenen Daten sind, was sie bedeuten, was die Rohmerkmale sind usw. Sie müssen auch eine kristallklare Vorstellung von dem Problem haben, z. B. welche Faktoren die Zielvariable beeinflussen, wie die physikalische Interpretation der Variablen lautet , etc.
4. Was nützt die Regularisierung? Erklären Sie L1- und L2-Regularisierungen.
Regularisierung ist eine Technik, die verwendet wird, um das Problem der Überanpassung des Modells anzugehen. Wenn ein sehr komplexes Modell auf den Trainingsdaten implementiert wird, kommt es zu einer Überanpassung. Manchmal ist das einfache Modell möglicherweise nicht in der Lage, die Daten zu verallgemeinern, und das komplexe Modell überpasst. Um dieses Problem anzugehen, wird Regularisierung verwendet.
Regularisierung ist nichts anderes als das Hinzufügen der Koeffiziententerme (Betas) zur Kostenfunktion, so dass die Terme bestraft werden und eine kleine Größe haben. Dies hilft im Wesentlichen dabei, die Trends in den Daten zu erfassen und gleichzeitig eine Überanpassung zu verhindern, indem das Modell nicht zu komplex wird.
- L1- oder LASSO-Regularisierung: Hier werden die Absolutwerte der Koeffizienten zur Kostenfunktion addiert. Dies ist in der folgenden Gleichung ersichtlich; der hervorgehobene Teil entspricht der L1- oder LASSO-Regularisierung. Diese Regularisierungstechnik liefert spärliche Ergebnisse, die ebenfalls zu einer Merkmalsauswahl führen.
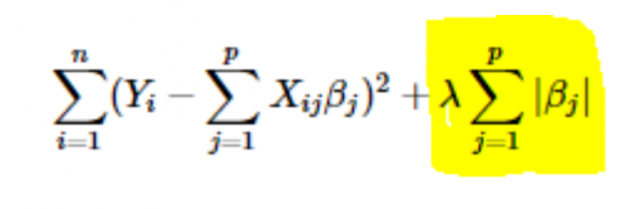
- L2- oder Ridge-Regularisierung: Hier werden die Quadrate der Koeffizienten zur Kostenfunktion addiert. Dies ist in der folgenden Gleichung zu sehen, wobei der hervorgehobene Teil der L2- oder Ridge-Regularisierung entspricht.
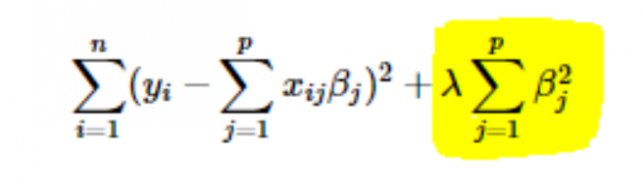
5. Wie wählt man den Wert des Parameters Lernrate (α)?
Die Auswahl des Wertes der Lernrate ist eine knifflige Angelegenheit. Wenn der Wert zu klein ist, dauert es ewig, bis der Gradientenabstiegsalgorithmus zur optimalen Lösung konvergiert. Wenn andererseits der Wert der Lernrate hoch ist, schießt der Gradientenabfall über die optimale Lösung hinaus und konvergiert höchstwahrscheinlich nie zur optimalen Lösung.
Um dieses Problem zu lösen, können Sie verschiedene Alpha-Werte über einen Wertebereich hinweg ausprobieren und die Kosten gegen die Anzahl der Iterationen darstellen. Dann kann basierend auf den Graphen der Wert ausgewählt werden, der dem Graphen entspricht, der die schnelle Abnahme zeigt. 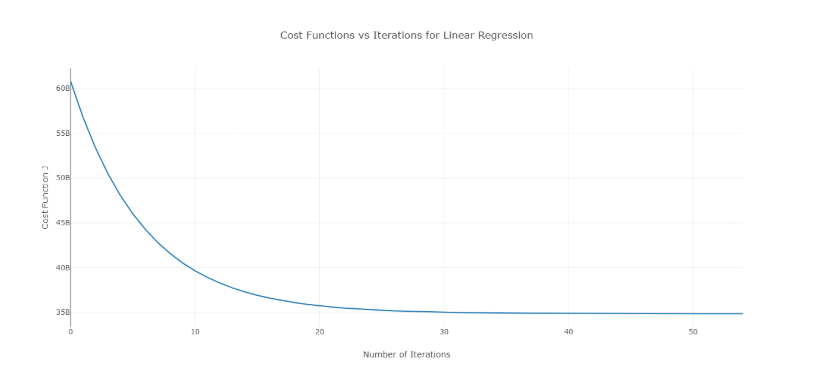
Das oben erwähnte Diagramm ist eine ideale Kosten-gegen-Anzahl-der-Iterations-Kurve. Beachten Sie, dass die Kosten anfänglich mit zunehmender Anzahl von Iterationen sinken, aber nach bestimmten Iterationen konvergiert der Gradientenabfall und die Kosten sinken nicht mehr.
Wenn Sie feststellen, dass die Kosten mit der Anzahl der Iterationen steigen, ist Ihr Lernratenparameter hoch und muss verringert werden.
6. Wie wählt man den Wert des Regularisierungsparameters (λ)?
Die Auswahl des Regularisierungsparameters ist eine knifflige Angelegenheit. Wenn der Wert von λ zu hoch ist, führt dies zu extrem kleinen Werten des Regressionskoeffizienten β , was zu einer Unteranpassung des Modells führt (hohe Verzerrung – niedrige Varianz). Wenn andererseits der Wert von λ 0 (sehr klein) ist, neigt das Modell dazu, die Trainingsdaten zu stark anzupassen (geringe Verzerrung – hohe Varianz).
Es gibt keinen geeigneten Weg, den Wert von λ auszuwählen . Was Sie tun können, ist, eine Unterstichprobe von Daten zu haben und den Algorithmus mehrmals auf verschiedenen Sätzen auszuführen. Hier muss die Person entscheiden, wie viel Varianz toleriert werden kann. Sobald der Benutzer mit der Varianz zufrieden ist, kann dieser Wert von λ für den vollständigen Datensatz gewählt werden.
Zu beachten ist, dass der hier ausgewählte Wert von λ für diese Teilmenge optimal war, nicht für die gesamten Trainingsdaten.
7. Können wir die lineare Regression für die Zeitreihenanalyse verwenden?
Man kann die lineare Regression für die Zeitreihenanalyse verwenden, aber die Ergebnisse sind nicht vielversprechend. Daher ist es generell nicht ratsam, dies zu tun. Die Gründe dafür sind –
- Zeitreihendaten werden hauptsächlich für die Vorhersage der Zukunft verwendet, aber die lineare Regression liefert selten gute Ergebnisse für die Vorhersage der Zukunft, da sie nicht für die Extrapolation gedacht ist.
- Meistens weisen Zeitreihendaten ein Muster auf, z. B. während der Hauptverkehrszeiten, Feiertage usw., das höchstwahrscheinlich als Ausreißer in der linearen Regressionsanalyse behandelt würde.
8. Welchem Wert liegt die Summe der Residuen einer linearen Regression nahe? Rechtfertigen.
Ans Die Summe der Residuen einer linearen Regression ist 0. Die lineare Regression geht davon aus, dass die Fehler (Residuen) normalverteilt mit einem Mittelwert von 0 sind, d. h
Y = β TX + ε
Hier ist Y die Ziel- oder abhängige Variable,
β ist der Vektor des Regressionskoeffizienten,
X ist die Merkmalsmatrix, die alle Merkmale als Spalten enthält,
ε ist der Restterm, so dass ε ~ N(0,σ 2 ).
Die Summe aller Residuen ist also der Erwartungswert der Residuen multipliziert mit der Gesamtzahl der Datenpunkte. Da der Erwartungswert der Residuen 0 ist, ist die Summe aller Residualterme null.
Hinweis : N(μ,σ 2 ) ist die Standardnotation für eine Normalverteilung mit Mittelwert μ und Standardabweichung σ 2 .
9. Wie wirkt sich Multikollinearität auf die lineare Regression aus?
Ans Multikollinearität tritt auf, wenn einige der unabhängigen Variablen stark (positiv oder negativ) miteinander korrelieren. Diese Multikollinearität verursacht ein Problem, da sie der Grundannahme einer linearen Regression widerspricht. Das Vorhandensein von Multikollinearität hat keinen Einfluss auf die Vorhersagefähigkeit des Modells. Wenn Sie also nur Vorhersagen wünschen, wirkt sich das Vorhandensein von Multikollinearität nicht auf Ihre Ausgabe aus. Wenn Sie jedoch einige Erkenntnisse aus dem Modell ziehen und diese beispielsweise in einem Geschäftsmodell anwenden möchten, kann dies zu Problemen führen.
Eines der Hauptprobleme, das durch Multikollinearität verursacht wird, besteht darin, dass sie zu falschen Interpretationen führt und falsche Erkenntnisse liefert. Die Koeffizienten der linearen Regression geben die mittlere Änderung des Zielwerts an, wenn ein Merkmal um eine Einheit geändert wird. Wenn also Multikollinearität besteht, gilt dies nicht, da die Änderung eines Merkmals zu Änderungen in der korrelierten Variablen und daraus resultierenden Änderungen in der Zielvariablen führt. Dies führt zu falschen Erkenntnissen und kann zu gefährlichen Ergebnissen für ein Unternehmen führen.
Eine sehr effektive Möglichkeit, mit Multikollinearität umzugehen, ist die Verwendung von VIF (Variance Inflation Factor). Je höher der Wert von VIF für ein Merkmal ist, desto linearer korreliert ist dieses Merkmal. Entfernen Sie einfach das Feature mit sehr hohem VIF-Wert und trainieren Sie das Modell erneut mit dem verbleibenden Datensatz.
10. Was ist die Normalform (Gleichung) der linearen Regression? Wann ist es der Gradientenabstiegsmethode vorzuziehen?
Die normale Gleichung für die lineare Regression ist —
β = (X T X) –1 . X T Y
Dabei ist Y=β T X das Modell für die lineare Regression,
Y ist die Ziel- oder abhängige Variable,
β ist der Vektor des Regressionskoeffizienten, der mit der Normalgleichung ermittelt wird,
X ist die Merkmalsmatrix, die alle Merkmale als Spalten enthält.
Beachten Sie hier, dass die erste Spalte in der X -Matrix nur aus Einsen besteht. Dies dient dazu, den Offset-Wert für die Regressionslinie einzubeziehen.
Vergleich zwischen Gradientenabstieg und Normalgleichung:
| Gradientenabstieg | Normale Gleichung |
| Benötigt Hyperparameter-Tuning für Alpha (Lernparameter) | Keine solche Notwendigkeit |
| Es ist ein iterativer Prozess | Es ist ein nicht iterativer Prozess |
| O(kn 2 ) Zeitkomplexität | O(n 3 ) Zeitkomplexität aufgrund der Auswertung von X T X |
| Bevorzugt, wenn n extrem groß ist | Wird für große Werte von n ziemlich langsam |
Hier ist „ k “ die maximale Anzahl von Iterationen für den Gradientenabstieg, und „ n “ ist die Gesamtzahl von Datenpunkten im Trainingssatz.
Wenn wir große Trainingsdaten haben, wird die normale Gleichung natürlich nicht zur Verwendung bevorzugt. Für kleine Werte von ' n ' ist die normale Gleichung schneller als der Gradientenabstieg.
Was ist maschinelles Lernen und warum ist es wichtig?
11. Sie führen Ihre Regression auf verschiedenen Teilmengen Ihrer Daten durch, und in jeder Teilmenge variiert der Beta-Wert für eine bestimmte Variable stark. Was könnte hier das Problem sein?
Dieser Fall impliziert, dass der Datensatz heterogen ist. Um dieses Problem zu lösen, sollte der Datensatz also in verschiedene Teilmengen geclustert werden, und dann sollten separate Modelle für jeden Cluster erstellt werden. Eine andere Möglichkeit, mit diesem Problem umzugehen, besteht darin, nichtparametrische Modelle wie Entscheidungsbäume zu verwenden, die recht effizient mit heterogenen Daten umgehen können.

12. Ihre lineare Regression läuft nicht und gibt an, dass es unendlich viele beste Schätzwerte für die Regressionskoeffizienten gibt. Was könnte falsch sein?
Diese Bedingung tritt auf, wenn zwischen einigen Variablen eine perfekte Korrelation (positiv oder negativ) besteht. In diesem Fall gibt es keinen eindeutigen Wert für die Koeffizienten, und daher ergibt sich die gegebene Bedingung.
13. Was meinen Sie mit angepasstem R 2 ? Wie unterscheidet es sich von R 2 ?
Das angepasste R 2 ist ebenso wie R 2 ein Repräsentant der Anzahl von Punkten, die um die Regressionslinie herum liegen. Das heißt, es zeigt, wie gut das Modell an die Trainingsdaten angepasst ist. Die Formel für angepasstes R 2 ist -
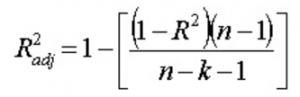
Hier ist n die Anzahl der Datenpunkte und k die Anzahl der Merkmale.
Ein Nachteil von R 2 ist, dass es mit dem Hinzufügen einer neuen Funktion immer größer wird, unabhängig davon, ob die neue Funktion nützlich ist oder nicht. Das angepasste R 2 überwindet diesen Nachteil. Der Wert des angepassten R 2 erhöht sich nur, wenn das neu hinzugefügte Merkmal eine signifikante Rolle im Modell spielt.
14. Wie interpretieren Sie die Residuen- vs. angepasste Wertkurve?
Das Diagramm Residuen vs. angepasster Wert wird verwendet, um zu sehen, ob die vorhergesagten Werte und Residuen eine Korrelation aufweisen oder nicht. Wenn die Residuen normal verteilt sind, mit einem Mittelwert um den angepassten Wert und einer konstanten Varianz, funktioniert unser Modell gut; Andernfalls liegt ein Problem mit dem Modell vor.
Das häufigste Problem, das beim Trainieren des Modells über einen großen Bereich eines Datensatzes gefunden werden kann, ist Heteroskedastizität (dies wird in der Antwort unten erklärt). Das Vorhandensein von Heteroskedastizität lässt sich leicht erkennen, indem man die Residuen-gegen-angepasste-Wert-Kurve grafisch darstellt.
15. Was ist Heteroskedastizität? Was sind die Folgen und wie kann man sie überwinden?
Eine Zufallsvariable wird als heteroskedastisch bezeichnet, wenn verschiedene Teilpopulationen unterschiedliche Variabilitäten (Standardabweichung) aufweisen.
Das Vorhandensein von Heteroskedastizität führt zu bestimmten Problemen bei der Regressionsanalyse, da die Annahme besagt, dass Fehlerterme nicht korreliert sind und daher die Varianz konstant ist. Das Vorhandensein von Heteroskedastizität kann oft in Form eines kegelförmigen Streudiagramms für Residuen vs. angepasste Werte gesehen werden.
Eine der Grundannahmen der linearen Regression ist, dass die Daten keine Heteroskedastizität aufweisen. Aufgrund der Verletzung von Annahmen sind die Ordinary Least Squares (OLS)-Schätzer nicht die Best Linear Unbiased Estimators (BLUE). Daher geben sie nicht die geringste Varianz als andere Linear Unbiased Estimators (LUEs).
Es gibt kein festgelegtes Verfahren zur Überwindung der Heteroskedastizität. Es gibt jedoch einige Möglichkeiten, die zu einer Verringerung der Heteroskedastizität führen können. Sie sind -
- Logarithmieren der Daten: Eine Reihe, die exponentiell ansteigt, führt oft zu einer erhöhten Variabilität. Dies kann mit der Log-Transformation überwunden werden.
- Verwenden der gewichteten linearen Regression: Hier wird die OLS-Methode auf die gewichteten Werte von X und Y angewendet. Eine Möglichkeit besteht darin, Gewichte hinzuzufügen, die direkt mit der Größe der abhängigen Variablen zusammenhängen.
16. Was ist VIF? Wie berechnen Sie es?
Der Varianzinflationsfaktor (VIF) wird verwendet, um das Vorhandensein von Multikollinearität in einem Datensatz zu überprüfen. Es wird berechnet als—
Hier ist VIF j der Wert von VIF für die j -te Variable,
R j 2 ist der R 2 -Wert des Modells, wenn diese Variable gegen alle anderen unabhängigen Variablen regressiert wird.
Wenn der Wert von VIF für eine Variable hoch ist, impliziert dies, dass das R 2 Wert des entsprechenden Modells hoch ist, dh andere unabhängige Variablen können diese Variable erklären. Einfach ausgedrückt ist die Variable linear abhängig von einigen anderen Variablen.
17. Woher wissen Sie, dass die lineare Regression für beliebige Daten geeignet ist?
Um zu sehen, ob die lineare Regression für bestimmte Daten geeignet ist, kann ein Streudiagramm verwendet werden. Wenn die Beziehung linear aussieht, können wir uns für ein lineares Modell entscheiden. Aber wenn dies nicht der Fall ist, müssen wir einige Transformationen anwenden, um die Beziehung linear zu machen. Das Zeichnen der Streudiagramme ist im Falle einer einfachen oder univariaten linearen Regression einfach. Im Falle einer multivariaten linearen Regression können jedoch zweidimensionale paarweise Streudiagramme, rotierende Diagramme und dynamische Diagramme gezeichnet werden.
18. Wie werden Hypothesentests in der linearen Regression verwendet?
Hypothesentests können in linearer Regression für folgende Zwecke durchgeführt werden:
- Überprüfung, ob ein Prädiktor signifikant für die Vorhersage der Zielvariablen ist. Zwei gängige Methoden dafür sind —
- Durch die Verwendung von p-Werten:
Wenn der p-Wert einer Variablen größer als ein bestimmter Grenzwert ist (normalerweise 0,05), ist die Variable für die Vorhersage der Zielvariablen unbedeutend. - Durch Überprüfung der Werte des Regressionskoeffizienten:
Wenn der Wert des Regressionskoeffizienten, der einem Prädiktor entspricht, Null ist, ist diese Variable in der Vorhersage der Zielvariablen unbedeutend und hat keine lineare Beziehung zu ihr.
- Durch die Verwendung von p-Werten:
- Um zu überprüfen, ob die berechneten Regressionskoeffizienten gute Schätzer der tatsächlichen Koeffizienten sind.
19. Erklären Sie den Gradientenabstieg in Bezug auf die lineare Regression.
Der Gradientenabstieg ist ein Optimierungsalgorithmus. Bei der linearen Regression wird es verwendet, um die Kostenfunktion zu optimieren und die Werte der βs (Schätzer) zu finden, die dem optimierten Wert der Kostenfunktion entsprechen.
Der Gradientenabstieg funktioniert wie ein Ball, der einen Graphen hinunterrollt (wobei die Trägheit ignoriert wird). Die Kugel bewegt sich entlang der Richtung der größten Steigung und kommt auf der ebenen Fläche (Minima) zur Ruhe. 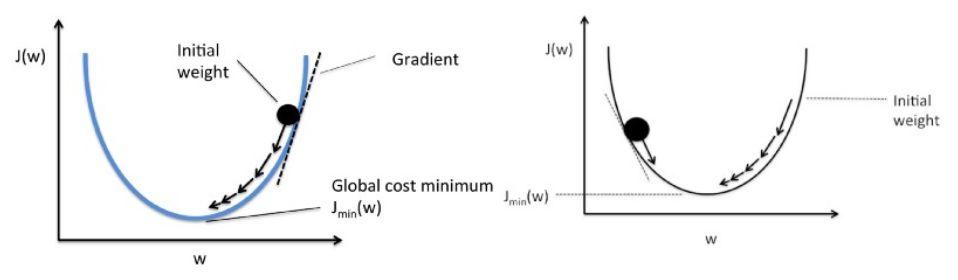
Mathematisch gesehen besteht das Ziel des Gradientenabstiegs für die lineare Regression darin, die Lösung von zu finden
ArgMin J(Θ 0 , Θ 1 ), wobei J(Θ 0 , Θ 1 ) die Kostenfunktion der linearen Regression ist. Es wird gegeben durch — 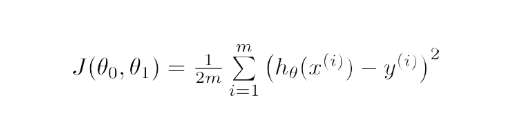
Dabei ist h das lineare Hypothesenmodell, h=Θ 0 + Θ 1 x, y ist die wahre Ausgabe und m ist die Anzahl der Datenpunkte im Trainingssatz.
Der Gradientenabstieg beginnt mit einer zufälligen Lösung, und dann wird die Lösung basierend auf der Richtung des Gradienten auf den neuen Wert aktualisiert, bei dem die Kostenfunktion einen niedrigeren Wert hat.
Die Aktualisierung ist:
Wiederholen bis zur Konvergenz 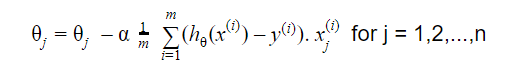
20. Wie interpretiert man ein lineares Regressionsmodell?
Ein lineares Regressionsmodell ist recht einfach zu interpretieren. Das Modell hat folgende Form: 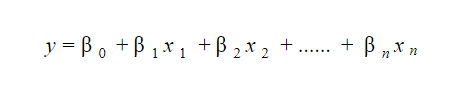
Die Bedeutung dieses Modells liegt darin, dass man die marginalen Veränderungen und ihre Folgen leicht interpretieren und nachvollziehen kann. Wenn beispielsweise der Wert von x 0 um 1 Einheit zunimmt, wobei andere Variablen konstant gehalten werden, ist die Gesamtzunahme des Werts von y β i . Mathematisch ist der Intercept-Term ( β 0 ) die Antwort, wenn alle Prädiktor-Terme auf Null gesetzt oder nicht berücksichtigt werden.
Diese 6 Techniken des maschinellen Lernens verbessern das Gesundheitswesen
21. Was ist robuste Regression?
Ein Regressionsmodell sollte robust sein. Das bedeutet, dass sich das Modell bei Änderungen in wenigen Beobachtungen nicht drastisch ändern sollte. Außerdem sollte es nicht stark von den Ausreißern beeinflusst werden.
Ein Regressionsmodell mit OLS (Ordinary Least Squares) reagiert recht empfindlich auf die Ausreißer. Um dieses Problem zu umgehen, können wir die WLS-Methode (Weighted Least Squares) verwenden, um die Schätzer der Regressionskoeffizienten zu bestimmen. Hier werden die Ausreißer oder Punkte mit hoher Hebelwirkung in der Anpassung weniger gewichtet, wodurch diese Punkte weniger wirkungsvoll sind.
22. Welche Graphen sollten vor der Modellanpassung beobachtet werden?
Vor dem Anpassen des Modells muss man sich der Daten bewusst sein, z. B. was die Trends, Verteilung, Schiefe usw. in den Variablen sind. Diagramme wie Histogramme, Boxplots und Dotplots können verwendet werden, um die Verteilung der Variablen zu beobachten. Abgesehen davon muss man auch analysieren, wie die Beziehung zwischen abhängigen und unabhängigen Variablen ist. Dies kann durch Streudiagramme (bei univariaten Problemen), rotierende Diagramme, dynamische Diagramme usw. erfolgen.
23. Was ist das verallgemeinerte lineare Modell?
Das verallgemeinerte lineare Modell ist die Ableitung des gewöhnlichen linearen Regressionsmodells. GLM ist in Bezug auf Residuen flexibler und kann verwendet werden, wenn eine lineare Regression nicht angemessen erscheint. GLM lässt zu, dass die Verteilung von Residuen anders als eine Normalverteilung ist. Es verallgemeinert die lineare Regression, indem es dem linearen Modell ermöglicht, mit der Verknüpfungsfunktion mit der Zielvariablen zu verknüpfen. Die Modellschätzung erfolgt nach der Methode der Maximum-Likelihood-Schätzung.
24. Erklären Sie den Bias-Varianz-Trade-off.
Bias bezieht sich auf die Differenz zwischen den vom Modell vorhergesagten Werten und den tatsächlichen Werten. Es ist ein Fehler. Eines der Ziele eines ML-Algorithmus ist es, eine geringe Verzerrung zu haben.
Varianz bezieht sich auf die Empfindlichkeit des Modells gegenüber kleinen Schwankungen im Trainingsdatensatz. Ein weiteres Ziel eines ML-Algorithmus ist eine geringe Varianz.
Bei einem nicht genau linearen Datensatz ist es nicht möglich, dass Bias und Varianz gleichzeitig niedrig sind. Ein lineares Modell hat eine geringe Varianz, aber eine hohe Abweichung, während ein Polynom hohen Grades eine geringe Abweichung, aber eine hohe Abweichung hat.
Beim maschinellen Lernen führt kein Weg an der Beziehung zwischen Verzerrung und Varianz vorbei.
- Eine Verringerung der Vorspannung erhöht die Varianz.
- Eine Verringerung der Varianz erhöht die Verzerrung.
Es gibt also einen Kompromiss zwischen den beiden; Der ML-Spezialist muss basierend auf dem zugewiesenen Problem entscheiden, wie viel Bias und Varianz toleriert werden können. Darauf aufbauend wird das endgültige Modell gebaut.
25. Wie können Lernkurven helfen, ein besseres Modell zu erstellen?
Lernkurven geben Aufschluss über das Vorhandensein von Overfitting oder Underfitting.
In einer Lernkurve werden der Trainingsfehler und der Kreuzvalidierungsfehler gegen die Anzahl der Trainingsdatenpunkte aufgetragen. Eine typische Lernkurve sieht so aus: 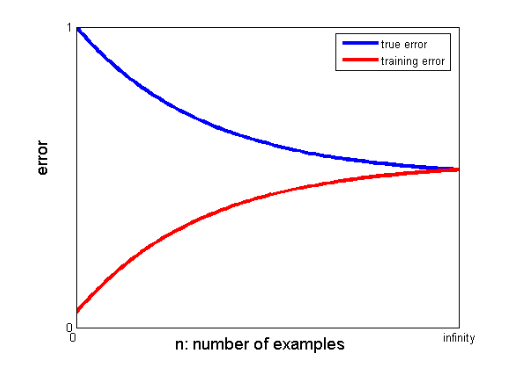
Wenn der Trainingsfehler und der wahre Fehler (Kreuzvalidierungsfehler) auf denselben Wert konvergieren und der entsprechende Wert des Fehlers hoch ist, weist dies darauf hin, dass das Modell unzureichend angepasst ist und unter einer hohen Verzerrung leidet.
Machine Learning Interviews und wie man sie meistert
Interviews mit maschinellem Lernen können je nach Art oder Kategorie variieren, z. B. stellen einige Personalvermittler viele Interviewfragen zur linearen Regression . Wenn sie sich für die Rolle des Machine Learning Engineer-Interviews entscheiden, können sie sich auf Kategorien wie Codierung, Forschung, Fallstudie, Projektmanagement, Präsentation, Systemdesign und Statistik spezialisieren. Wir konzentrieren uns auf die häufigsten Arten von Kategorien und darauf, wie man sich darauf vorbereitet.
- Kodierung
Kodierung und Programmierung sind wesentliche Bestandteile eines maschinellen Lerninterviews und werden häufig zum Screening von Bewerbern verwendet. Um in diesen Interviews gut abzuschneiden, müssen Sie über solide Programmierkenntnisse verfügen. Coding-Interviews dauern in der Regel 45 bis 60 Minuten und bestehen aus nur zwei Fragen. Der Interviewer stellt das Thema und geht davon aus, dass der Bewerber es so schnell wie möglich ansprechen wird.
So bereiten Sie sich vor – Sie können sich auf diese Interviews vorbereiten, indem Sie ein gutes Verständnis der Datenstrukturen, der zeitlichen und räumlichen Komplexität, Managementfähigkeiten und die Fähigkeit haben, ein Problem zu verstehen und zu lösen. upGrad hat einen großartigen Softwareentwicklungskurs, der Ihnen helfen kann, Ihre Programmierkenntnisse zu verbessern und das Vorstellungsgespräch zu meistern.
2. Maschinelles Lernen
Ihr Verständnis von maschinellem Lernen wird durch Interviews bewertet. Faltungsschichten, rekurrente neuronale Netze, generative gegnerische Netze, Spracherkennung und andere Themen können je nach Beschäftigungsbedarf behandelt werden.
So bereiten Sie sich vor – Um dieses Vorstellungsgespräch mit Bravour bestehen zu können, müssen Sie sicherstellen, dass Sie die Aufgaben und Verantwortlichkeiten der Stelle gründlich verstehen. Dies wird Ihnen helfen, die Spezifikationen von ML zu identifizieren, die Sie studieren müssen. Wenn Sie jedoch auf keine Spezifikationen stoßen, müssen Sie die Grundlagen gründlich verstehen. Ein Vertiefungskurs in ML, den upGrad anbietet, kann Ihnen dabei helfen. Sie können auch die neuesten Artikel zu ML und KI lesen, um ihre neuesten Trends zu verstehen, und Sie können sie regelmäßig einbeziehen.
3. Screening
Dieses Interview ist eher informell und in der Regel einer der Ausgangspunkte des Interviews. Ein potenzieller Arbeitgeber kümmert sich oft darum. Das Hauptziel dieses Gesprächs ist es, dem Bewerber einen Eindruck vom Unternehmen, der Rolle und den Aufgaben zu vermitteln. In einer informelleren Atmosphäre wird der Kandidat auch zu seiner Vergangenheit befragt, um festzustellen, ob sein Interessengebiet zur Position passt.
Vorbereitung – Dies ist ein sehr nicht-technischer Teil des Interviews. Alles, was Sie dafür brauchen, ist Ihre Ehrlichkeit und die Grundlagen Ihrer Spezialisierung auf Machine Learning.
4. Systemdesign
Solche Interviews testen die Fähigkeit einer Person, eine vollständig skalierbare Lösung von Anfang bis Ende zu erstellen. Die Mehrheit der Ingenieure ist so sehr mit einem Thema beschäftigt, dass sie häufig das Gesamtbild übersehen. Ein Systemdesign-Interview erfordert ein Verständnis zahlreicher Elemente, die zusammen eine Lösung ergeben. Zu diesen Elementen gehören das Front-End-Layout, der Load Balancer, der Cache und mehr. Ein effektives und skalierbares End-to-End-System ist einfacher zu entwickeln, wenn diese Probleme gut verstanden werden.
Vorbereitung – Verstehen Sie die Konzepte und Komponenten des Systemdesignprojekts. Verwenden Sie Beispiele aus der Praxis, um Ihrem Gesprächspartner die Struktur zu erklären, damit er das Projekt besser versteht.
Beliebte Blogs zu maschinellem Lernen und künstlicher Intelligenz
| IoT: Geschichte, Gegenwart und Zukunft | Lernprogramm für maschinelles Lernen: Lernen Sie ML | Was ist Algorithmus? Einfach & leicht |
| Gehalt als Robotikingenieur in Indien: Alle Rollen | Ein Tag im Leben eines Machine Learning Engineers: Was machen sie? | Was ist IoT (Internet der Dinge) |
| Permutation vs. Kombination: Unterschied zwischen Permutation und Kombination | Top 7 Trends in künstlicher Intelligenz und maschinellem Lernen | Maschinelles Lernen mit R: Alles, was Sie wissen müssen |

Wenn zwischen den konvergierenden Werten der Trainings- und Kreuzvalidierungsfehler eine signifikante Lücke besteht, dh der Kreuzvalidierungsfehler signifikant höher ist als der Trainingsfehler, deutet dies darauf hin, dass das Modell die Trainingsdaten überanpasst und unter einer hohen Varianz leidet .
Ingenieure für maschinelles Lernen: Mythen vs. Realitäten
Das ist das Ende des ersten Teils dieser Serie. Bleiben Sie dran für den nächsten Teil der Reihe, der aus Fragen besteht, die auf der logistischen Regression basieren . Fühlen Sie sich frei, Ihre Kommentare zu posten.
Co-Autor von – Ojas Agarwal
Sie können unser Executive PG-Programm für maschinelles Lernen und KI einsehen , das praktische Workshops, persönliche Mentoren aus der Industrie, 12 Fallstudien und Aufgaben, IIIT-B-Alumni-Status und mehr bietet.
Was verstehst du unter Regularisierung?
Regularisierung ist eine Strategie, um mit dem Problem der Modellüberanpassung umzugehen. Overfitting tritt auf, wenn ein kompliziertes Modell auf Trainingsdaten angewendet wird. Das Basismodell kann die Daten manchmal nicht verallgemeinern, und das komplizierte Modell kann die Daten überanpassen. Regularisierung wird verwendet, um dieses Problem zu lindern. Regularisierung ist der Vorgang des Hinzufügens von Koeffiziententermen (Betas) zum Minimierungsproblem in einer Weise, dass die Terme bestraft werden und eine bescheidene Größe haben. Dies hilft im Wesentlichen bei der Identifizierung von Datenmustern und verhindert gleichzeitig eine Überanpassung, indem verhindert wird, dass das Modell zu komplex wird.
Was verstehen Sie unter Feature Engineering?
Der Prozess der Umwandlung von Originaldaten in Features, die das zugrunde liegende Problem für Vorhersagemodelle besser beschreiben, was zu einer verbesserten Modellgenauigkeit bei unsichtbaren Daten führt, wird als Feature Engineering bezeichnet. Laienhaft ausgedrückt bezieht sich Feature Engineering auf die Erstellung zusätzlicher Features, die zum besseren Verständnis und Modellieren eines Problems beitragen können. Es gibt zwei Arten von Feature Engineering: geschäftsgesteuert und datengesteuert. Die Einbindung von Features aus kaufmännischer Sicht steht im Mittelpunkt des Business Driven Feature Engineering.
Was ist der Bias-Varianz-Tradeoff?
Die Lücke zwischen den vom Modell vorhergesagten Werten und den tatsächlichen Werten wird als Bias bezeichnet. Es ist ein Fehler. Eine geringe Verzerrung ist eines der Ziele eines ML-Algorithmus. Die Anfälligkeit des Modells gegenüber winzigen Änderungen im Trainingsdatensatz wird als Varianz bezeichnet. Niedrige Varianz ist ein weiteres Ziel eines ML-Algorithmus. Es ist unmöglich, sowohl eine geringe Verzerrung als auch eine geringe Varianz in einem Datensatz zu haben, der nicht perfekt linear ist. Die Varianz eines Modells mit geraden Linien ist gering, aber die systematische Abweichung ist groß, während die Varianz eines Polynoms hohen Grades gering, aber die systematische Abweichung hoch ist. Beim maschinellen Lernen ist die Verbindung zwischen Verzerrung und Variation unvermeidlich.
