Einführung in die Wahrscheinlichkeitsdichtefunktion [Formel, Eigenschaften, Anwendungen, Beispiele]

Die Wahrscheinlichkeitsdichtefunktion (PDF) ist ein Ausdruck in der Statistik, der die Wahrscheinlichkeitsverteilung einer diskreten Zufallsvariablen bezeichnet. Die Wahrscheinlichkeitsverteilung kann einfach ausgedrückt als die Wahrscheinlichkeit des Ergebnisses einer Zufallsvariablen wie einer Aktie oder eines ETF definiert werden. Diskrete Variablen treten im Gegensatz zu einer kontinuierlichen Zufallsvariablen auf, deren genauer Wert bestimmt werden kann.

Beispielsweise hat der Wert eines Scrips an einer Börse nur zwei Dezimalstellen (z. B. 65,76) in einer diskreten Zufallsvariablen anstelle einer kontinuierlichen Variablen mit einer beliebigen Anzahl von Dezimalstellen (Beispiel: 65,7685434567).

Eine Wahrscheinlichkeitsdichtefunktion ist ein statistisches Werkzeug, das verwendet wird, um die Wahrscheinlichkeit des Ergebnisses einer diskreten Zufallsvariablen zu bestimmen. In einem Diagramm dargestellt, sehen PDFs identisch mit einer Glockenkurve aus, bei der die Fläche unter der Kurve die Wahrscheinlichkeit des Ergebnisses darstellt.

Als grafisches Modell projiziert stellt die Fläche unter der Kurve den Bereich dar, in den die Werte der diskreten Zufallsvariablen fallen werden. Somit ist die Gesamtfläche unter der Kurve gleich der Wahrscheinlichkeit des Ergebnisses der Variablen.

Die Wahrscheinlichkeitsdichtefunktion kann die Wahrscheinlichkeit bestimmen, dass eine Zufallsvariable in einen bestimmten Wertebereich fällt.

Typischerweise analysieren Wahrscheinlichkeitsdichtefunktionen die Risiken und potenziellen Erträge, die mit einem bestimmten Fonds an der Börse verbunden sind.

Bedingungen, die eine Funktion erfüllen muss, um als Wahrscheinlichkeitsdichtefunktion betrachtet zu werden

Der Wert einer diskreten Variablen kann im Gegensatz zu einer kontinuierlichen Variablen, die unendlich viele Werte haben kann, genau gemessen werden. Jede Funktion sollte die folgenden zwei Bedingungen erfüllen, um eine Wahrscheinlichkeitsdichtefunktion zu sein:

• Der f(x)-Wert für jeden möglichen Wert der Zufallsvariablen sollte positiv (nicht negativ) sein.
• Der Integralwert der Gesamtfläche der Kurve (Integral aller möglichen Werte der Zufallsvariablen) soll 1 sein.

Unterschied zwischen Wahrscheinlichkeitsdichtefunktion und Wahrscheinlichkeitsverteilungsfunktion

Zufallsvariablen können viele Werte haben. Die Beschreibung aller möglichen Werte, die eine Zufallsvariable haben kann, wird als Wahrscheinlichkeitsverteilung bezeichnet.

Die Wahrscheinlichkeitsverteilung gibt eine Reihe von Ergebnissen und ihre zugehörigen Wahrscheinlichkeiten an. Die statistische Funktion, die eine kontinuierliche Wahrscheinlichkeitsverteilung darstellt, wird als Wahrscheinlichkeitsdichtefunktion bezeichnet.

Es gibt ein weiteres statistisches Werkzeug, das eine diskrete Wahrscheinlichkeitsverteilung darstellt, die als Wahrscheinlichkeitsmassenfunktion bezeichnet wird. Dies gibt einen detaillierten Überblick über alle möglichen Ergebnisse und ihre Wahrscheinlichkeitswahrscheinlichkeiten.

Ausdruck für Wahrscheinlichkeitsdichtefunktionen

Wenn die Zufallsvariable diskret ist, wird ihre Wahrscheinlichkeitsverteilung als Wahrscheinlichkeitsmassenfunktion bezeichnet, und wenn sie eine kontinuierliche Variable ist, wird die Wahrscheinlichkeitsverteilung als Wahrscheinlichkeitsdichtefunktion bezeichnet.

Ein PDF wird verwendet, wenn die betreffende Zufallsvariable einen Bereich möglicher Werte hat. Ihre Wahrscheinlichkeitsverteilung wird verwendet, um den genauen Wert zu bestimmen.

Die Zufallsvariable sei mit X bezeichnet. Die Wahrscheinlichkeitsdichtefunktion f der Zufallsvariablen X kann ausgedrückt werden als

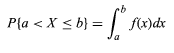
• Der Wert der Zufallsvariablen liegt zwischen a und b.
• Wenn X die Wahrscheinlichkeit bezeichnet, eine bestimmte Zahl aus dem Bereich (Intervall) r und s auszuwählen, dann kann die Wahrscheinlichkeitsdichtefunktion ausgedrückt werden als

f ( x ) = 1/( s − r ) für r < x < s und f ( x ) = 0 für x < r oder x > s .

• Das PDF F wird dargestellt als:

F ( x ) = P { X ≤ x }

die als Verteilungsfunktion oder kumulative Verteilungsfunktion von X bezeichnet wird.

Wenn man bedenkt, dass die Zufallsvariable X eine Wahrscheinlichkeitsverteilungsfunktion f ( x ) hat, dann kann die Beziehung zwischen f und F hergestellt werden als

F '(. x ) = f ( x )

Die Verteilungsfunktion einer diskreten Zufallsvariablen unterscheidet sich von ihrer Wahrscheinlichkeitsverteilungsfunktion. Die Beziehung zwischen den beiden kann wie folgt ausgedrückt werden:

Der Erwartungswert der Zufallsvariablen wird bezeichnet als

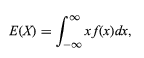
Somit können alle diskreten und zufälligen Variablen mit Hilfe einer kombinierten Theorie einheitlich behandelt werden.

Die Formel der Wahrscheinlichkeitsdichtefunktion

Die Wahrscheinlichkeit einer kontinuierlichen Zufallsvariablen X auf einem festen Wert x ist immer 0. In diesem Fall kann P(X = x) nicht verwendet werden. Der zwischen einem Wertebereich (a,b) liegende Wert von X soll ermittelt werden. Um dasselbe zu bestimmen, wird die folgende Formel verwendet.

Eigenschaften einer Wahrscheinlichkeitsdichtefunktion

Eine kontinuierliche Zufallsvariable, die beispielsweise ihren Wert zwischen dem Bereich (a, b) annimmt, wird geschätzt, indem die Fläche unter der Kurve und der X-Achse berechnet wird, die mit (a) als Untergrenze und (b) als Untergrenze aufgetragen ist Höchstgrenze. Die Wahrscheinlichkeitsdichtefunktion für das Obige wird dargestellt als:

Die Wahrscheinlichkeitsdichtefunktion ist für alle möglichen Werte positiv (nicht negativ). Das bedeutet f(x)≥ 0, für jedes x. Die Fläche, die zwischen die Dichtekurve und die X-Achse (horizontale Achse) fällt, ist gleich 1.

Dies kann auch bezeichnet werden als:

Die Kurve der Dichtefunktion ist über den gesamten angegebenen Bereich kontinuierlich, der klar gegen eine Reihe kontinuierlicher Werte oder den Definitionsbereich der Variablen definiert ist.

Nehmen Sie online am Machine Learning-Kurs der weltbesten Universitäten teil – Master, Executive Post Graduate Programs und Advanced Certificate Program in ML & AI, um Ihre Karriere zu beschleunigen.

Anwendungen der Wahrscheinlichkeitsdichtefunktion

• Die Wahrscheinlichkeitsdichtefunktion wird bei der jährlichen Modellierung atmosphärischer NO-Konzentrationsniveaus verwendet.
• Modellierung der dieselmotorischen Verbrennung.
• In der Statistik wird die Wahrscheinlichkeitsdichtefunktion verwendet, um die Möglichkeiten des Ergebnisses einer Zufallsvariablen zu bestimmen.

Beispiele für die Wahrscheinlichkeitsdichtefunktion

• Beispiel 1

Nachfolgend ein Beispiel, wie die Wahrscheinlichkeitsdichtefunktion (PDF) verwendet wird, um das Risikopotenzial eines Anlegers an der Börse zu bestimmen:

Zunächst werden PDFs als grafisches Hilfsmittel auf Basis historischer Informationen generiert.

Die häufigste Form von PDF ist die neutrale Projektion, bei der das Risiko bei einer Reihe von Möglichkeiten gleich der Belohnung ist. Anleger mit geringerer Risikobereitschaft werden nur mit begrenzten Gewinnen belohnt und fallen daher unter die linke Seite der Glockenkurve. Umgekehrt werden Anleger mit hoher Risikobereitschaft wahrscheinlich mit höheren Renditen belohnt und fallen daher auf die rechte Seite der Kurve.

Die meisten Anleger fallen unter die durchschnittliche Risikobereitschaft und befinden sich daher in der Mitte der Kurve.

Dies hilft bei der Analyse der Anlegerkategorie auf der Grundlage der erhaltenen Daten. Dies hilft Börsenmaklern, ihre Zielkundenkategorie für den Verkauf ihrer Produkte zu identifizieren.

• Beispiel 2

Eine der wesentlichen Anwendungen der Wahrscheinlichkeitsdichtefunktion ist die Gaußsche Zufallsvariable, auch bekannt als normale Zufallsvariable.

In beiden Fällen ergibt der Graph eine Glockenkurve für die Wahrscheinlichkeitsdichtefunktion.

Die Dichte kann ausgedrückt werden als

Der Graph der obigen Dichtegleichung ist unten angegeben.

Die Fläche unter der Kurve repräsentiert den tatsächlichen Wert der Gaußschen Zufallsvariablen.

Fazit

Die Wahrscheinlichkeitsdichtefunktion spielt eine wichtige Rolle beim maschinellen Lernen. Studenten, die eine Karriere in maschinellem Lernen und künstlicher Intelligenz anstreben, empfehlen wir dringend, sich für das IIT-Advanced Certificate Program in Machine Learning von upGrad anzumelden . Das Programm ist maßgeschneidert und darauf ausgelegt, hochrangige Berufstätige in die Lage zu versetzen, maschinelle Lernmodelle mithilfe von Cloud-Computing-Technologie einzusetzen.

Der Lehrplan wurde von der Fakultät des IIT Madras und Branchenexperten entwickelt, um den Lernprozess relevanter und praktischer zu gestalten. Das Programm bietet eine weltweit anerkannte Zertifizierung des begehrten und auf Platz 1 rangierenden Engineering College in Indien und eine 360-Grad-Vermittlungsunterstützung von upGrad.

Darüber hinaus erhalten Sie zahlreiche Möglichkeiten, an groß angelegten Projekten mit upGrads bezahlter Lernerbasis von über 40.000 zusammenzuarbeiten.

Besuchen Sie unsere Website, um Ihre Lernreise zu beginnen!