Einführung in die multivariate Regression beim maschinellen Lernen: Vollständiger Leitfaden

Es ist kein Geheimnis, dass die heutige Technologie datengesteuert ist. Daten sind zwar nur eine Zusammenstellung von Zahlen, können aber sinnvoll verarbeitet werden, um Produktivität und Einfallsreichtum für Unternehmen zu extrahieren, um langfristig wettbewerbsfähig und nachhaltig zu bleiben. Tatsächlich ist die Datenanalyse die Antwort darauf, genaue Schätzungen aus Rohinformationen abzuleiten.

Die Datenanalyse ist eine Technik, die statistische und logische Ideen beinhaltet, um Daten zu untersuchen, zu verarbeiten und in eine nutzbare Form umzuwandeln. Die Lösungen, die durch Datenanalyse gezogen werden, werden in Unternehmen verwendet, um wichtige Entscheidungen zu treffen. Data Science zusammen mit Datenanalyse wird verwendet, um zukünftige Ergebnisse mit hoher Genauigkeit vorherzusagen. Es ist ein Prozess, bei dem wissenschaftliche Techniken und Algorithmen eingesetzt werden, um brauchbare Informationen aus einem Datenpool zu gewinnen.

Ein häufiges Problem, mit dem Datenfachleute konfrontiert sind, ist die Art und Weise, wie festgestellt werden kann, ob eine statistische Beziehung zwischen einer Antwortvariablen (bezeichnet mit Y) und erklärenden Variablen (bezeichnet mit Xi) besteht.

Die Antwort auf diese Bedenken ist die Regressionsanalyse. Lassen Sie uns dies genauer verstehen.

Was ist Regressionsanalyse?

Die Regressionsanalyse ist eine der beliebtesten Methoden in der Datenanalyse, die einem kontrollierten oder überwachten maschinellen Lernalgorithmus folgt. Es ist eine effektive Technik, um eine Beziehung zwischen Variablen in Daten zu identifizieren und herzustellen.

Bei der Regressionsanalyse werden brauchbare Variablen mithilfe mathematischer Strategien aussortiert, um hochgenaue Schlussfolgerungen über diese sortierten Variablen zu ziehen.

Was ist multivariate Regression?

Multivariate ist ein kontrollierter oder überwachter maschineller Lernalgorithmus, der mehrere Datenvariablen analysiert. Es ist eine Fortsetzung der multiplen Regression, die eine abhängige Variable und viele unabhängige Variablen umfasst. Die Ausgabe wird basierend auf der Anzahl der unabhängigen Variablen vorhergesagt.

Die multivariate Regression ermittelt eine Formel, die die gleichzeitige Reaktion der in Variablen vorhandenen Faktoren auf die Änderungen in anderen erklärt. Sie werden verwendet, um die Daten in verschiedenen Bereichen zu untersuchen. Beispielsweise wird im Immobilienbereich die multivariate Regression verwendet, um den Preis eines Hauses basierend auf mehreren Faktoren wie Standort, Anzahl der Zimmer und verfügbaren Annehmlichkeiten vorherzusagen.

Kostenfunktion in der multivariaten Regression

Die Kostenfunktion ordnet Stichproben Kosten zu, wenn das Ergebnis eines Modells von den beobachteten Daten abweicht. Die Kostengleichungsfunktion ist die Summe des Quadrats der Differenz zwischen dem vorhergesagten Wert und dem tatsächlichen Wert dividiert durch die zweifache Länge des Datensatzes.

Hier ist ein Beispiel :

Ergebnis :

Quelle

Wie verwende ich die multivariate Regressionsanalyse?

Die an der multivariaten Regressionsanalyse beteiligten Prozesse umfassen die Auswahl von Merkmalen, das Konstruieren der Merkmale, die Merkmalsnormalisierung, Auswahlverlustfunktionen, Hypothesenanalyse und das Erstellen eines Regressionsmodells.

1. Auswahl von Merkmalen: Dies ist der wichtigste Schritt in der multivariaten Regression. Dieser Prozess, der auch als Variablenauswahl bezeichnet wird, umfasst die Auswahl geeigneter Variablen, um effiziente Modelle zu erstellen.
2. Merkmalsnormalisierung: Dies beinhaltet die Merkmalsskalierung, um eine optimierte Verteilung und Datenverhältnisse aufrechtzuerhalten. Dies hilft bei einer besseren Datenanalyse. Der Wert aller Merkmale kann je nach Anforderung geändert werden.
3. Verlustfunktion und -hypothese auswählen : Die Verlustfunktion wird zum Vorhersagen von Fehlern verwendet. Die Verlustfunktion kommt ins Spiel, wenn sich die Hypothesenvorhersage von den tatsächlichen Zahlen unterscheidet. Hier stellt die Hypothese den aus dem Merkmal oder der Variablen vorhergesagten Wert dar.
4. Fixing-Hypothesenparameter : Der Parameter der Hypothese wird fixiert oder so eingestellt, dass er die Verlustfunktion minimiert und eine bessere Vorhersage verbessert.
5. Reduzieren der Verlustfunktion : Die Verlustfunktion wird minimiert, indem ein Algorithmus speziell für die Verlustminimierung auf dem Datensatz erzeugt wird, was wiederum die Änderung von Hypotheseparametern erleichtert. Der Gradientenabstieg ist der am häufigsten verwendete Algorithmus zur Verlustminimierung. Der Algorithmus kann auch für andere Aktionen verwendet werden, sobald die Verlustminimierung abgeschlossen ist.
6. Analyse der Hypothesenfunktion : Die Funktion der Hypothese muss analysiert werden, da sie für die Vorhersage der Werte entscheidend ist. Nachdem die Funktion analysiert wurde, wird sie dann anhand von Testdaten getestet.

Betrachten wir nun die zwei Möglichkeiten, wie die multivariate Regression verwendet werden kann.

1. Multivariate lineare Regression

Die multivariate lineare Regression ähnelt der einfachen linearen Regression, außer dass bei der multivariaten linearen Regression mehrere unabhängige Variablen zu den abhängigen Variablen beitragen und daher mehrere Koeffizienten bei der Berechnung verwendet werden.

• Es wird verwendet, um eine mathematische Beziehung zwischen mehreren Zufallsvariablen abzuleiten. Es erklärt, wie viele mehrere unabhängige Variablen einer abhängigen Variablen zugeordnet sind.
• Die Details der mehreren unabhängigen Variablen werden verwendet, um eine genaue Vorhersage des Einflusses zu treffen, den sie auf die Ergebnisvariable haben.
• Das multivariate lineare Regressionsmodell generiert eine Beziehung in linearer Form (eine Form einer geraden Linie) mit der besten Annäherung an jeden Datenpunkt.
• Die Gleichung des multivariaten linearen Regressionsmodells lautet:

yi​=β0​+β1​xi1​+β2​xi2​+…+βp​xip​+

wobei für i=n Beobachtungen:

Quelle

Wann kann die lineare Regression verwendet werden?

Das lineare Regressionsmodell kann nur verwendet werden, wenn es zwei kontinuierliche Variablen gibt, von denen eine abhängig und die andere unabhängig ist.

Die unabhängige Variable wird als Parameter verwendet, um den Wert oder das Ergebnis der abhängigen Variablen zu bestimmen.

2. Multivariate logistische Regression

Die logistische Regression ist ein Algorithmus, der verwendet wird, um ein binäres Ergebnis basierend auf mehreren unabhängigen Variablen vorherzusagen. Ein binäres Ergebnis hat zwei Möglichkeiten, entweder das Szenario tritt ein (dargestellt durch 1) oder es tritt nicht ein (gekennzeichnet durch 0).

Die logistische Regression wird bei der Arbeit mit binären Daten verwendet, den Daten, bei denen das Ergebnis (oder die abhängige Variable) dichotom ist.

Wo kann die logistische Regression eingesetzt werden?

Die logistische Regression wird hauptsächlich zur Behandlung von Klassifizierungsproblemen verwendet. Zum Beispiel, um festzustellen, ob eine E-Mail Spam ist oder nicht und ob eine bestimmte Transaktion böswillig ist oder nicht. In der Datenanalyse wird es verwendet, um kalkulierte Entscheidungen zu treffen, um Verluste zu minimieren und Gewinne zu steigern.

Die multivariate logistische Regression wird verwendet, wenn es eine abhängige Variable und mehrere Ergebnisse gibt. Sie unterscheidet sich von der logistischen Regression dadurch, dass sie mehr als zwei mögliche Ergebnisse hat.

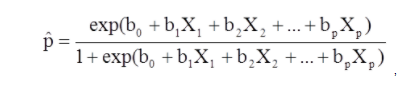
X1 bis Xp sind unterschiedliche unabhängige Variablen.

b0 bis bp sind die Regressionskoeffizienten

Das multiple logistische Regressionsmodell kann auch in anderer Form geschrieben werden. Im nachstehenden Formular ist das Ergebnis der erwartete Log der Quoten, dass das Ergebnis vorhanden ist,

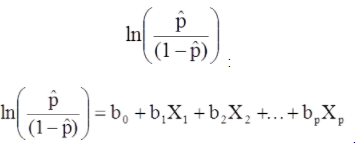
Das multiple logistische Regressionsmodell kann auch in anderer Form geschrieben werden. Im nachstehenden Formular ist das Ergebnis der erwartete Log der Quoten, dass das Ergebnis vorhanden ist.

Die rechte Seite der obigen Gleichung ähnelt der linearen Regressionsgleichung, aber die Methode zum Ermitteln der Regressionskoeffizienten unterscheidet sich.

Annahmen im multivariaten Regressionsmodell

• Die abhängige und die unabhängige Variable haben eine lineare Beziehung.
• Die unabhängigen Variablen haben untereinander keine starke Korrelation.
• Die Beobachtungen von yi werden zufällig und individuell aus der Bevölkerung ausgewählt.

Annahmen im multivariaten logistischen Regressionsmodell

• Die abhängige Variable ist nominal oder ordinal. Die nominalen Variablen haben zwei oder mehr Kategorien ohne sinnvolle Organisation. Ordinale Variablen können auch zwei oder mehr Kategorien haben, aber sie haben eine Struktur und können in eine Rangfolge gebracht werden.
• Es kann einzelne oder mehrere unabhängige Variablen geben, die ordinal, stetig oder nominal sein können. Kontinuierliche Variablen sind solche, die innerhalb eines bestimmten Bereichs unendliche Werte haben können.
• Die abhängigen Variablen schließen sich gegenseitig aus und sind erschöpfend.
• Die unabhängigen Variablen haben untereinander keine starke Korrelation.

Vorteile der multivariaten Regression

1. Die multivariate Regression hilft uns, die Beziehungen zwischen mehreren Variablen im Datensatz zu untersuchen.
2. Die Korrelation zwischen abhängigen und unabhängigen Variablen hilft bei der Vorhersage des Ergebnisses.
3. Es ist einer der bequemsten und beliebtesten Algorithmen, die beim maschinellen Lernen verwendet werden.

Nachteile der multivariaten Regression

• Die Komplexität multivariater Techniken erfordert komplexe mathematische Berechnungen.
• Es ist nicht einfach, die Ausgabe des multivariaten Regressionsmodells zu interpretieren, da es Inkonsistenzen in den Verlust- und Fehlerausgaben gibt.
• Multivariate Regressionsmodelle können nicht auf kleinere Datensätze angewendet werden; sie sind darauf ausgelegt, genaue Ausgaben zu erzeugen, wenn es um größere Datensätze geht.

Wenn Sie mehr über multivariate Regression und andere komplexe Data-Science-Themen erfahren möchten, hat upGrad genau die richtige Lösung für Sie. Unser 18-monatiger Master of Science in Data Science an der Liverpool John Moores University umfasst mehr als 500 strenge Lernstunden, 25 Coaching-Sitzungen (auf einer 1:8-Basis) und mehr als 20 Live-Sitzungen. upGrad bietet auch 1:1-Unterrichtsunterstützung und 360°-Berufsberatungsunterstützung für Studenten, um ihre Karriere zu verändern. Lernende können Peer-to-Peer-Lernen auf der globalen Plattform mit über 40.000 bezahlten Lernenden nutzen und an Gemeinschaftsprojekten in sechs funktionalen Spezialisierungen arbeiten, um ihre Lernerfahrung zu maximieren.