Gradientenabstieg beim maschinellen Lernen: Wie funktioniert es?

Einführung

Einer der wichtigsten Teile des maschinellen Lernens ist die Optimierung seiner Algorithmen. Fast alle Algorithmen im maschinellen Lernen haben einen Optimierungsalgorithmus an ihrer Basis, der als Kern des Algorithmus fungiert. Wie wir alle wissen, ist die Optimierung das ultimative Ziel jedes Algorithmus, selbst bei realen Ereignissen oder wenn es um ein technologiebasiertes Produkt auf dem Markt geht.

Derzeit gibt es viele Optimierungsalgorithmen, die in verschiedenen Anwendungen wie Gesichtserkennung, selbstfahrenden Autos, marktbasierten Analysen usw. verwendet werden. Auch beim maschinellen Lernen spielen solche Optimierungsalgorithmen eine wichtige Rolle. Ein solcher weit verbreiteter Optimierungsalgorithmus ist der Gradientenabstiegsalgorithmus, den wir in diesem Artikel durchgehen werden.

Was ist Gradient Descent?

Beim maschinellen Lernen ist der Gradient-Descent-Algorithmus einer der am häufigsten verwendeten Algorithmen, und doch macht er die meisten Neulinge fassungslos. Mathematisch gesehen ist Gradient Descent ein iterativer Optimierungsalgorithmus erster Ordnung, der verwendet wird, um das lokale Minimum einer differenzierbaren Funktion zu finden. Einfach ausgedrückt wird dieser Gradientenabstiegsalgorithmus verwendet, um die Werte der Parameter (oder Koeffizienten) einer Funktion zu finden, die verwendet werden, um eine Kostenfunktion so niedrig wie möglich zu minimieren. Die Kostenfunktion wird verwendet, um den Fehler zwischen den vorhergesagten Werten und den tatsächlichen Werten eines erstellten Modells für maschinelles Lernen zu quantifizieren.

Gradientenabstieg Intuition

Betrachten Sie eine große Schüssel, in der Sie normalerweise Obst aufbewahren oder Müsli essen würden. Diese Schale ist die Kostenfunktion (f).

Nun wird eine zufällige Koordinate auf irgendeinem Teil der Oberfläche der Schüssel die aktuellen Werte der Koeffizienten der Kostenfunktion sein. Der Boden der Schale ist der beste Koeffizientensatz und das Minimum der Funktion.

Hier besteht das Ziel darin, die unterschiedlichen Werte der Koeffizienten bei jeder Iteration zu berechnen, die Kosten zu bewerten und die Koeffizienten auszuwählen, die einen besseren Kostenfunktionswert (niedrigeren Wert) haben. Bei mehreren Iterationen würde sich herausstellen, dass der Boden der Schale die besten Koeffizienten zum Minimieren der Kostenfunktion aufweist.

Auf diese Weise funktioniert der Gradient-Descent-Algorithmus so, dass er zu minimalen Kosten führt.

Nehmen Sie online am Machine Learning-Kurs der weltbesten Universitäten teil – Master, Executive Post Graduate Programs und Advanced Certificate Program in ML & AI, um Ihre Karriere zu beschleunigen.

Gradientenabstiegsverfahren

Dieser Prozess des Gradientenabstiegs beginnt mit der anfänglichen Zuordnung von Werten zu den Koeffizienten der Kostenfunktion. Dies kann entweder ein Wert nahe 0 oder ein kleiner zufälliger Wert sein.

Koeffizient = 0,0

Als nächstes werden die Kosten der Koeffizienten erhalten, indem sie auf die Kostenfunktion angewendet und die Kosten berechnet werden.

Kosten = f(Koeffizient)

Dann wird die Ableitung der Kostenfunktion berechnet. Diese Ableitung der Kostenfunktion wird durch das mathematische Konzept der Differentialrechnung erhalten. Es gibt uns die Steigung der Funktion an dem gegebenen Punkt, an dem ihre Ableitung berechnet wird. Diese Steigung wird benötigt, um zu wissen, in welche Richtung der Koeffizient in der nächsten Iteration verschoben werden muss, um einen niedrigeren Kostenwert zu erhalten. Dies geschieht durch Beobachtung des Vorzeichens der berechneten Ableitung.

Delta = Derivat (Kosten)

Sobald wir von der berechneten Ableitung wissen, welche Richtung bergab ist, müssen wir die Koeffizientenwerte aktualisieren. Dafür wird ein Parameter, der als Lernparameter bekannt ist, Alpha (α) verwendet. Hiermit wird gesteuert, inwieweit sich die Koeffizienten bei jeder Aktualisierung ändern können.

Koeffizient = Koeffizient – ​​(alpha * delta)

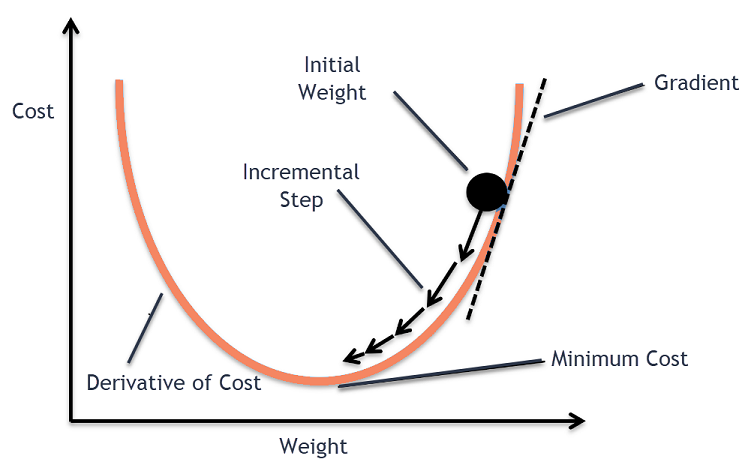
Quelle

Auf diese Weise wird dieser Vorgang wiederholt, bis die Kosten der Koeffizienten gleich 0,0 oder nahe genug bei Null sind. Dies ist das Verfahren für den Gradientenabstiegsalgorithmus.

Arten von Gradientenabstiegsalgorithmen

In der heutigen Zeit gibt es drei grundlegende Arten von Gradient Descent, die in modernen maschinellen Lern- und Deep-Learning-Algorithmen verwendet werden. Der Hauptunterschied zwischen jedem dieser 3 Typen ist der Rechenaufwand und die Effizienz. Abhängig von der verwendeten Datenmenge, Zeitkomplexität und Genauigkeit sind die folgenden drei Typen.

1. Batch-Gradientenabstieg
2. Stochastischer Gradientenabstieg
3. Mini-Batch-Gradientenabstieg

Batch-Gradientenabstieg

Dies ist die erste und grundlegende Version der Gradient Descent-Algorithmen, bei der der gesamte Datensatz auf einmal verwendet wird, um die Kostenfunktion und ihren Gradienten zu berechnen. Da für eine einzige Aktualisierung der gesamte Datensatz auf einmal verwendet wird, kann die Berechnung des Gradienten bei dieser Art sehr langsam sein und ist bei Datensätzen, die nicht über die Speicherkapazität des Geräts hinausgehen, nicht möglich.

Daher wird dieser Batch-Gradientenabstiegsalgorithmus nur für kleinere Datensätze verwendet, und wenn die Anzahl der Trainingsbeispiele groß ist, wird der Batch-Gradientenabstieg nicht bevorzugt. Stattdessen werden die Algorithmen Stochastic und Mini Batch Gradient Descent verwendet.

Stochastischer Gradientenabstieg

Dies ist eine andere Art von Gradientenabstiegsalgorithmus, bei dem nur ein Trainingsbeispiel pro Iteration verarbeitet wird. Dabei wird im ersten Schritt der gesamte Trainingsdatensatz randomisiert. Dann wird nur ein Trainingsbeispiel zum Aktualisieren der Koeffizienten verwendet. Dies steht im Gegensatz zum Batch Gradient Descent, bei dem die Parameter (Koeffizienten) nur aktualisiert werden, wenn alle Trainingsbeispiele ausgewertet sind.

Der stochastische Gradientenabstieg (SGD) hat den Vorteil, dass diese Art der häufigen Aktualisierung eine detaillierte Verbesserungsrate liefert. In bestimmten Fällen kann sich dies jedoch als rechenintensiv herausstellen, da es nur ein Beispiel pro Iteration verarbeitet, was dazu führen kann, dass die Anzahl der Iterationen sehr groß wird.

Mini-Batch-Gradientenabstieg

Dies ist ein kürzlich entwickelter Algorithmus, der schneller ist als sowohl der Batch- als auch der Stochastic Gradient Descent-Algorithmus. Es wird meistens bevorzugt, da es eine Kombination der beiden zuvor erwähnten Algorithmen ist. Dabei trennt es den Trainingssatz in mehrere Mini-Batches und führt eine Aktualisierung für jeden dieser Batches durch, nachdem der Gradient dieses Batches berechnet wurde (wie in SGD).

Üblicherweise variiert die Chargengröße zwischen 30 und 500, aber es gibt keine feste Größe, da sie für verschiedene Anwendungen unterschiedlich ist. Selbst wenn ein riesiger Trainingsdatensatz vorhanden ist, verarbeitet dieser Algorithmus ihn daher in „b“ Mini-Batches. Daher eignet es sich für große Datensätze mit einer geringeren Anzahl von Iterationen.

Wenn „m“ die Anzahl der Trainingsbeispiele ist, dann ist der Mini-Batch-Gradientenabstieg ähnlich wie der Batch-Gradientenabstieg-Algorithmus, wenn b==m ist.

Varianten des Gradientenabstiegs beim maschinellen Lernen

Auf dieser Grundlage für Gradient Descent wurden mehrere andere Algorithmen entwickelt, die daraus entwickelt wurden. Einige davon sind unten zusammengefasst.

Vanille-Gradientenabstieg

Dies ist eine der einfachsten Formen der Gradient Descent-Technik. Der Name Vanille bedeutet rein oder unverfälscht. Dabei werden kleine Schritte in Richtung der Minima gemacht, indem die Steigung der Kostenfunktion berechnet wird. Ähnlich wie beim oben genannten Algorithmus ist die Aktualisierungsregel gegeben durch:

Koeffizient = Koeffizient – ​​(alpha * delta)

Steigungsabstieg mit Schwung

In diesem Fall ist der Algorithmus so, dass wir die vorherigen Schritte kennen, bevor wir den nächsten Schritt machen. Dies geschieht durch die Einführung eines neuen Begriffs, der das Produkt der vorherigen Aktualisierung und einer Konstante ist, die als Momentum bekannt ist. Dabei ist die Gewichtsaktualisierungsregel gegeben durch

Update = Alpha * Delta

Geschwindigkeit = vorherige_aktualisierung * Impuls

Koeffizient = Koeffizient + Geschwindigkeit – aktualisieren

ADAGRAD

Der Begriff ADAGRAD steht für Adaptive Gradient Algorithm. Wie der Name schon sagt, verwendet es eine adaptive Technik, um die Gewichtungen zu aktualisieren. Dieser Algorithmus ist besser für spärliche Daten geeignet. Diese Optimierung ändert ihre Lernraten in Abhängigkeit von der Häufigkeit der Parameteraktualisierungen während des Trainings. Zum Beispiel werden die Parameter mit höheren Gradienten so eingestellt, dass sie eine langsamere Lernrate haben, damit wir am Ende nicht über den Mindestwert hinausschießen. In ähnlicher Weise haben niedrigere Gradienten eine schnellere Lernrate, um schneller trainiert zu werden.

ADAM

Noch ein weiterer adaptiver Optimierungsalgorithmus, der seine Wurzeln im Gradient Descent-Algorithmus hat, ist ADAM, was für Adaptive Moment Estimation steht. Es ist eine Kombination aus ADAGRAD und SGD mit Momentum-Algorithmen. Es basiert auf dem ADAGRAD-Algorithmus und ist weiter unten aufgebaut. Einfach ausgedrückt ist ADAM = ADAGRAD + Momentum.

Auf diese Weise wurden mehrere andere Varianten von Gradientenabstiegsalgorithmen entwickelt und werden weltweit entwickelt, wie z. B. AMSGrad, ADAMax.

Fazit

In diesem Artikel haben wir den Algorithmus hinter einem der am häufigsten verwendeten Optimierungsalgorithmen im maschinellen Lernen, den Gradientenabstiegsalgorithmen, zusammen mit seinen entwickelten Typen und Varianten gesehen.

upGrad bietet ein Executive PG-Programm in maschinellem Lernen und KI und einen Master of Science in maschinellem Lernen und KI , das Sie beim Aufbau einer Karriere unterstützen kann. In diesen Kursen werden die Notwendigkeit des maschinellen Lernens und weitere Schritte zum Sammeln von Wissen in diesem Bereich erläutert, die verschiedene Konzepte umfassen, die vom Gradientenabstieg bis zum maschinellen Lernen reichen.