Gaussian Naive Bayes: Was Sie wissen müssen?
Veröffentlicht: 2021-02-22Inhaltsverzeichnis
Gaussian Naive Bayes
Naive Bayes ist ein probabilistischer Algorithmus für maschinelles Lernen, der für viele Klassifizierungsfunktionen verwendet wird und auf dem Bayes-Theorem basiert. Gaussian Naive Bayes ist die Erweiterung von Naive Bayes. Während andere Funktionen zum Schätzen der Datenverteilung verwendet werden, ist die Gaußsche oder Normalverteilung am einfachsten zu implementieren, da Sie den Mittelwert und die Standardabweichung für die Trainingsdaten berechnen müssen.
Was ist der Naive-Bayes-Algorithmus?
Naive Bayes ist ein probabilistischer Algorithmus für maschinelles Lernen, der für verschiedene Klassifizierungsaufgaben verwendet werden kann. Typische Anwendungen von Naive Bayes sind die Klassifizierung von Dokumenten, das Filtern von Spam, Vorhersagen und so weiter. Dieser Algorithmus basiert auf den Entdeckungen von Thomas Bayes und daher auch sein Name.
Der Name „naiv“ wird verwendet, weil der Algorithmus Merkmale in sein Modell einbaut, die voneinander unabhängig sind. Änderungen des Werts eines Merkmals wirken sich nicht direkt auf den Wert eines anderen Merkmals des Algorithmus aus. Der Hauptvorteil des Naive-Bayes-Algorithmus besteht darin, dass es sich um einen einfachen, aber leistungsstarken Algorithmus handelt.
Es basiert auf dem Wahrscheinlichkeitsmodell, bei dem der Algorithmus einfach codiert werden kann und Vorhersagen schnell in Echtzeit erfolgen. Daher ist dieser Algorithmus die typische Wahl, um reale Probleme zu lösen, da er so eingestellt werden kann, dass er sofort auf Benutzeranfragen reagiert. Aber bevor wir tief in Naive Bayes und Gaußian Naive Bayes eintauchen, müssen wir wissen, was mit bedingter Wahrscheinlichkeit gemeint ist.
Bedingte Wahrscheinlichkeit erklärt
Anhand eines Beispiels können wir die bedingte Wahrscheinlichkeit besser verstehen. Wenn Sie eine Münze werfen, beträgt die Wahrscheinlichkeit, dass Sie weiterkommen oder Zahl haben, 50 %. Ebenso beträgt die Wahrscheinlichkeit, beim Würfeln mit Gesichtern eine 4 zu erhalten, 1/6 oder 0,16.
Wenn wir ein Kartenspiel nehmen, wie hoch ist die Wahrscheinlichkeit, dass wir eine Dame bekommen, vorausgesetzt, es ist ein Pik? Da die Bedingung bereits festgelegt ist, dass es ein Pik sein muss, wird der Nenner oder der Auswahlsatz 13. Es gibt nur eine Pik-Dame, daher wird die Wahrscheinlichkeit, eine Pik-Dame zu ziehen, 1/13 = 0,07.

Die bedingte Wahrscheinlichkeit des Ereignisses A bei Ereignis B bedeutet die Wahrscheinlichkeit des Eintretens von Ereignis A unter der Voraussetzung, dass Ereignis B bereits eingetreten ist. Mathematisch kann die bedingte Wahrscheinlichkeit von A gegeben B als P[A|B] = P[A AND B] / P[B] bezeichnet werden.
Betrachten wir ein wenig komplexes Beispiel. Nehmen Sie eine Schule mit insgesamt 100 Schülern. Diese Bevölkerungsgruppe kann in 4 Kategorien unterteilt werden: Schüler, Lehrer, Männer und Frauen. Betrachten Sie die folgende Tabelle:
| Weiblich | Männlich | Gesamt | |
| Lehrer | 8 | 12 | 20 |
| Student | 32 | 48 | 80 |
| Gesamt | 40 | 50 | 100 |
Wie groß ist hier die bedingte Wahrscheinlichkeit, dass ein bestimmter Bewohner der Schule ein Lehrer ist, wenn man davon ausgeht, dass er ein Mann ist?
Um dies zu berechnen, müssen Sie die Unterpopulation von 60 Männern filtern und bis zu den 12 männlichen Lehrern aufschlüsseln.
Die erwartete bedingte Wahrscheinlichkeit P[Lehrer | Männlich] = 12/60 = 0,2
P (Lehrer | Männlich) = P (Lehrer ∩ Männlich) / P(Männlich) = 12/60 = 0,2
Dies kann als Lehrer(A) und Mann(B) geteilt durch Mann(B) dargestellt werden. In ähnlicher Weise kann auch die bedingte Wahrscheinlichkeit von B bei A berechnet werden. Die Regel, die wir für Naive Bayes verwenden, lässt sich aus den folgenden Notationen ableiten:
P (A | B) = P (A ∩ B) / P(B)
P (B | A) = P (A ∩ B) / P(A)
Die Bayes-Regel
In der Bayes-Regel gehen wir von P (X | Y), das aus dem Trainingsdatensatz gefunden werden kann, um P (Y | X) zu finden. Um dies zu erreichen, müssen Sie in den obigen Formeln lediglich A und B durch X und Y ersetzen. Für Beobachtungen wäre X die bekannte Variable und Y die unbekannte Variable. Für jede Zeile des Datensatzes müssen Sie die Wahrscheinlichkeit von Y berechnen, vorausgesetzt, dass X bereits aufgetreten ist.
Aber was passiert, wenn es mehr als 2 Kategorien in Y gibt? Wir müssen die Wahrscheinlichkeit jeder Y-Klasse berechnen, um die Gewinnerklasse herauszufinden.
Durch die Bayes-Regel gehen wir von P (X | Y) zu P (Y | X)
Aus Trainingsdaten bekannt: P (X | Y) = P (X ∩ Y) / P(Y)
P (Evidenz | Ergebnis)
Unbekannt – für Testdaten vorherzusagen: P (Y | X) = P (X ∩ Y) / P(X)
P (Ergebnis | Nachweis)

Bayes-Regel = P (Y | X) = P (X | Y) * P (Y) / P (X)
Die naiven Bayes
Die Bayes-Regel liefert die Formel für die Wahrscheinlichkeit von Y bei gegebener Bedingung X. Aber in der realen Welt kann es mehrere X-Variablen geben. Wenn Sie unabhängige Merkmale haben, kann die Bayes-Regel auf die Naive-Bayes-Regel erweitert werden. Die X sind unabhängig voneinander. Die Naive-Bayes-Formel ist stärker als die Bayes-Formel
Gaussian Naive Bayes
Bisher haben wir gesehen, dass die X in Kategorien sind, aber wie berechnet man Wahrscheinlichkeiten, wenn X eine kontinuierliche Variable ist? Wenn wir davon ausgehen, dass X einer bestimmten Verteilung folgt, können Sie die Wahrscheinlichkeitsdichtefunktion dieser Verteilung verwenden, um die Wahrscheinlichkeit von Likelihoods zu berechnen.
Wenn wir davon ausgehen, dass X einer Gaußschen oder Normalverteilung folgen, müssen wir die Wahrscheinlichkeitsdichte der Normalverteilung ersetzen und sie Gaussian Naive Bayes nennen. Um diese Formel zu berechnen, benötigen Sie den Mittelwert und die Varianz von X.
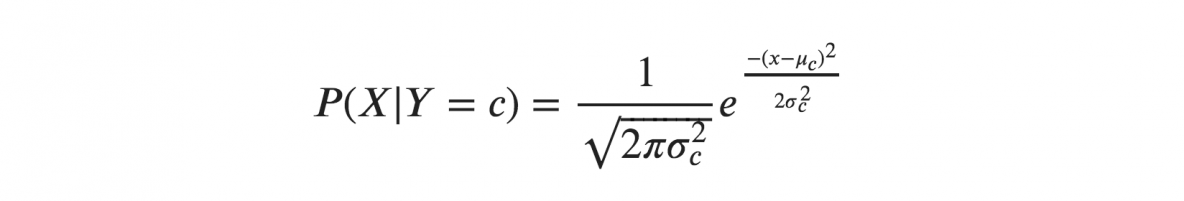
In den obigen Formeln sind Sigma und Mu die Varianz und der Mittelwert der kontinuierlichen Variablen X, berechnet für eine gegebene Klasse c von Y.
Darstellung für Gaussian Naive Bayes
Die obige Formel berechnete die Wahrscheinlichkeiten für Eingabewerte für jede Klasse durch eine Häufigkeit. Wir können den Mittelwert und die Standardabweichung von x für jede Klasse für die gesamte Verteilung berechnen.
Das bedeutet, dass wir neben den Wahrscheinlichkeiten für jede Klasse auch den Mittelwert und die Standardabweichung für jede Eingangsvariable der Klasse speichern müssen.
Mittelwert(x) = 1/n * Summe(x)
wobei n die Anzahl der Instanzen darstellt und x der Wert der Eingabevariablen in den Daten ist.
Standardabweichung(x) = sqrt(1/n * sum(xi-mean(x)^2 ))
Hier wird die Quadratwurzel des Durchschnitts der Differenzen jedes x und der Mittelwert von x berechnet, wobei n die Anzahl der Instanzen, sum() die Summenfunktion, sqrt() die Quadratwurzelfunktion und xi ein bestimmter x-Wert ist .

Vorhersagen mit dem Gaussian Naive Bayes Model
Die Gaußsche Wahrscheinlichkeitsdichtefunktion kann verwendet werden, um Vorhersagen zu treffen, indem die Parameter durch den neuen Eingabewert der Variablen ersetzt werden, und als Ergebnis liefert die Gaußsche Funktion eine Schätzung für die Wahrscheinlichkeit des neuen Eingabewerts.
Naive Bayes-Klassifikator
Der Naive-Bayes-Klassifikator geht davon aus, dass der Wert eines Merkmals unabhängig vom Wert eines anderen Merkmals ist. Naive-Bayes-Klassifikatoren benötigen Trainingsdaten, um die für die Klassifizierung erforderlichen Parameter zu schätzen. Aufgrund des einfachen Designs und der einfachen Anwendung können Naive-Bayes-Klassifikatoren in vielen realen Szenarien geeignet sein.
Fazit
Der Gaussian Naive Bayes-Klassifikator ist eine schnelle und einfache Klassifikatortechnik, die ohne allzu großen Aufwand und mit einem guten Maß an Genauigkeit sehr gut funktioniert.
Wenn Sie mehr über KI und maschinelles Lernen erfahren möchten, schauen Sie sich das PG-Diplom in maschinellem Lernen und KI von IIIT-B & upGrad an, das für Berufstätige konzipiert ist und mehr als 450 Stunden strenge Schulungen, mehr als 30 Fallstudien und Aufgaben bietet. IIIT-B Alumni-Status, mehr als 5 praktische Schlusssteinprojekte und Arbeitsunterstützung bei Top-Unternehmen.
Lernen Sie ML-Kurse von den besten Universitäten der Welt. Erwerben Sie Master-, Executive PGP- oder Advanced Certificate-Programme, um Ihre Karriere zu beschleunigen.
Was ist ein Naive-Bayes-Algorithmus?
Naive Bayes ist ein klassischer Algorithmus für maschinelles Lernen. Naive Bayes hat seinen Ursprung in der Statistik und ist ein einfacher und leistungsfähiger Algorithmus. Naive Bayes ist eine Familie von Klassifikatoren, die auf der Anwendung einer bedingten Wahrscheinlichkeitsanalyse basieren. Bei dieser Analyse wird die bedingte Wahrscheinlichkeit eines Ereignisses unter Verwendung der Wahrscheinlichkeit jedes einzelnen Ereignisses, aus dem das Ereignis besteht, berechnet. Naive-Bayes-Klassifikatoren erweisen sich in der Praxis oft als äußerst effektiv, insbesondere wenn die Anzahl der Dimensionen des Merkmalssatzes groß ist.
Was sind die Anwendungen des Naive-Bayes-Algorithmus?
Naive Bayes wird zur Textklassifizierung, Dokumentenklassifizierung und zur Dokumentenindizierung verwendet. In naiven Buchten wird jedem möglichen Merkmal in der Vorverarbeitungsphase kein Gewicht zugewiesen, und die Gewichte werden später während des Trainings sowie der Erkennungsphasen zugewiesen. Die Grundannahme des Naive-Bayes-Algorithmus ist, dass Merkmale unabhängig sind.
Was ist der Gaußsche Naive-Bayes-Algorithmus?
Gaussian Naive Bayes ist ein probabilistischer Klassifizierungsalgorithmus, der auf der Anwendung des Bayes-Theorems mit starken Unabhängigkeitsannahmen basiert. Im Zusammenhang mit der Klassifizierung bezieht sich Unabhängigkeit auf die Idee, dass das Vorhandensein eines Werts eines Merkmals das Vorhandensein eines anderen nicht beeinflusst (im Gegensatz zur Unabhängigkeit in der Wahrscheinlichkeitstheorie). Naiv bezieht sich auf die Verwendung einer Annahme, dass die Merkmale eines Objekts voneinander unabhängig sind. Im Zusammenhang mit maschinellem Lernen sind naive Bayes-Klassifikatoren dafür bekannt, sehr ausdrucksstark, skalierbar und ziemlich genau zu sein, aber ihre Leistung verschlechtert sich schnell mit dem Wachstum des Trainingssatzes. Eine Reihe von Merkmalen tragen zum Erfolg von naiven Bayes-Klassifikatoren bei. Am bemerkenswertesten ist, dass sie keine Anpassung der Parameter des Klassifizierungsmodells erfordern, gut mit der Größe des Trainingsdatensatzes skalieren und kontinuierliche Merkmale problemlos verarbeiten können.
