Verschiedene Arten von Regressionsmodellen, die Sie kennen müssen

Regressionsprobleme sind beim maschinellen Lernen alltäglich, und die gebräuchlichste Technik zu ihrer Lösung ist die Regressionsanalyse. Es basiert auf Datenmodellierung und beinhaltet das Ausarbeiten der am besten geeigneten Linie, die durch alle Datenpunkte verläuft, so dass der Abstand zwischen der Linie und jedem Datenpunkt minimal ist. Während es viele verschiedene Regressionsanalysetechniken gibt, sind die lineare und die logistische Regression die bekanntesten. Die Art des Regressionsanalysemodells, das wir verwenden, hängt schließlich von der Art der betroffenen Daten ab.

Lassen Sie uns mehr über die Regressionsanalyse und die verschiedenen Arten von Regressionsanalysemodellen erfahren.

Was ist Regressionsanalyse?

Die Regressionsanalyse ist eine prädiktive Modellierungstechnik zur Bestimmung der Beziehung zwischen den abhängigen (Ziel-)Variablen und den unabhängigen Variablen in einem Datensatz. Es wird normalerweise verwendet, wenn die Zielvariable kontinuierliche Werte enthält und die abhängigen und unabhängigen Variablen eine lineare oder nichtlineare Beziehung teilen. Daher finden Techniken der Regressionsanalyse Anwendung bei der Bestimmung der kausalen Wirkungsbeziehung zwischen Variablen, Zeitreihenmodellierung und Prognose. Beispielsweise lässt sich der Zusammenhang zwischen Umsatz und Werbeausgaben eines Unternehmens am besten mit Hilfe der Regressionsanalyse untersuchen.

Arten der Regressionsanalyse

Es gibt viele verschiedene Arten von Regressionsanalysetechniken, die wir verwenden können, um Vorhersagen zu treffen. Darüber hinaus wird die Verwendung jeder Technik von Faktoren wie der Anzahl der unabhängigen Variablen, der Form der Regressionslinie und der Art der abhängigen Variablen bestimmt.

Lassen Sie uns einige der am häufigsten verwendeten Regressionsanalysemethoden verstehen:

1. Lineare Regression

Die lineare Regression ist die bekannteste Modellierungstechnik und geht von einer linearen Beziehung zwischen einer abhängigen Variablen (Y) und einer unabhängigen Variablen (X) aus. Dieser lineare Zusammenhang wird anhand einer Regressionsgerade, auch Best-Fit-Gerade genannt, hergestellt. Die lineare Beziehung wird durch die Gleichung Y = c+m*X + e dargestellt, wobei „c“ der Schnittpunkt, „m“ die Steigung der Geraden und „e“ der Fehlerterm ist.

Das lineare Regressionsmodell kann einfach (mit einer abhängigen und einer unabhängigen Variablen) oder mehrfach (mit einer abhängigen Variablen und mehr als einer unabhängigen Variablen) sein.

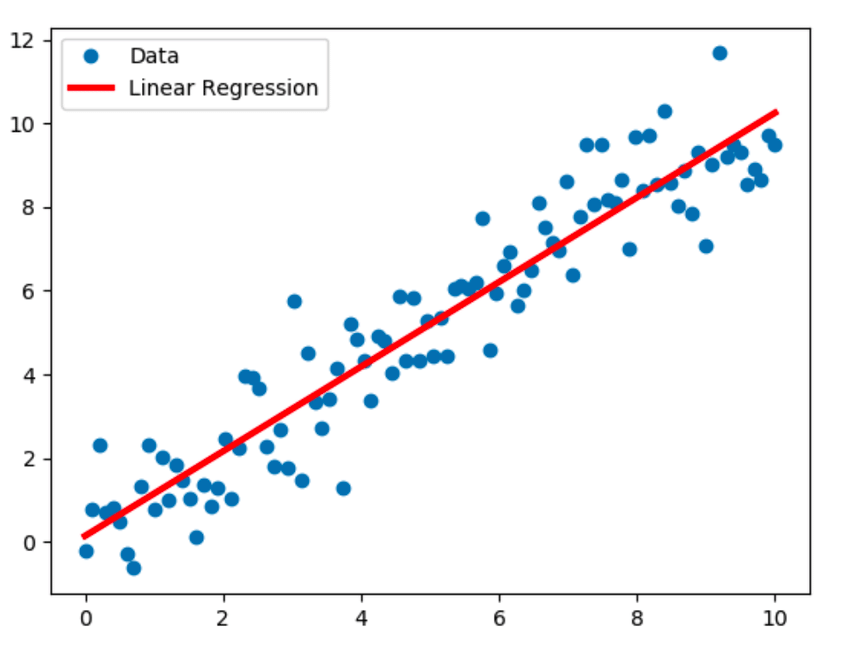
Quelle

2. Logistische Regression

Die Technik der logistischen Regressionsanalyse findet Anwendung, wenn die abhängige Variable diskret ist. Mit anderen Worten, diese Technik wird verwendet, um die Wahrscheinlichkeit von sich gegenseitig ausschließenden Ereignissen abzuschätzen, wie zum Beispiel Bestanden/Nicht bestanden, Richtig/Falsch, 0/1 usw. Daher kann die Zielvariable nur einen von zwei Werten haben und eine Sigmoidkurve darstellen seine Beziehung zur unabhängigen Variablen. Der Wert der Wahrscheinlichkeit liegt zwischen 0 und 1.

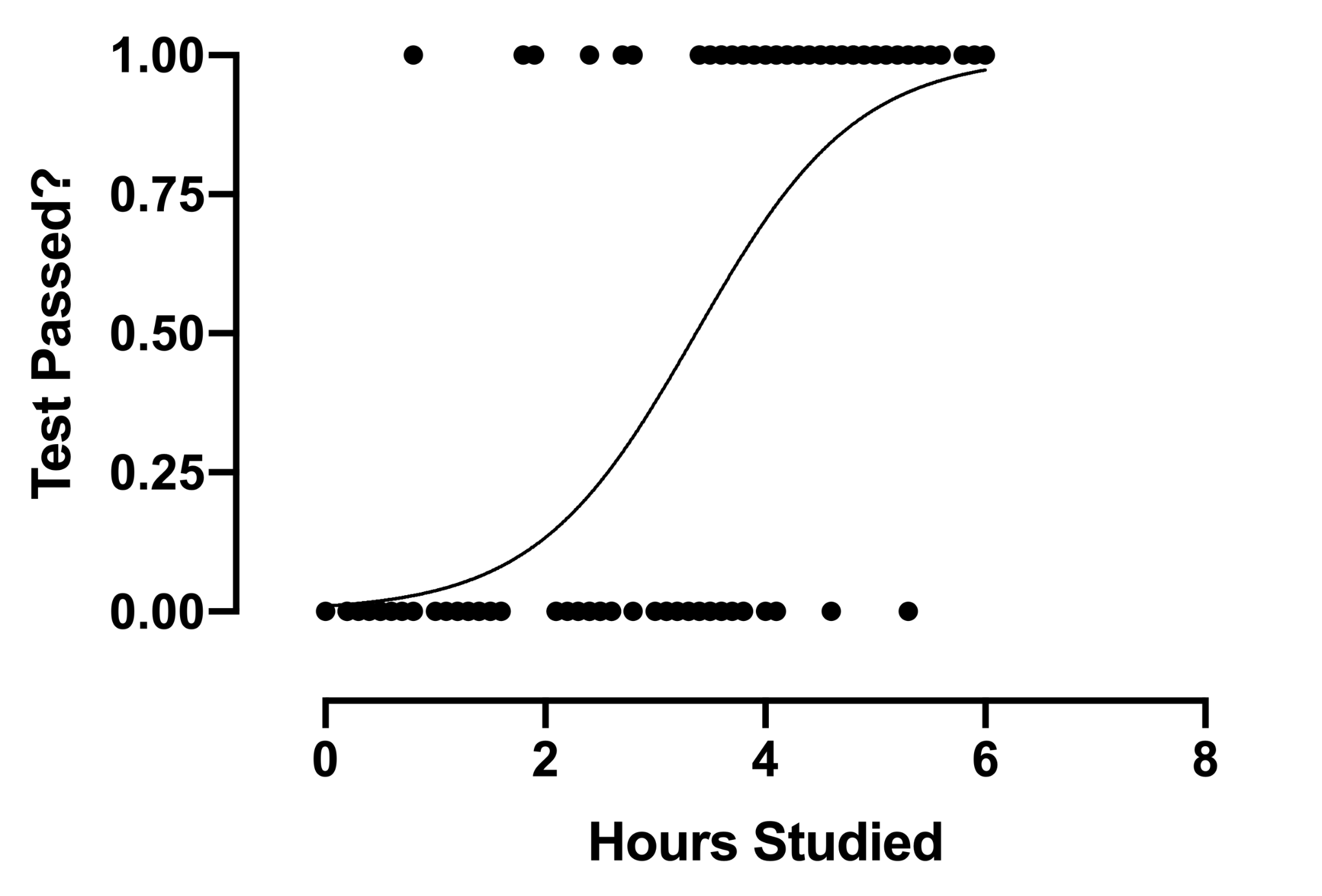
Quelle

3. Polynomische Regression

Die Technik der polynomialen Regressionsanalyse modelliert eine nichtlineare Beziehung zwischen den abhängigen und unabhängigen Variablen. Es ist eine modifizierte Form des multiplen linearen Regressionsmodells, aber die am besten passende Linie, die durch alle Datenpunkte verläuft, ist gekrümmt und nicht gerade.

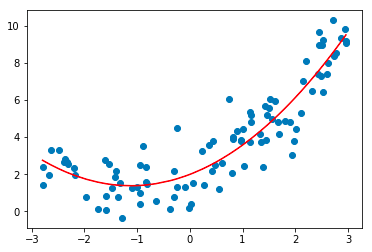
Quelle

4. Ridge-Regression

Die Technik der Ridge-Regressionsanalyse wird verwendet, wenn die Daten Multikollinearität aufweisen; das heißt, die unabhängigen Variablen sind stark korreliert. Obwohl die Schätzungen der kleinsten Quadrate bei der Multikollinearität unverzerrt sind, sind ihre Varianzen groß genug, um den beobachteten Wert vom wahren Wert abzuweichen. Die Ridge-Regression minimiert die Standardfehler, indem ein gewisses Maß an Verzerrung in die Regressionsschätzungen eingeführt wird.

Das Lambda (λ) in der Ridge-Regressionsgleichung löst das Multikollinearitätsproblem.

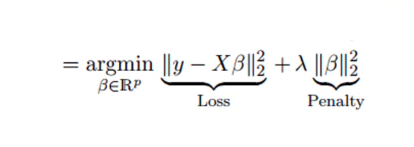
Quelle

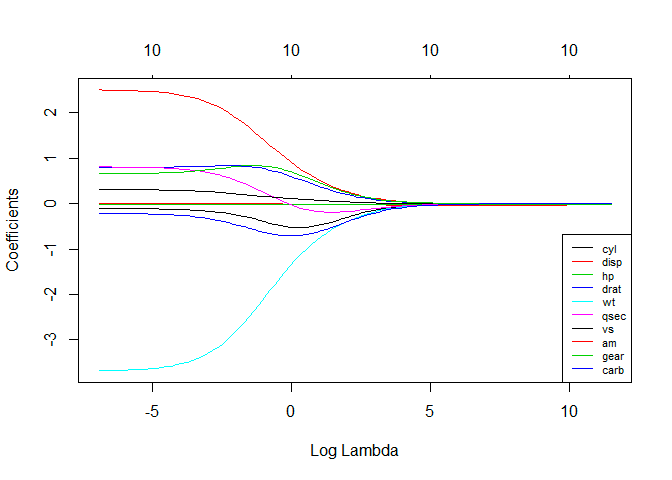
Quelle

5. Lasso-Regression

Wie bei der Ridge-Regression bestraft die Lasso-Regressionstechnik (Least Absolute Shrinkage and Selection Operator) die absolute Größe des Regressionskoeffizienten. Darüber hinaus verwendet die Lasso-Regressionstechnik eine Variablenauswahl, was dazu führt, dass die Koeffizientenwerte in Richtung des absoluten Nullpunkts schrumpfen.

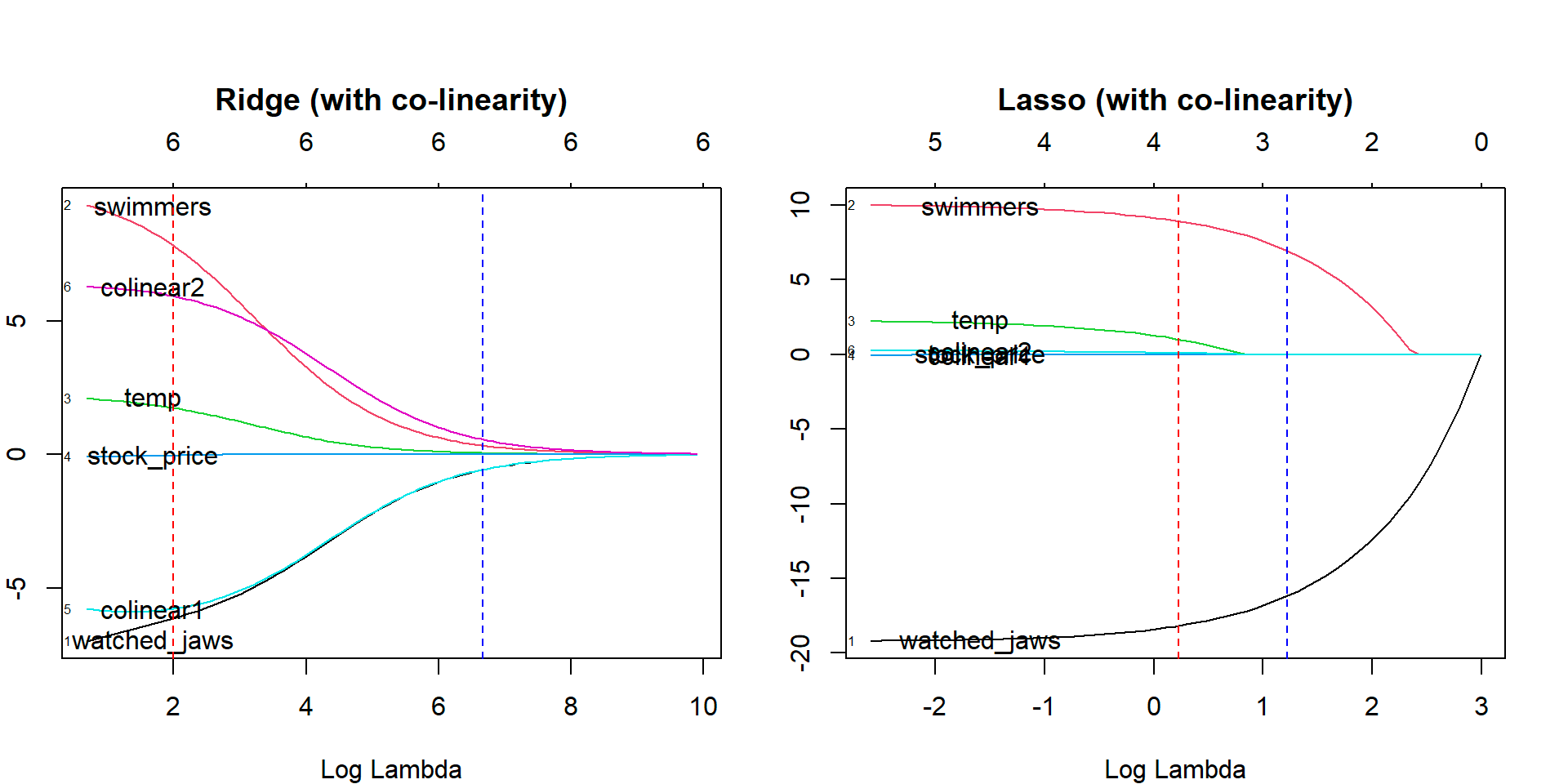
Quelle

6. Quantilregression

Die Technik der Quantilregressionsanalyse ist eine Erweiterung der linearen Regressionsanalyse. Es wird verwendet, wenn die Bedingungen für die lineare Regression nicht erfüllt sind oder die Daten Ausreißer aufweisen. Die Quantilregression findet Anwendungen in der Statistik und Ökonometrie.

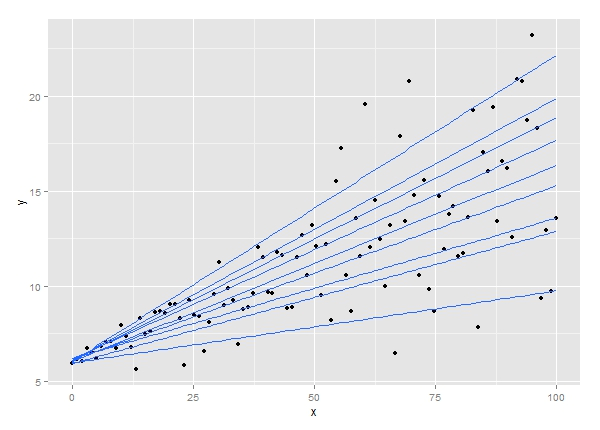
Quelle

7. Bayessche lineare Regression

Die bayessche lineare Regression ist eine der Arten von Regressionsanalysetechniken beim maschinellen Lernen, die den Satz von Bayes verwendet, um den Wert der Regressionskoeffizienten zu bestimmen. Anstatt die kleinsten Quadrate herauszufinden, bestimmt diese Technik die spätere Verteilung der Merkmale. Infolgedessen ist die Technik stabiler als die einfache lineare Regression.

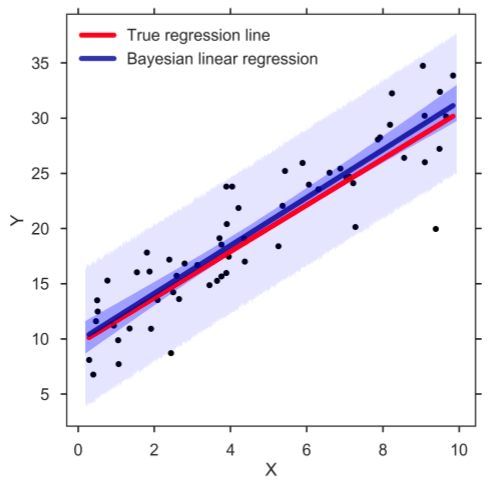
Quelle

8. Hauptkomponentenregression

Die Hauptkomponenten-Regressionstechnik wird typischerweise verwendet, um multiple Regressionsdaten mit Multikollinearität zu analysieren. Wie bei der Ridge-Regressionstechnik minimiert die Hauptkomponenten-Regressionsmethode die Standardfehler, indem sie den Regressionsschätzungen ein gewisses Maß an Verzerrung verleiht. Die Technik besteht aus zwei Schritten – zuerst wird eine Hauptkomponentenanalyse auf die Trainingsdaten angewendet, und dann werden die transformierten Stichproben verwendet, um einen Regressor zu trainieren.

9. Partielle Regression der kleinsten Quadrate

Die Regressionstechnik der partiellen Methode der kleinsten Quadrate ist eine der schnellen und effizienten Arten von Regressionsanalysetechniken, die auf Kovarianz basieren. Es ist vorteilhaft für Regressionsprobleme, bei denen die Anzahl unabhängiger Variablen hoch ist und wahrscheinlich Multikollinearität zwischen den Variablen besteht. Die Technik reduziert die Variablen auf einen kleineren Satz von Prädiktoren, die dann verwendet werden, um eine Regression durchzuführen.

10. Regression des elastischen Netzes

Die Elastic-Net-Regression-Technik ist eine Mischung aus den Ridge- und Lasso-Regressionsmodellen und ist nützlich, wenn es um stark korrelierte Variablen geht. Es verwendet die Strafen von Ridge- und Lasso-Regressionsmethoden, um die Regressionsmodelle zu regularisieren.

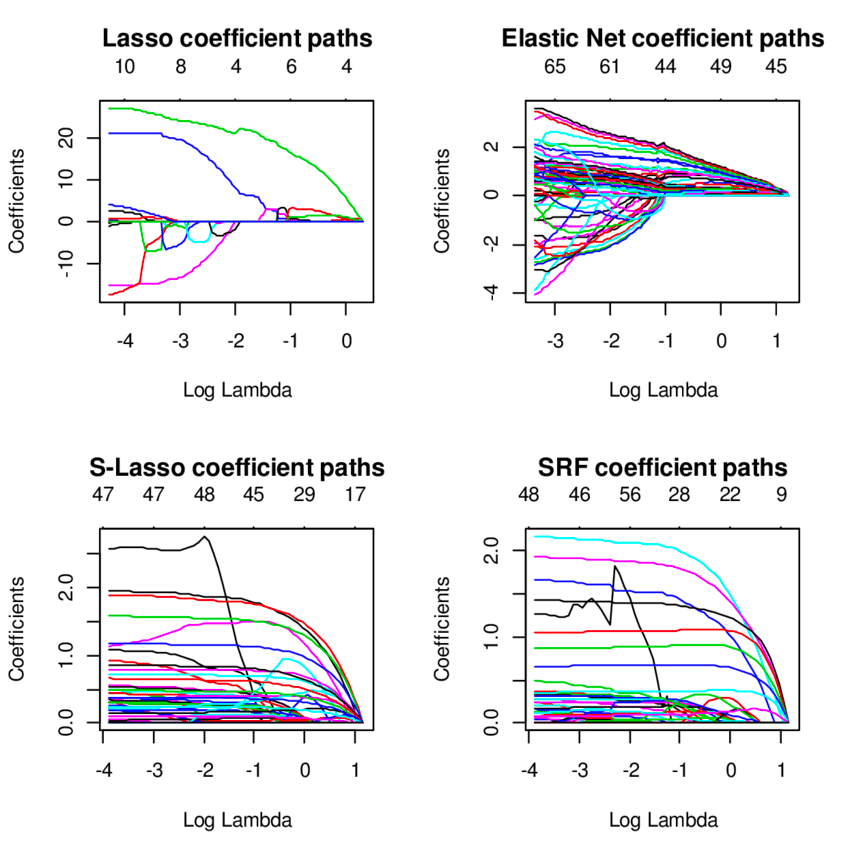
Quelle

Zusammenfassung

Abgesehen von den hier besprochenen Regressionsanalysetechniken werden beim maschinellen Lernen mehrere andere Arten von Regressionsmodellen verwendet, z. B. ökologische Regression, schrittweise Regression, Jackknife-Regression und robuste Regression. Der spezifische Anwendungsfall all dieser verschiedenen Arten von Regressionstechniken hängt von der Art der verfügbaren Daten und dem erreichbaren Genauigkeitsgrad ab. Insgesamt hat die Regressionsanalyse zwei Hauptvorteile. Diese sind wie folgt:

• Es gibt die Beziehung zwischen einer abhängigen Variablen und einer unabhängigen Variablen an.

• Es zeigt die Stärke des Einflusses unabhängiger Variablen auf eine abhängige Variable.

Weg nach vorn: Erwerben Sie einen Master of Science-Abschluss in maschinellem Lernen und KI

Suchen Sie nach einem umfassenden Online-Programm, um sich auf eine Karriere im Bereich maschinelles Lernen und künstliche Intelligenz vorzubereiten?

upGrad bietet in Zusammenarbeit mit der Liverpool John Moores University und dem IIIT Bangalore einen Master of Science-Abschluss in maschinellem Lernen und KI an, um vielseitige KI-Experten und Datenwissenschaftler hervorzubringen.

Das umfassende 20-monatige Online-Programm wurde speziell für Berufstätige entwickelt, die fortgeschrittene Konzepte und Fähigkeiten wie Deep Learning, NLP, grafische Modelle, Reinforcement Learning und dergleichen beherrschen möchten. Außerdem beabsichtigt das Programm, eine solide Grundlage in Statistik zusammen mit wichtigen Programmiersprachen und Tools wie Python, Keras, TensorFlow, Kubernetes, MySQL und mehr zu vermitteln.

Programm-Highlights:

• Master-Abschluss an der Liverpool John Moores University
• Executive PGP von IIIT Bangalore
• Über 40 Live-Sessions, über 12 Fallstudien und Projekte, 11 Programmieraufgaben, sechs Abschlussprojekte
• Über 25 Mentoring-Sitzungen mit Branchenexperten
• 360-Grad-Karrierehilfe und Lernunterstützung
• Möglichkeiten zum Peer-to-Peer-Networking

Mit einer erstklassigen Fakultät, Pädagogik, Technologie und Branchenexperten hat sich upGrad zu Südasiens größter höherer EdTech-Plattform entwickelt und mehr als 500.000 Berufstätige weltweit beeinflusst. Heute anmelden Werden Sie Teil der über 40.000 globalen Lernenden von upGrad in über 80 Ländern!