Aktualisieren von CSS-Animationen mit Bewegungskurven

Es gibt UI-Animation und dann gibt es gute UI-Animation. Gute Animation lässt Sie „Wow!“ sagen. – es ist glatt, schön und vor allem natürlich, nicht blockig, starr oder roboterhaft. Wenn Sie häufig Dribbble oder UpLabs besuchen, wissen Sie, wovon ich spreche.

Weiterführende Literatur zum Smashing:

• SVG- und CSS-Animationen mit Clip-Pfad
• Praktische Animationstechniken
• Erstellen von "handgezeichneten" Animationen mit SVG
• Die neue Webanimations-API

Bei so vielen großartigen Designern, die so schöne Animationen erstellen, würde jeder Entwickler sie natürlich in seinen eigenen Projekten nachbauen wollen. Nun, CSS bietet einige Voreinstellungen für transition-timing-function , wie beispielsweise ease-in , ease-out und ease-in-out , die ein gewisses Maß an Geschmeidigkeit und Realismus hinzufügen, aber sie sind sehr generisch, nicht wahr? Wie langweilig wäre es, wenn jede Animation im Web denselben drei Timing-Funktionen folgen würde?

Eine der Eigenschaften der transition-timing-function ist cubic-bezier(n1, n2, n3, n4) , bei der Sie vier Zahlen übergeben können, um Ihre ganz eigene Zeitfunktion zu erstellen. Gegen Ende dieses Artikels werden Sie genau wissen, was diese vier Zahlen darstellen – aber glauben Sie mir, es ist alles andere als einfach, vier Zahlen zu finden, um den Übergang zu erfassen, den Sie sich in Ihrem Kopf vorstellen. Aber dank cubic-bezier und Ceasar müssen Sie das nicht. Diese Tools bringen Bewegungskurven ins Web.

Bewegungskurven werden hauptsächlich von Animatoren (z. B. in Adobe After Effects) verwendet, um erweiterte, realistische Animationen zu erstellen. Mit cubic-bezier und Ceasar können Sie einfach die Form einer Kurve manipulieren, und diese vier Zahlen ( n1, n2, n3, n4 ) werden für Sie ausgefüllt, was absolut großartig ist! Um Bewegungskurven zu verwenden und optimal zu nutzen, müssen Sie jedoch verstehen, wie sie funktionieren, und genau das werden wir in diesem Artikel tun. Lass uns anfangen.

Bewegungskurven verstehen

Eine Bewegungskurve ist nichts anderes als ein Diagramm zwischen einer animierbaren Eigenschaft und der Zeit. Eine Bewegungskurve definiert, wie sich die Geschwindigkeit einer Animation, die unter ihrem Einfluss läuft, im Laufe der Zeit ändert.

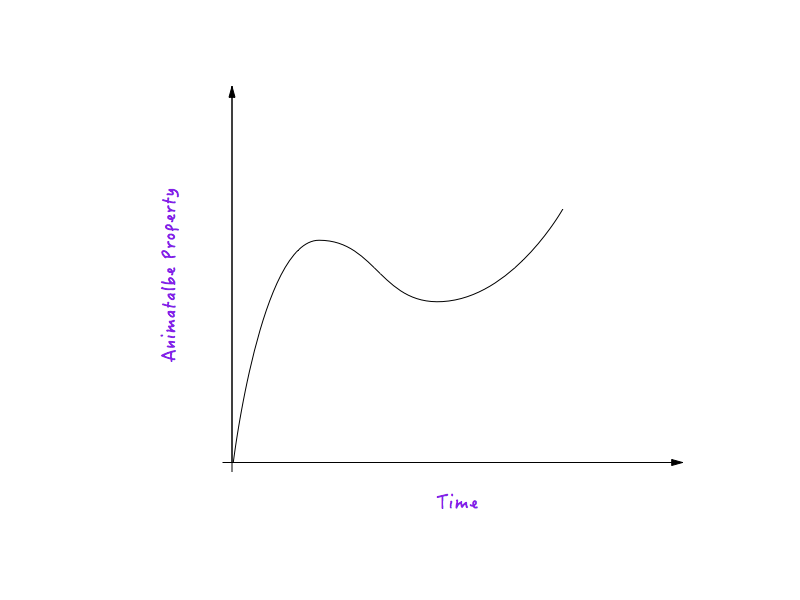
Nehmen wir distance ( translateX ) als Beispiel für eine animierbare Eigenschaft. (Die Erklärung gilt für alle anderen animierbaren Eigenschaften.)

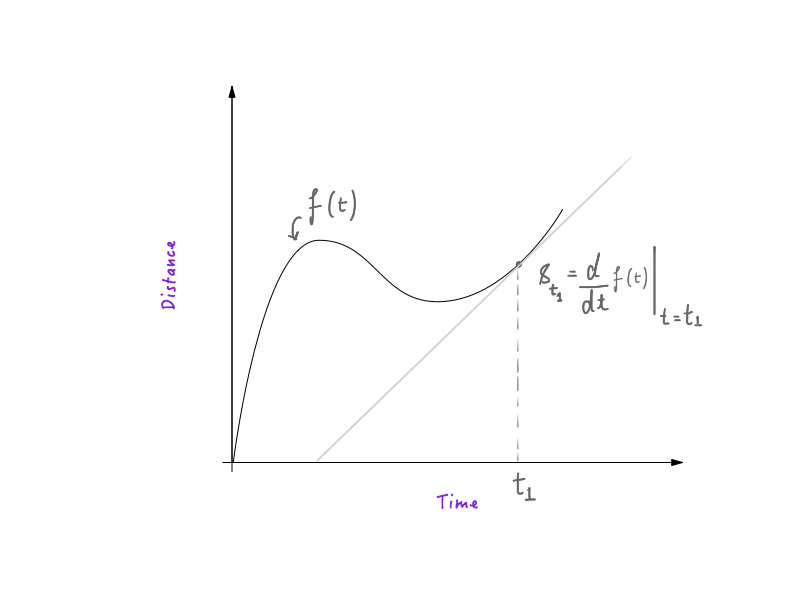
Wenn Sie Erfahrung mit Physik und grundlegenden Berechnungen haben, wissen Sie, dass es sehr einfach ist, die Geschwindigkeit aus einem Entfernungs-Zeit-Diagramm zu entschlüsseln. Die erste Ableitung der Entfernung als Funktion der Zeit in Bezug auf die Zeit ist die Geschwindigkeit, was bedeutet, dass ein Objekt, das einer Entfernungs-Zeit-Kurve folgt, an Stellen, an denen die Kurve steiler ist, eine größere Geschwindigkeit und an Stellen, an denen die Kurve flacher ist, eine geringere Geschwindigkeit hätte . Wenn Sie wissen, wie das funktioniert, großartig! Sie sind fertig und können mit dem nächsten Abschnitt fortfahren.

Nun ist mir bewusst, dass Design und Entwicklung ein vielfältiges Feld sind und nicht jeder den gleichen Hintergrund hat. Vielleicht waren die beiden obigen Absätze für Sie alles Fachjargon. Ärgern Sie sich nicht. Wir werden weitermachen und den Jargon verstehen.

Betrachten Sie das rote Kästchen unten. Lassen Sie uns hier ein wenig unbeholfen werden und das rote Kästchen „Boxy“ nennen; es wird einfacher sein, sich so darauf zu beziehen. Okay, Boxy wird sich also linear von einem Rand des Bildschirms zum anderen bewegen, und wir werden seine Bewegung analysieren.

Eine der Voreinstellungen der transition-timing-function ist linear . Um Boxy in Bewegung zu versetzen, fügen wir lediglich die folgende Klasse hinzu.

 .moveForward { transform: translateX(1000px); }

Um die Animation zu steuern, würden wir die transition für Boxy wie folgt festlegen:

 #boxy { width: 200px; height: 200px; background: red; transition-property: transform; transition-duration: 1s; transition-timing-function: linear; }

Das ist eine sehr ausführliche Methode, um transit transition . In der Realität werden Sie fast immer den transition in seiner Kurzform finden:

 #boxy { width: 200px; height: 200px; background: red; transition: transform 1s linear; }

Mal sehen, wie es geht.

Roboter, nicht wahr? Man könnte sagen, dass sich diese Bewegung roboterhaft anfühlt, weil sie linear ist, was eine absolut plausible Antwort ist. Aber könnten Sie erklären, warum? Wir können sehen, dass die linear Einstellung zu einer Roboterbewegung führt, aber was genau passiert hinter den Kulissen? Das werden wir zuerst herausfinden; Wir werden zu den Innereien gelangen und verstehen, warum sich diese Bewegung roboterhaft, blockartig und nicht natürlich anfühlt.

Beginnen wir damit, Boxys Bewegung grafisch darzustellen, um zu sehen, ob wir einen Einblick gewinnen können. Unser Diagramm hat zwei Achsen, die erste ist die Entfernung und die zweite die Zeit. Boxy legt in 1 Sekunde (Zeit) eine Gesamtdistanz von 1000 Pixeln (Distanz) zurück. Lassen Sie sich von der ganzen Mathematik unten nicht erschrecken – es ist sehr einfach.

Hier ist unser sehr einfacher Graph mit den erwähnten Achsen.

Im Moment ist es leer. Lassen Sie uns es mit einigen Daten füllen.

Zunächst einmal wissen wir, dass sich Boxy bei 0 Sekunden, wenn die Animation noch nicht begonnen hat, in seiner Ausgangsposition (0 Pixel) befindet. Und nachdem 1 Sekunde vergangen ist, hat Boxy insgesamt 1000 Pixel zurückgelegt und landet am gegenüberliegenden Rand des Displays.

Lassen Sie uns diese Daten in das Diagramm eintragen.

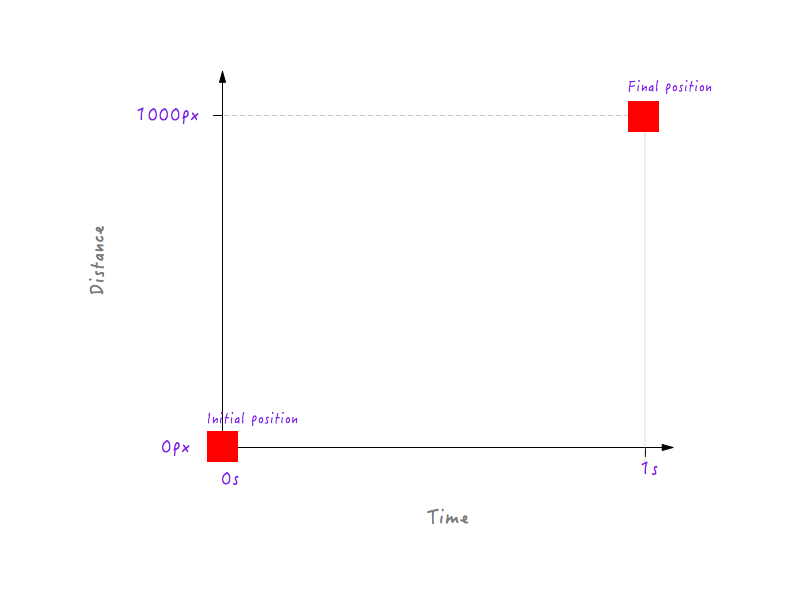
So weit, ist es gut. Aber zwei Datenpunkte reichen nicht aus – wir brauchen mehr. Die folgende Abbildung zeigt die Positionen von Boxy zu verschiedenen Zeitpunkten (alles dank meiner Hochgeschwindigkeitskamera).

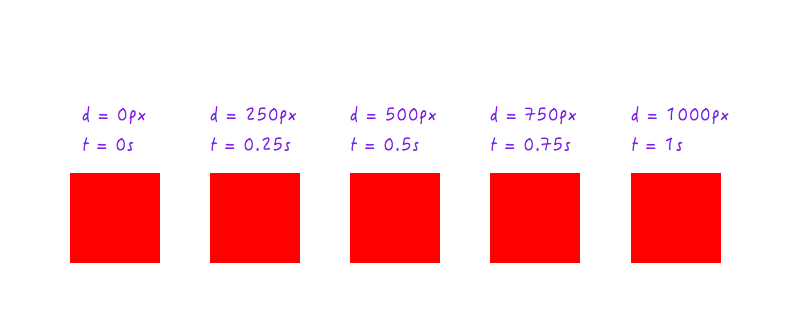
Fügen wir diese Daten unserem Diagramm hinzu.

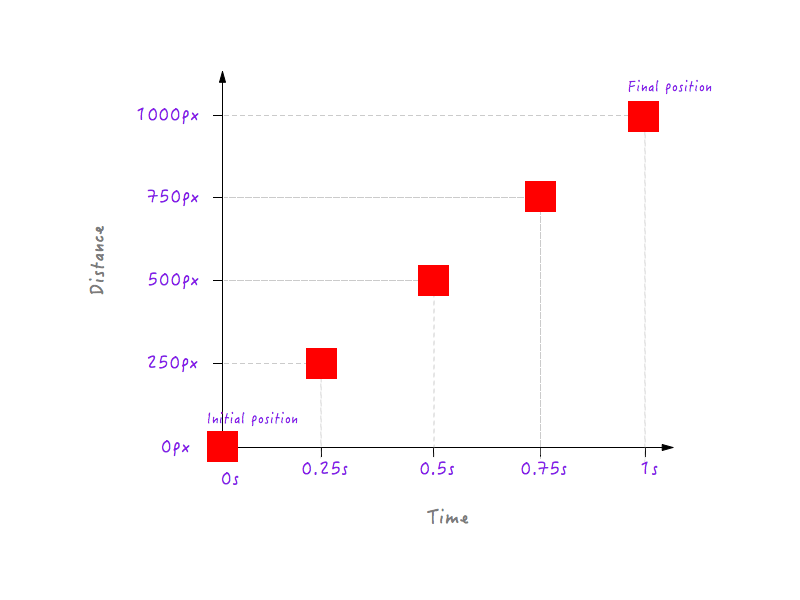
Sie könnten natürlich viel mehr Datenpunkte für verschiedene Zeiten haben (z. B. 0,375 Sekunden, 0,6 Sekunden usw.), aber was wir haben, reicht aus, um unser Diagramm zu vervollständigen. Indem wir alle Punkte zusammengefügt haben, haben wir das Diagramm vervollständigt. Gib mir fünf!

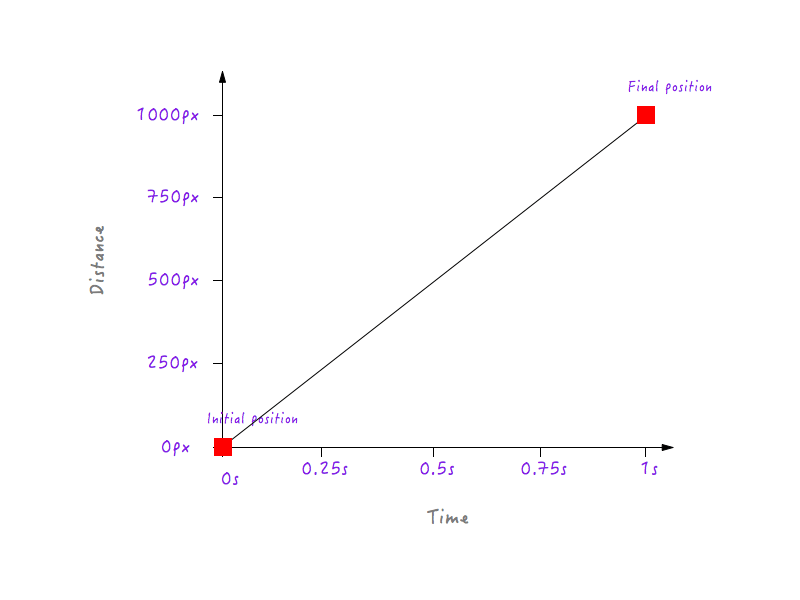
Cool, aber was sagt uns das? Denken Sie daran, dass wir unsere Untersuchung mit dem Ziel begonnen haben, zu verstehen, warum sich Boxys lineare Bewegung unnatürlich und roboterhaft anfühlt? Auf den ersten Blick sagt uns diese Grafik, die wir gerade konstruiert haben, nichts darüber. Wir müssen tiefer gehen.

Denken Sie an die Grafik und lassen Sie uns eine Minute über Geschwindigkeit sprechen. Ich weiß, dass Sie wissen, was Geschwindigkeit ist – ich möchte es nur mathematisch ausdrücken. Die Formel für die Geschwindigkeit lautet wie folgt:

Wenn also ein Auto eine Strecke von 100 Kilometern in 1 Stunde zurücklegt, sagen wir, dass seine Geschwindigkeit 100 Kilometer pro Stunde beträgt.

Wenn das Auto seine Geschwindigkeit verdoppelt, legt es die doppelte Strecke (200 Kilometer) im gleichen Intervall (1 Stunde) zurück, oder anders ausgedrückt, es legt die ursprüngliche Strecke von 100 Kilometern in der Hälfte der Zeit (0,5 Stunden) zurück. . Sinn ergeben?

Wenn das Auto seine Geschwindigkeit halbiert (d. h. um die Hälfte verlangsamt), würde es im gleichen Intervall (1 Stunde) eine Strecke von 50 Kilometern zurücklegen, oder mit anderen Worten, es würde die ursprüngliche Strecke von 100 zurücklegen Kilometer in doppelter Zeit (2 Stunden).

Toll! Lassen Sie uns damit weitermachen, wo wir aufgehört haben. Wir haben versucht herauszufinden, wie der Graph zwischen Entfernung und Zeit uns helfen kann zu verstehen, warum sich Boxys lineare Bewegung roboterhaft anfühlt.

He, warte eine Sekunde! Wir haben einen Graphen zwischen Entfernung und Zeit, und die Geschwindigkeit kann aus Entfernung und Zeit berechnet werden, nicht wahr? Versuchen wir, Boxys Geschwindigkeit in verschiedenen Zeitintervallen zu berechnen.

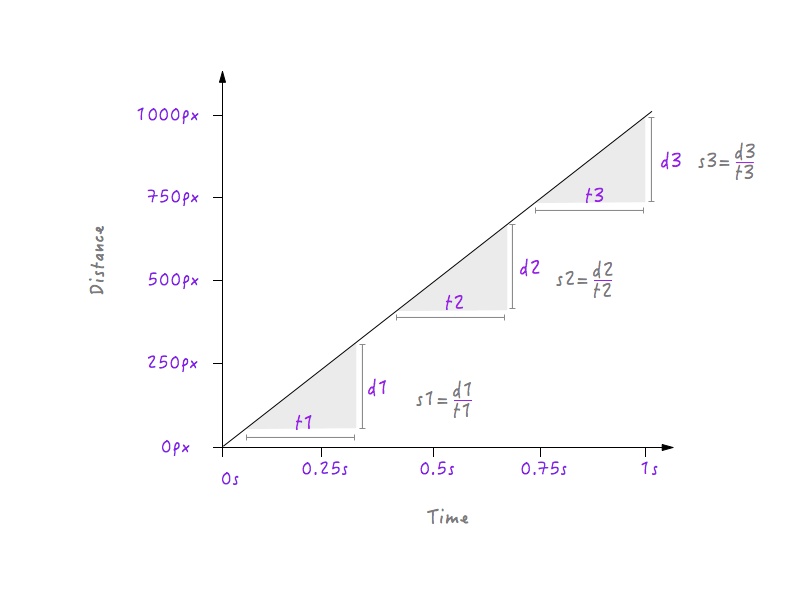
Hier habe ich drei verschiedene Zeitintervalle gewählt: eines in der Nähe des Starts, eines in der Mitte und eines am Ende in der Nähe der Endposition. Wie ersichtlich ist, hat Boxy bei allen drei Intervallen genau die gleiche Geschwindigkeit (s1 = s2 = s3) von 1000 Pixeln pro Sekunde; Das heißt, egal welches Intervall Sie in der obigen Grafik wählen, Sie werden feststellen, dass sich Boxy mit 1000 Pixeln pro Sekunde bewegt. Ist das nicht seltsam? Die Dinge im wirklichen Leben bewegen sich nicht mit konstanter Geschwindigkeit; Sie beginnen langsam, erhöhen allmählich ihre Geschwindigkeit, bewegen sich eine Weile und werden dann wieder langsamer, bevor sie anhalten, aber Boxy beginnt abrupt mit einer Geschwindigkeit von 1000 Pixeln pro Sekunde, bewegt sich mit derselben Geschwindigkeit und stoppt abrupt mit genau derselben Geschwindigkeit. Deshalb fühlt sich Boxys Bewegung roboterhaft und unnatürlich an. Wir müssen unser Diagramm ändern, um dies zu beheben. Aber bevor wir eintauchen, müssen wir wissen, wie sich Änderungen der Geschwindigkeit auf den zwischen Entfernung und Zeit gezeichneten Graphen auswirken. Bereit? Das wird spaßig.

Lassen Sie uns die Geschwindigkeit von Boxy verdoppeln und sehen, wie sich das Aussehen des Diagramms als Reaktion darauf ändert. Die ursprüngliche Geschwindigkeit von Boxy beträgt, wie wir oben berechnet haben, 1000 Pixel pro Sekunde. Da wir die Geschwindigkeit verdoppelt haben, wird Boxy nun in der Lage sein, die Distanz von 1000 Pixeln in der Hälfte der Zeit zurückzulegen – also in 0,5 Sekunden. Lassen Sie uns das in einem Diagramm darstellen.

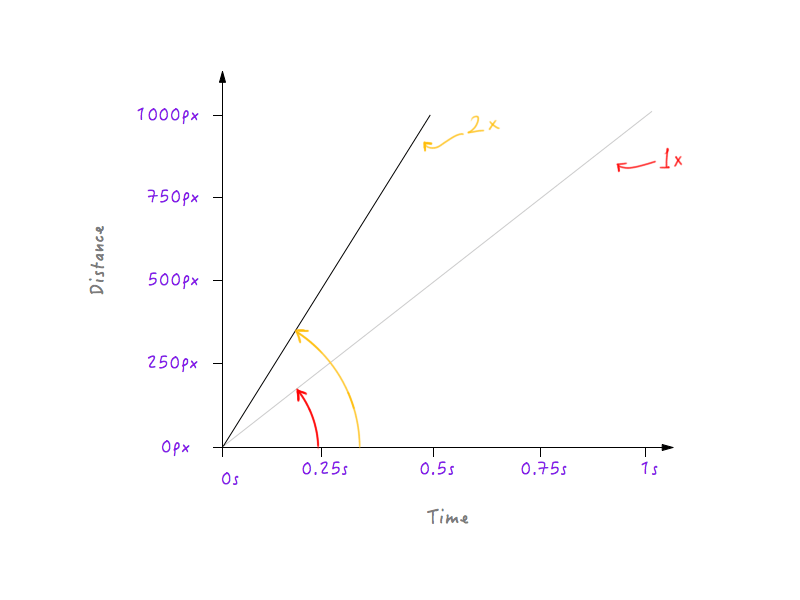
Was wäre, wenn wir die Geschwindigkeit verdreifachen würden? Boxy deckt jetzt 1000 Pixel in einem Drittel der Zeit (einer Drittelsekunde) ab.

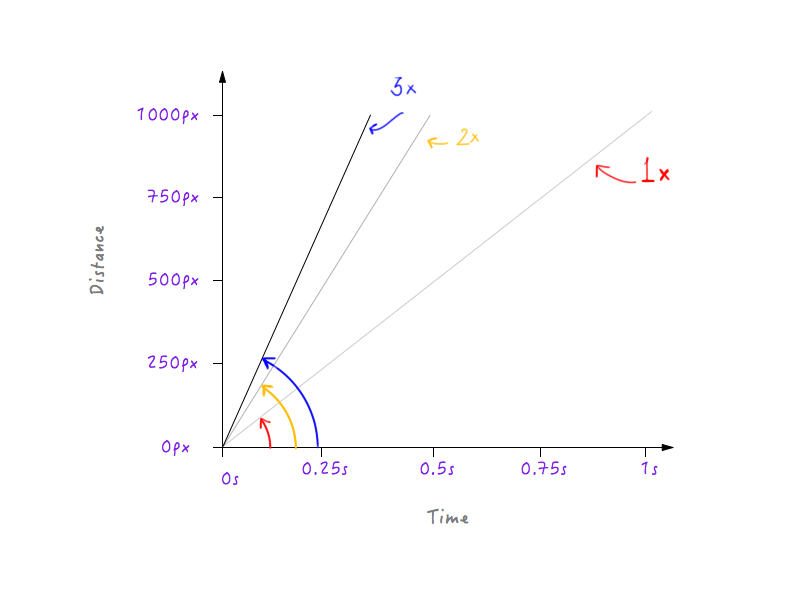
Hm, fällt dir was auf? Beachten Sie, wie bei einer Änderung des Diagramms der Winkel, den die Linie mit der Zeitachse bildet, mit zunehmender Geschwindigkeit zunimmt.

Okay, machen wir weiter und halbieren Boxys Geschwindigkeit. Die Halbierung seiner Geschwindigkeit bedeutet, dass Boxy nur 500 Pixel (die Hälfte der ursprünglichen Entfernung) in 1 Sekunde zurücklegen kann. Lassen Sie uns dies in einem Diagramm darstellen.

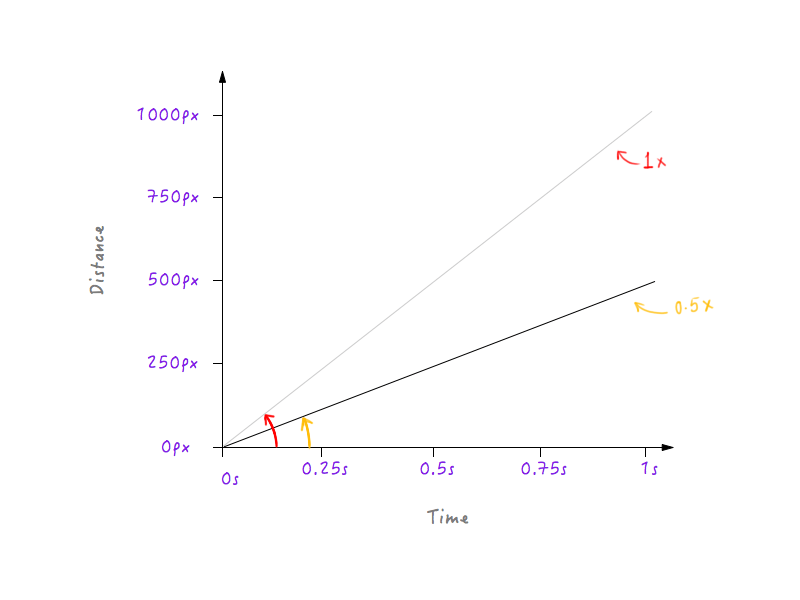
Lassen Sie uns Boxy etwas mehr verlangsamen und die Geschwindigkeit auf ein Drittel des Originals erhöhen. Boxy wird in der Lage sein, ein Drittel der ursprünglichen Distanz in 1 Sekunde zurückzulegen.

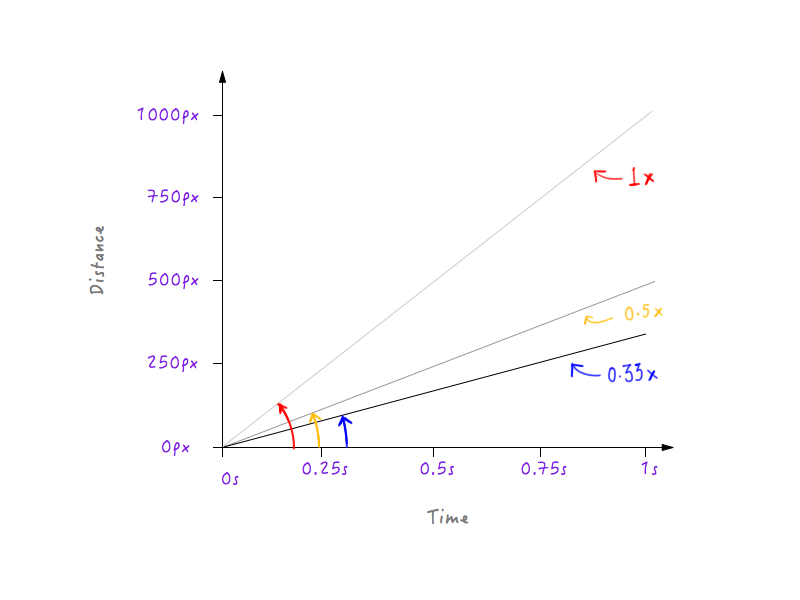
Sehen Sie ein Muster? Die Linie wird steiler und steiler, wenn wir Boxys Geschwindigkeit erhöhen, und beginnt flacher zu werden, wenn wir Boxy verlangsamen.

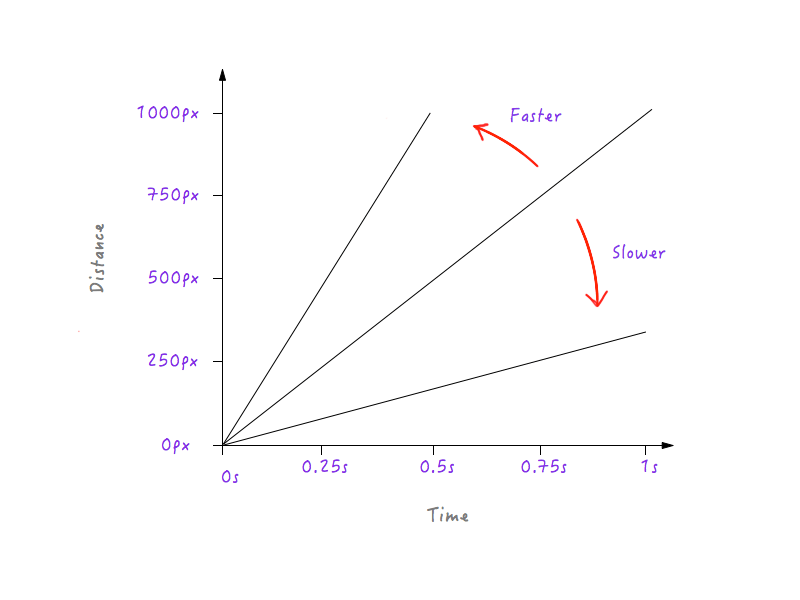
Dies ist sinnvoll, da bei einer steileren Linie ein kleiner Zeitfortschritt eine viel größere Abstandsänderung erzeugt, was eine höhere Geschwindigkeit impliziert.

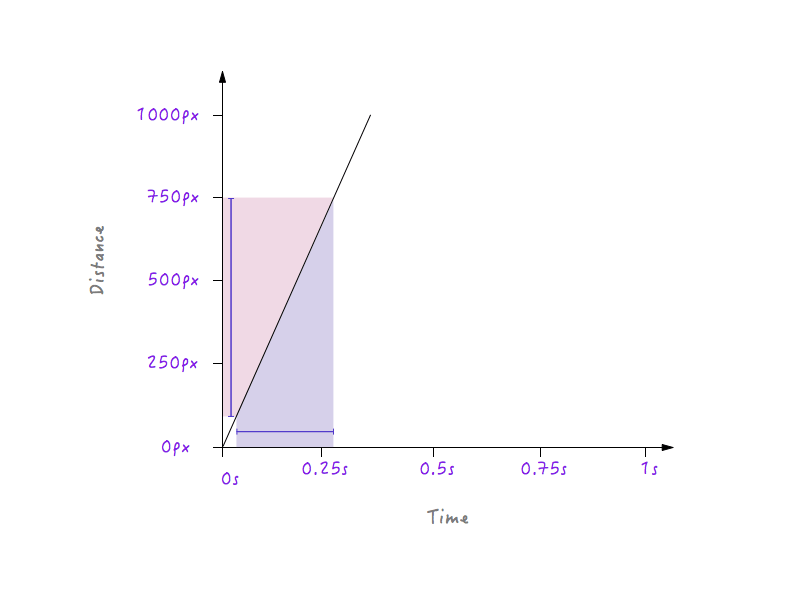
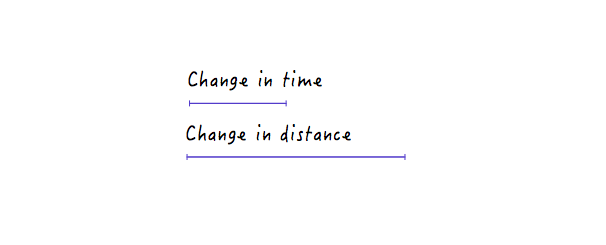
Andererseits bewirkt eine große Zeitänderung bei einer weniger steilen Linie nur eine geringe Abstandsänderung, was eine geringere Geschwindigkeit bedeutet.

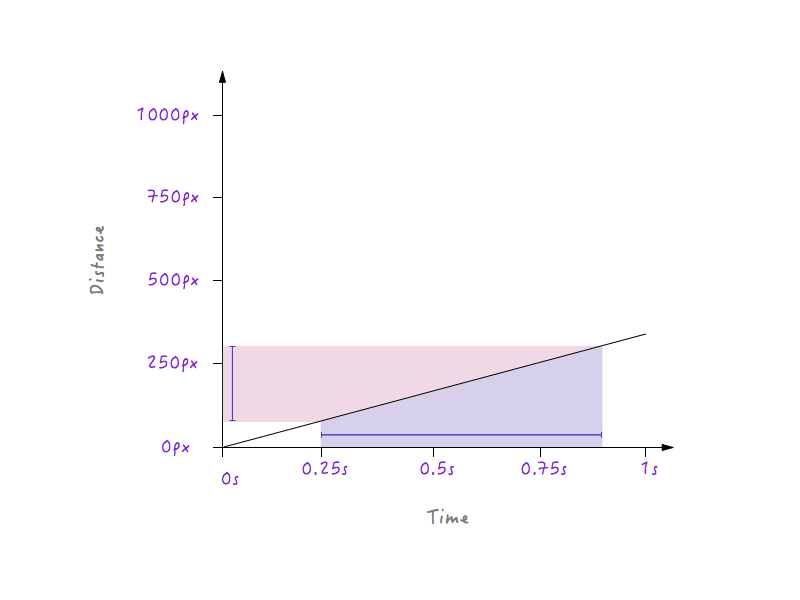
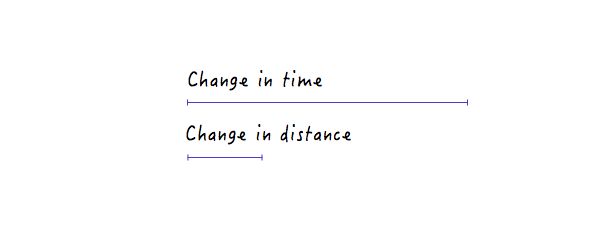
Trotz all der Änderungen, die wir vorgenommen haben, bewegt sich Boxy immer noch linear, nur mit unterschiedlichen Geschwindigkeiten. Mit unserem neu gewonnenen Wissen darüber, wie sich Änderungen der Entfernung im Verhältnis zur Zeit auf die Geschwindigkeit auswirken können, können wir jedoch experimentieren und eine Grafik zeichnen, die Boxy auf eine Weise bewegt, die natürlich und realistisch aussieht.

Gehen wir es Schritt für Schritt an. Erstens fangen die Dinge im wirklichen Leben langsam an und nehmen langsam an Geschwindigkeit zu. Also, lass uns das tun.

In allen Iterationen des unten gezeigten Diagramms werden Sie feststellen, dass die Punkte an gegenüberliegenden Ecken fest bleiben. Dies liegt daran, dass wir weder die Dauer ändern, für die die Animation ausgeführt wird, noch die Entfernung, die Boxy zurücklegt.

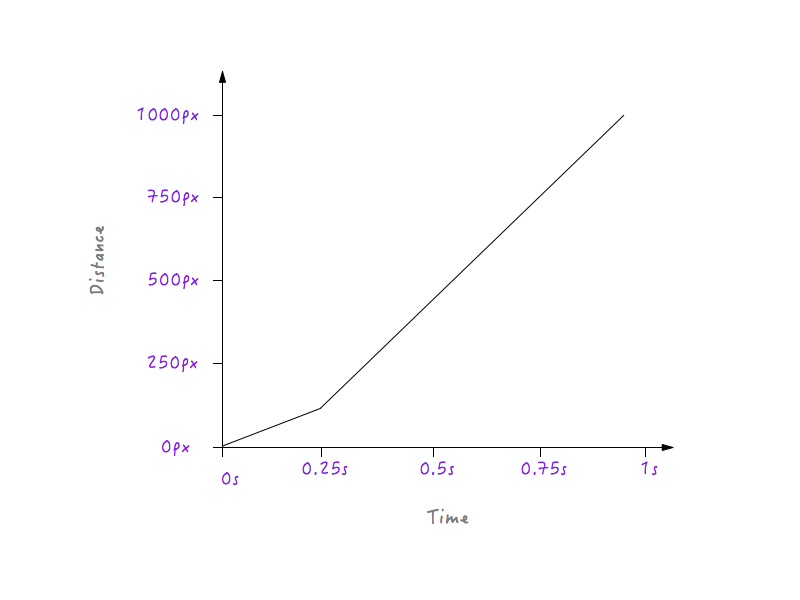
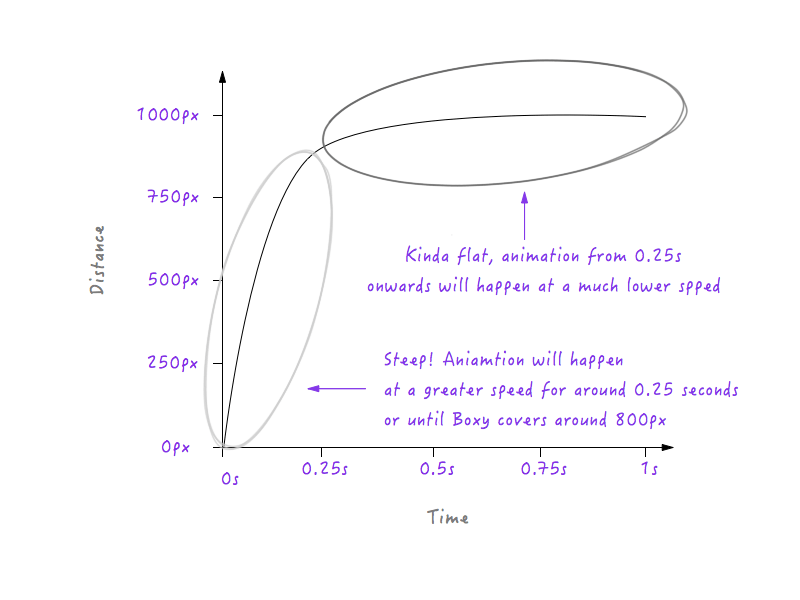
Wenn Boxy dem obigen Diagramm folgen soll, bewegt es sich 0,25 Sekunden lang mit einer langsameren Geschwindigkeit, da die Linie von 0 bis 0,25 Sekunden weniger steil ist, und schaltet dann nach 0,25 Sekunden abrupt auf eine höhere Geschwindigkeit um (der Grund dafür ist dass die Linie im Diagramm nach 0,25 Sekunden steiler wird). Wir müssen diesen Übergang jedoch glätten; Wir wollen keine Ecken – es heißt schließlich Bewegungskurve. Lassen Sie uns diese Ecke in eine Kurve umwandeln.

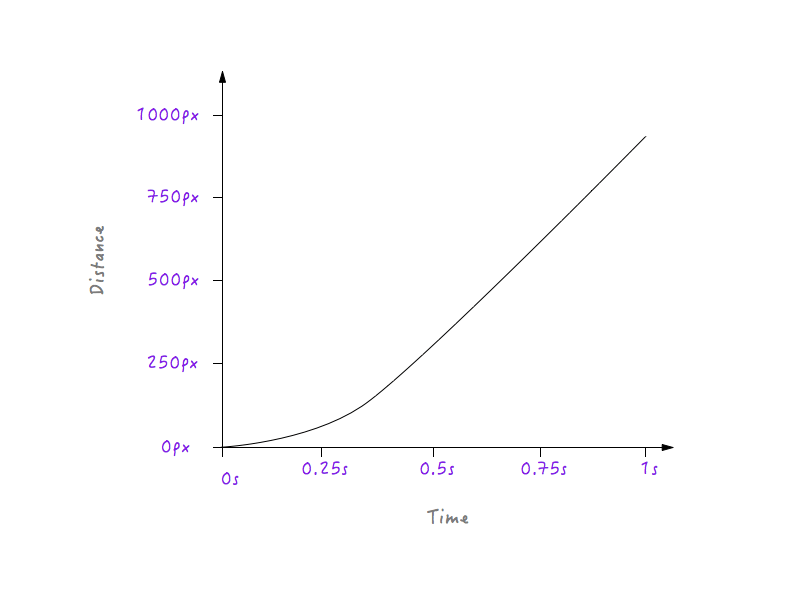
Beachten Sie den fließenden Übergang, den Boxy von der Ruhephase zu einer allmählich zunehmenden Geschwindigkeit durchläuft.

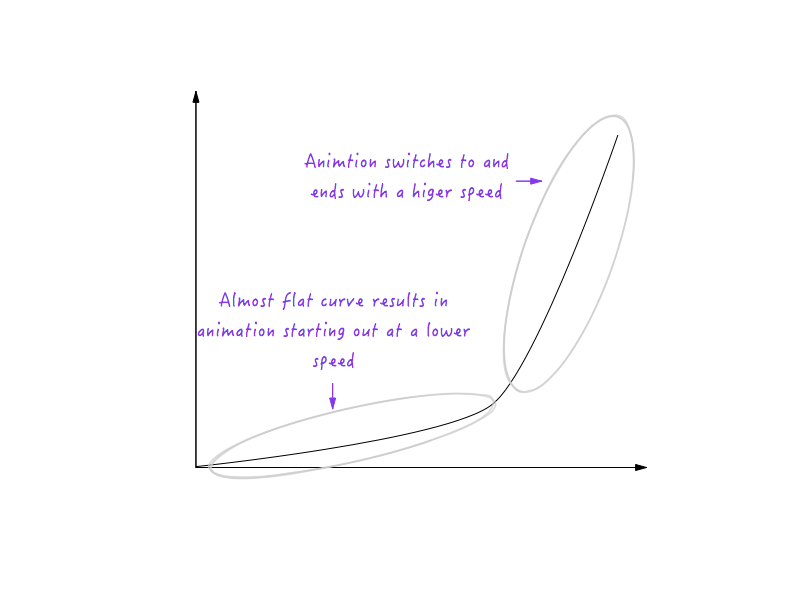
Gut! Als nächstes verlangsamen sich Objekte im wirklichen Leben zunehmend, bevor sie anhalten. Lassen Sie uns das Diagramm ändern, um dies zu erreichen. Auch hier greifen wir einen Zeitpunkt auf, nach dem wir möchten, dass Boxy langsamer wird. Wie wäre es mit etwa 0,6 Sekunden? Ich habe hier bereits die Ecke des Übergangs zu einer Kurve geglättet.

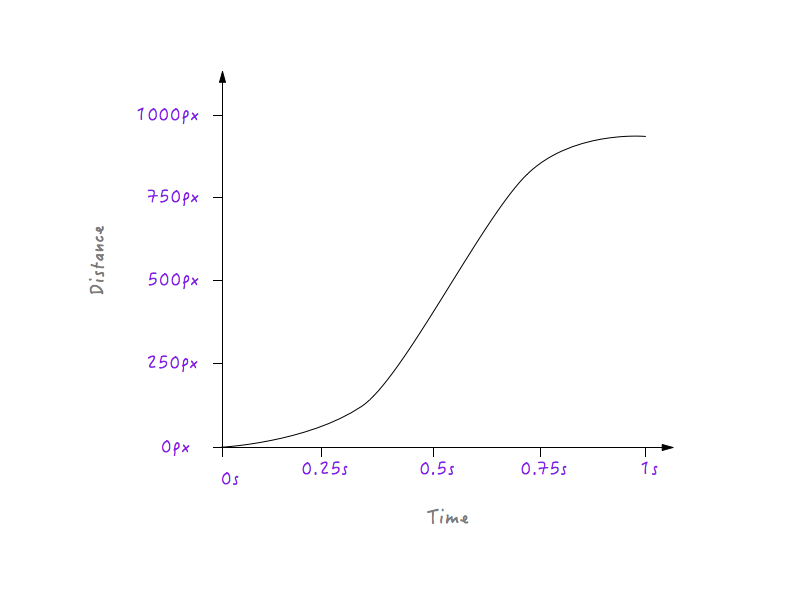
Schau dir Boxy go an! Viel natürlicher, oder?

Die Kurve, die wir anstelle der Ecke gezeichnet haben, ist eigentlich eine Ansammlung vieler kleiner Liniensegmente; und wie Sie bereits wissen, gilt: je steiler die Linie im Diagramm, desto höher die Geschwindigkeit, und je flacher die Linie, desto langsamer die Geschwindigkeit. Beachten Sie, wie im linken Teil des Bildes die Liniensegmente, aus denen die Kurve besteht, steiler und steiler werden, was zu einer allmählichen Erhöhung der Geschwindigkeit führt, und auf der rechten Seite zunehmend flacher werden, was dazu führt, dass die Geschwindigkeit zunehmend abnimmt.

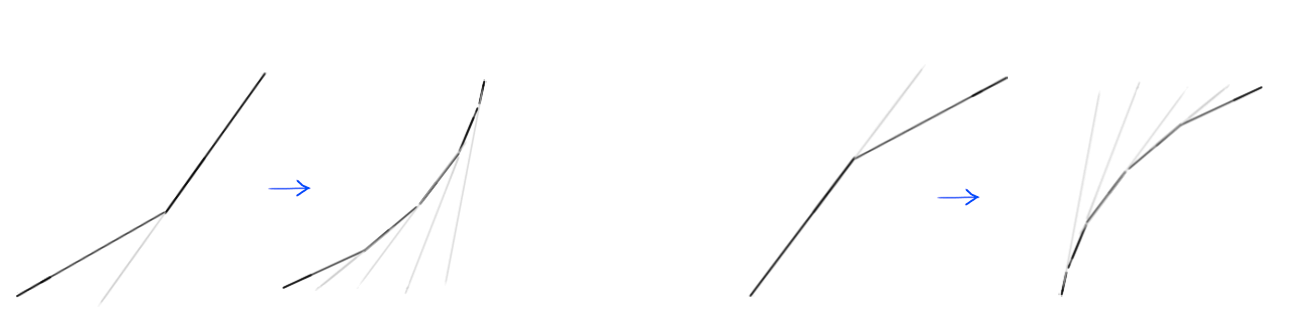
Mit all diesem Wissen wird es viel einfacher, Bewegungskurven zu verstehen. Schauen wir uns ein paar Beispiele an.

Verwenden von Bewegungskurven in der UI-Animation

Wenn Sie das nächste Mal ein UI-Element animieren müssen, steht Ihnen die Kraft der Bewegungskurven zur Verfügung. Ob es sich um eine Slide-out-Leiste, ein modales Fenster oder ein Dropdown-Menü handelt, das Hinzufügen der richtigen Menge an Animationen und das reibungslose und natürliche Aussehen wird die Qualität Ihrer Benutzeroberfläche erheblich verbessern. Dadurch fühlt sich die Benutzeroberfläche einfach gut an. Nehmen Sie das Slideout-Menü unten:

Ein Klick auf das Hamburger-Menü bringt das Menü von links, aber die Animation fühlt sich blockig an. Zeile 51 des CSS zeigt, dass die transition-timing-function der Animation auf linear eingestellt ist. Das können wir verbessern. Lassen Sie uns zu Kubik-Bezier übergehen und eine benutzerdefinierte Timing-Funktion erstellen.

Wenn Sie dies lesen, können Sie davon ausgehen, dass Sie Designer oder Entwickler oder beides sind und daher kubische Bezierkurven nicht fremd sind. Es besteht eine gute Chance, dass Sie ihnen mindestens einmal begegnet sind. Bezier-Kurven sind ein Wunder. Sie werden hauptsächlich in der Computergrafik zum Zeichnen von Formen und in Tools wie Sketch und Adobe Illustrator zum Zeichnen von Vektorgrafiken verwendet. Der Grund, warum kubische Bezierkurven so beliebt sind, ist, dass sie so einfach zu verwenden sind: Ändern Sie einfach die Positionen der vier verschiedenen Punkte und erstellen Sie die Art von Kurve, die Sie benötigen.

Da wir immer den Anfangs- und Endzustand des animierten Objekts kennen, können wir zwei der Punkte fixieren. Damit bleiben nur noch zwei Punkte, deren Positionen wir ändern müssen. Die beiden festen Punkte werden als Ankerpunkte bezeichnet, und die verbleibenden zwei sind Kontrollpunkte.

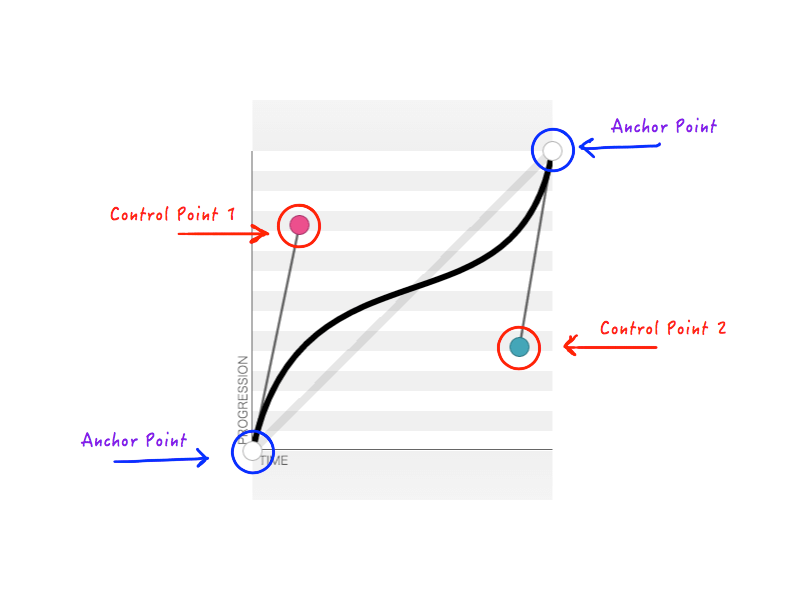
Wie Sie sich erinnern, akzeptiert cubic-bezier vier Zahlen ( n1, n2, n3, n4 ), wenn Sie eine benutzerdefinierte transition-timing-function erstellen. Diese vier Zahlen stellen nichts als die Positionen der beiden Kontrollpunkte dar: n1, n2 stellen die x- und y-Koordinaten des ersten Kontrollpunkts dar, und n3, n4 repräsentieren die Koordinaten des zweiten Kontrollpunkts. Da das Ändern der Position der Kontrollpunkte die Form der Kurve und damit unsere Animation insgesamt ändert, ist das Ergebnis das gleiche, wenn einige oder alle von n1, n2, n3, n4 geändert werden. 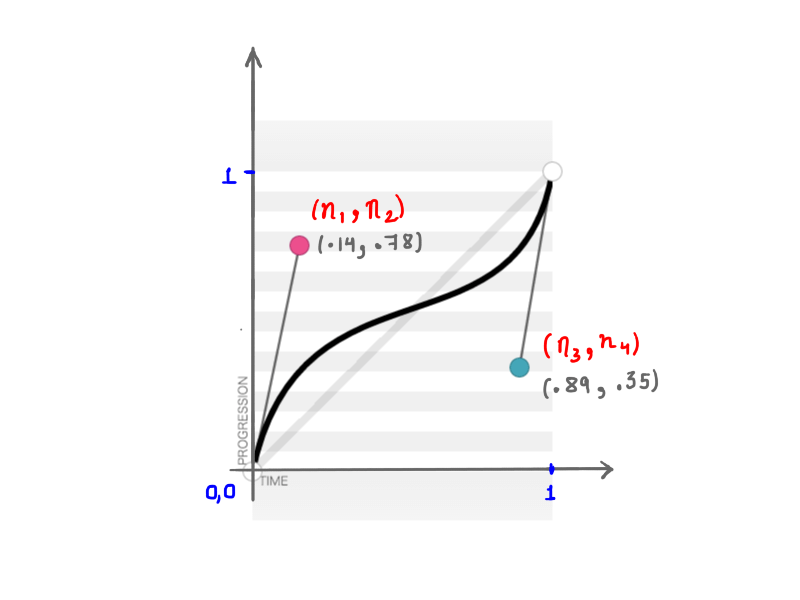Die folgende Abbildung stellt beispielsweise cubic-bezier(.14, .78, .89, .35) :

Die Mathematik hinter diesen scheinbar einfachen Kurven ist faszinierend.

In Ordnung, in Ordnung, lasst uns dahin zurückkehren, wo wir mit Kubik-Bezier hinwollten: Erstellen einer benutzerdefinierten transition-timing-function . Ich möchte die Art von Animation, bei der das Menü sehr schnell hineingleitet und dann elegant langsamer wird und endet:

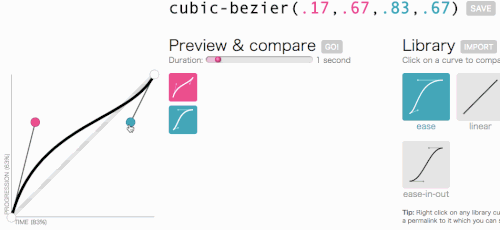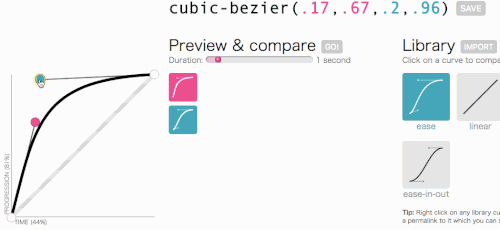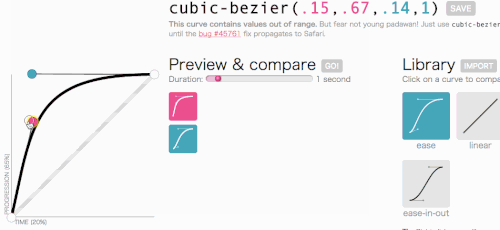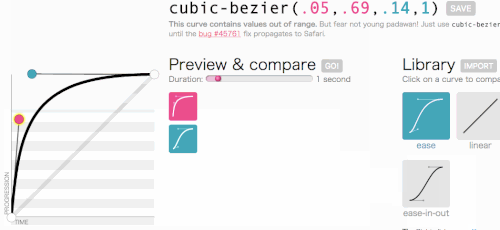
Das sieht gut aus. Die Animation beginnt schnell und verlangsamt sich dann, anstatt sich durchgehend mit konstanter Geschwindigkeit zu bewegen. Ich werde einfach cubic-bezier(.05, .69, .14, 1) vom oberen Rand der Seite kopieren und linear damit ersetzen.

Sieh den Unterschied? Die zweite Iteration fühlt sich viel natürlicher und ansprechender an. Stellen Sie sich vor, jede Animation in Ihrer Benutzeroberfläche folgt einer natürlichen Timing-Funktion. Wie toll wäre das?

Wie wir gesehen haben, sind Bewegungskurven überhaupt nicht schwierig. Sie sind sehr einfach zu verstehen und zu verwenden. Mit ihnen können Sie Ihre Benutzeroberfläche auf die nächste Stufe bringen.

Ich hoffe, Sie haben gelernt, wie Bewegungskurven funktionieren. Wenn Sie viele Versuche und Irrtümer durchlaufen haben, um Bewegungskurven so zu gestalten, wie Sie es möchten, oder wenn Sie sie überhaupt nicht verwendet haben, sollten Sie sie jetzt bequem nach Ihren Wünschen biegen und schöne Animationen erstellen können. Denn schließlich zählt Animation.