Ableitung der Kettenregel beim maschinellen Lernen: Erklärt

Maschinelles Lernen hat sich in den letzten Jahren zu einem der am meisten diskutierten und erforschten Bereiche entwickelt, und das aus all den guten Gründen. Jeden Tag werden neue Modelle und Anwendungen des maschinellen Lernens entdeckt, und Forscher auf der ganzen Welt arbeiten am nächsten großen Ding.

Infolgedessen ist das Interesse von Fachleuten mit unterschiedlichem Hintergrund gestiegen, auf maschinelles Lernen umzusteigen und Teil dieser anhaltenden Revolution zu sein. Wenn Sie ein solcher Enthusiast des maschinellen Lernens sind, der seine ersten Schritte unternehmen möchte, lassen Sie uns Ihnen sagen, dass es vor allem anderen damit beginnt, die Grundlagen der Mathematik und Statistik zu verstehen.

Ein solches wichtiges Thema in der Mathematik, das für maschinelles Lernen von hoher Relevanz ist, sind Ableitungen. Aufgrund Ihres grundlegenden Verständnisses der Analysis würden Sie sich daran erinnern, dass die Ableitung jeder Funktion die momentane Änderungsrate dieser Funktion ist. In diesem Blog tauchen wir tiefer in Derivate ein und untersuchen die Kettenregel. Wir werden sehen, wie sich die Ausgabe einer bestimmten Funktion ändert, wenn wir einige unabhängige Variablen in der Gleichung ändern. Mit dem Wissen über Kettenregelderivate können Sie an der Differenzierung komplexerer Funktionen arbeiten, denen Sie beim maschinellen Lernen mit Sicherheit begegnen werden.

Holen Sie sich die Machine Learning-Zertifizierung online von den besten Universitäten der Welt – Master, Executive Post Graduate Programs und Advanced Certificate Program in ML & AI, um Ihre Karriere zu beschleunigen.

Die Ableitung der Kettenregel verstehen

Die Kettenregel ist im Wesentlichen eine mathematische Formel, mit der Sie die Ableitung einer zusammengesetzten Funktion berechnen können. Eine zusammengesetzte Funktion ist eine, die aus zwei oder mehr Funktionen zusammengesetzt ist. Wenn also f und g zwei Funktionen sind, dann würde uns die Kettenregel helfen, die Ableitung von zusammengesetzten Funktionen wie Nebel oder go f zu finden.

In Anbetracht der zusammengesetzten Funktion fog würde die Ableitung der Kettenregel so aussehen:

Die obige Regel kann auch geschrieben werden als:

Wobei die Funktion F die Zusammensetzung von f und g in Form von f(g(x)) ist.

Angenommen, wir haben drei Variablen, sodass die dritte Variable (z) von der zweiten Variablen (y) abhängt, die wiederum von der ersten Variablen (x) abhängt. In diesem Fall würde die Kettenregelableitung etwa so aussehen:

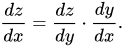In Bezug auf Deep Learning ist dies auch die Formel, die regelmäßig verwendet wird, um Backpropagation-Probleme zu lösen. Da wir nun erwähnt haben, dass z von y und y von x abhängt, können wir z = f(y) und y = g(x) schreiben. Diese Substitution würde unsere Differentialgleichung wie folgt modifizieren:

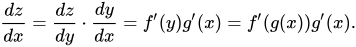Schauen wir uns nun einige Beispiele für Kettenregelderivate an, um die Mathematik dahinter besser zu verstehen.

Beispiele und Anwendungen von Kettenregelderivaten

Nehmen wir ein bekanntes Beispiel aus Wikipedia, um die Kettenregelableitung besser zu verstehen. Angenommen, Sie nehmen einen freien Fall vom Himmel. Der atmosphärische Druck, dem Sie im Herbst begegnen, ändert sich ständig. Hier ist ein Diagramm, das diese Änderung des atmosphärischen Drucks mit Höhenstufen darstellt:

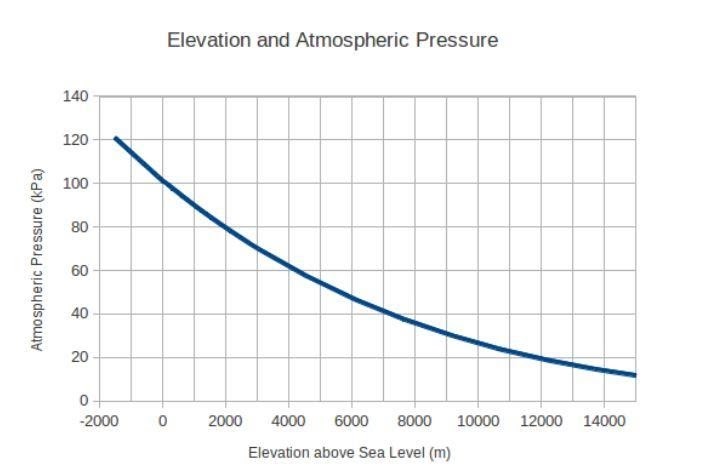
Angenommen, Ihr Sturz begann auf 4000 Metern über dem Meeresspiegel. Anfangs war Ihre Geschwindigkeit Null und der Beschleunigungswert aufgrund der Schwerkraft 9,8 Meter pro Sekunde im Quadrat.

Vergleichen wir nun diese Situation mit der vorherigen Kettenregelmethode. In diesem Beispiel verwenden wir die Variable „t“ für die Zeit anstelle von x.

Dann kann die Variable y = g(t), die die seit Beginn des Sturzes zurückgelegte Strecke angibt, wie folgt angegeben werden:

g(t) = 0,5*9,8t^2

Und die Höhe über dem Meeresspiegel kann durch eine Variable „h“ angegeben werden, die 400-g(t) entspricht.

Nehmen wir an, dass wir aufgrund eines Modells die Funktion des atmosphärischen Drucks in jeder Höhe h auch schreiben können als:

f(h) = 101325 e−0,0001h

Jetzt können Sie zwischen den beiden Gleichungen basierend auf ihren abhängigen Variablen unterscheiden, um die folgenden Ergebnisse zu erhalten:

g'(t) = -9,8 t,

Hier gibt g'(t) den Wert Ihrer Geschwindigkeit zu jedem Zeitpunkt t an.

f'(h) = −10,1325e−0,0001h

Dabei ist f′(h) die Änderungsrate des atmosphärischen Drucks in Bezug auf die Höhe h. Nun stellt sich die Frage, können wir diese beiden Gleichungen kombinieren und die Änderungsrate des Atmosphärendrucks im Laufe der Zeit ableiten? Sehen wir uns die Kettenregel an:

Die letzte Gleichung, die wir haben, liefert uns die Änderungsrate des atmosphärischen Drucks in Bezug auf die seit dem Herbst vergangene Zeit. In Bezug auf maschinelles Lernen benötigen neuronale Netze ständig Gewichtsaktualisierungen bezüglich des Vorhersagefehlers des Neurons. Die Kettenregel hilft dabei, diese Gewichtungen anzupassen und das maschinelle Lernmodell näher an die korrekte Ausgabe zu bringen.

Fazit

Wie Sie sehen können, ist die Kettenregel für viele Zwecke von Vorteil. Besonders beim maschinellen Lernen oder Deep Learning findet die Kettenregel viel Verwendung, um die Gewichte der Neuronen zu aktualisieren und die Gesamteffizienz des Modells zu verbessern.

Nun, da Sie sich der Grundlagen der Kettenregel bewusst sind, können Sie selbst ein paar Probleme lösen. Suchen Sie ein paar zusammengesetzte Funktionen und versuchen Sie, ihre Ableitungen zu finden. Je mehr Sie üben, desto klarer werden Ihre Konzepte und desto einfacher wird es für Sie, Ihre Modelle für maschinelles Lernen zu trainieren! Das heißt, wenn Sie ein Enthusiast für maschinelles Lernen sind, aber Schwierigkeiten haben, Ihre ersten Schritte in diesem Bereich zu unternehmen, unterstützt upGrad Ihren Rücken!

Unser Executive PG Program in Machine Learning & AI wird in Zusammenarbeit mit IIIT-Bangalore angeboten und bietet Ihnen die Wahl zwischen sechs branchenrelevanten Spezialisierungen. Der Kurs beginnt am Boden und führt Sie zum Höhepunkt, während er Ihnen 1-zu-1-Unterstützung durch Branchenexperten, eine starke Gruppe von Studenten und eine 360-Grad-Karriereunterstützung bietet.