Bayessche Statistik und Modell: Erklärt

Die Bayes'sche Technik ist ein Ansatz in der Statistik, der bei der Datenanalyse und Parameterschätzung verwendet wird. Dieser Ansatz basiert auf dem Satz von Bayes.

Bayes'sche Statistik folgt einem einzigartigen Prinzip, bei dem es hilft, die gemeinsame Wahrscheinlichkeitsverteilung für beobachtete und nicht beobachtete Parameter unter Verwendung eines statistischen Modells zu bestimmen. Die Kenntnis der Statistik ist unerlässlich, um analytische Probleme in diesem Szenario anzugehen.

Seit der Einführung des Bayes-Theorems in den 1770er Jahren durch Thomas Bayes ist es ein unverzichtbares Werkzeug in der Statistik geblieben. Bayes'sche Modelle sind ein klassischer Ersatz für frequentistische Modelle, da jüngste Innovationen in der Statistik dazu beigetragen haben, Meilensteine ​​in einer Vielzahl von Branchen zu überschreiten, darunter die medizinische Forschung, das Verständnis von Websuchen und die Verarbeitung natürlicher Sprachen (Natural Language Processing).

Beispielsweise ist Alzheimer eine Krankheit, von der bekannt ist, dass sie mit zunehmendem Alter ein zunehmendes Risiko darstellt. Mit Hilfe des Bayes-Theorems können Ärzte jedoch die Wahrscheinlichkeit abschätzen, dass eine Person in Zukunft an Alzheimer erkrankt. Dies gilt auch für Krebs und andere altersbedingte Krankheiten, für die eine Person in den späteren Jahren ihres Lebens anfällig wird.

Häufige Statistiken vs. Bayes'sche Statistik

Frequent Statistics vs. Bayes'sche Statistik war immer wieder ein Thema von Kontroversen und Albträumen für Anfänger, die beide Schwierigkeiten haben, sich zwischen den beiden zu entscheiden. Zu Beginn des 20. Jahrhunderts war die Bayes'sche Statistik mit Misstrauens- und Akzeptanzproblemen konfrontiert. Mit der Zeit erkannten die Menschen jedoch die Anwendbarkeit von Bayes'schen Modellen und die genauen Lösungen, die sie liefern.

Hier ist ein Blick auf häufige Statistiken und die damit verbundene Komplexität:

Häufige Statistiken

Es ist eine weit verbreitete Inferenzmethode in der Welt der Statistik. Es analysiert, ob ein Ereignis (als Hypothese erwähnt) stattgefunden hat oder nicht. Es schätzt auch die Wahrscheinlichkeit, dass das Ereignis während der Spanne des Experiments auftritt. Das Experiment wird wiederholt, bis das gewünschte Ergebnis erreicht ist.

Ihre Verteilungsstichproben haben die tatsächliche Größe, und das Experiment wird theoretisch unendlich oft wiederholt. Hier ist ein Beispiel, das zeigt, wie häufig Statistiken verwendet werden können, um das Werfen einer Münze zu untersuchen.

• Die Wahrscheinlichkeit, beim einmaligen Werfen der Münze Kopf zu bekommen, beträgt 0,5 (1/2).
• Die Anzahl der Köpfe gibt die tatsächliche Anzahl der erhaltenen Leads an.
• Die Differenz zwischen der tatsächlichen Kopfzahl und der erwarteten Kopfzahl wird größer, wenn die Anzahl der Würfe zunimmt.

Hier hängt das Ergebnis also davon ab, wie oft das Experiment wiederholt wird. Dies ist ein großer Nachteil häufiger Statistiken.

Andere Mängel im Zusammenhang mit seinen Konstruktions- und Interpretationstechniken wurden im 20. Jahrhundert offensichtlich, als die Anwendung häufiger Statistiken auf numerische Modelle ihren Höhepunkt erreichte.

Einschränkungen der häufigen Statistik

Die drei Hauptfehler häufiger Statistiken sind unten aufgeführt:

1. Variable p-Werte

Die für eine Stichprobe mit fester Größe in einem Experiment mit definiertem Endpunkt gemessenen Werte von p ändern sich mit jeder Änderung des Endpunkts und der Stichprobengröße. Dies führt zu zwei p-Werten für einzelne Daten, was falsch ist.

2. Inkonsistente Konfidenzintervalle

CI (Konfidenzintervall) hängt ausschließlich von der Stichprobengröße ab. Es macht das Stopppotential irrelevant.

3. Geschätzte Werte von CI

Konfidenzintervalle sind keine Wahrscheinlichkeitsverteilung, und ihre Werte für einen Parameter sind nur eine Schätzung und keine tatsächlichen Werte.

Aus den drei oben genannten Gründen entstand der Bayes'sche Ansatz, der Wahrscheinlichkeiten auf statistische Probleme anwendet.

Geburt der Bayesschen Statistik

Reverend Thomas Bayes schlug erstmals in seinem Aufsatz aus dem Jahr 1763 den Bayes'schen Ansatz für die Statistik vor. Dieser Ansatz wurde von Richard Price als Strategie in umgekehrter Wahrscheinlichkeit veröffentlicht, um zukünftige Ereignisse auf der Grundlage der Vergangenheit vorherzusagen.

Der Ansatz basiert auf dem Bayes-Theorem, das im Folgenden erläutert wird:

Satz von Bayes

Renyis Wahrscheinlichkeitsaxiom untersucht bedingte Wahrscheinlichkeiten, wobei die Möglichkeiten des Eintretens von Ereignis A und Ereignis B abhängig oder bedingt sind. Die grundlegende bedingte Wahrscheinlichkeit kann geschrieben werden als:

Die Wahrscheinlichkeit, dass Ereignis B eintritt, hängt von Ereignis A ab.

Die obige Gleichung ist die Grundlage der Bayes-Regel, einem mathematischen Ausdruck des Bayes-Theorems, das besagt:

Hier bedeutet ∩ Schnittpunkt.

Die Bayes-Regel kann geschrieben werden als:

Die Bayes-Regel ist die Grundlage der Bayesschen Statistik, bei der die verfügbaren Informationen zu einem bestimmten Parameter in einem statistischen Modell mit gesammelten Daten verglichen und aktualisiert werden.

Das Hintergrundwissen wird als vorherige Verteilung dargestellt, die dann mit den beobachteten oder gesammelten Daten als Wahrscheinlichkeitsfunktion verglichen und untersucht wird, um die spätere Verteilung herauszufinden.

Diese spätere Verteilung wird verwendet, um Vorhersagen über zukünftige Ereignisse zu treffen.

Anwendungen des Bayes'schen Ansatzes hängen von folgenden Parametern ab:

1. Definieren des Prior- und Datenmodells
2. Relevante Schlussfolgerungen ziehen
3. Überprüfung und Optimierung der Modelle

Was sind Bayes'sche neuronale Netze?

Bayes'sche neuronale Netze (BNNs) sind Netze, die Sie erstellen, wenn Sie Standardnetze mithilfe der statistischen Methodik erweitern und die nachträgliche Inferenz ändern, um eine Überanpassung zu verfolgen. Da es sich um einen Bayes'schen Ansatz handelt, gibt es eine Wahrscheinlichkeitsverteilung, die den Parametern der neuronalen Netze zugeordnet ist.

Sie werden verwendet, um komplexe Probleme zu lösen, bei denen kein freier Datenfluss verfügbar ist. Bayessche neuronale Netze helfen, die Überanpassung in Bereichen wie Molekularbiologie und medizinische Diagnose zu kontrollieren.

Mit Bayes'schen neuronalen Netzen kann man eine ganze Verteilung von Antworten auf eine Frage in Betracht ziehen und nicht nur eine Möglichkeit. Sie helfen Ihnen, die Modellauswahl/den Modellvergleich zu bestimmen und Probleme anzugehen, die eine Regularisierung beinhalten.

Bayessche Statistik bietet mathematische Werkzeuge, um subjektives Wissen über neue Daten oder wissenschaftliche Beweise zu rationalisieren und zu aktualisieren. Im Gegensatz zum häufigen statistischen Ansatz funktioniert es auf der Annahme, dass Wahrscheinlichkeiten von der Häufigkeit von Ereignissen abhängen, die sich unter denselben Bedingungen wiederholen.

Kurz gesagt, die Bayes'sche Technik ist eine Erweiterung der Annahme und Meinung eines Individuums. Der Schlüsselaspekt des Bayes'schen Modells, der es effizienter macht, ist sein Verständnis, dass Einzelpersonen in ihren Meinungen basierend auf der Art der Informationen, die sie erhalten, unterschiedlich sind.

Wenn jedoch neue Beweise und Daten auftauchen, haben die Individuen einen Konvergenzpunkt, die Bayes'sche Inferenz . Diese rationale Aktualisierung ist das besondere Merkmal der Bayes'schen Statistik, das sie bei analytischen Problemen effektiver macht.

Hier wird die Wahrscheinlichkeit 0 angewendet, wenn keine Hoffnung auf das Eintreten eines Ereignisses besteht, und die Wahrscheinlichkeit 1 wird angewendet, wenn es sicher ist, dass das Ereignis eintritt. Eine Wahrscheinlichkeit zwischen 0 und 1 gibt Raum für andere mögliche Ergebnisse.

Die Bayes-Regel wird nun angewendet, um eine bayessche Inferenz zu erreichen und eine bessere Inferenz aus dem Modell zu erhalten.

Wie wenden Sie die Bayes-Regel an, um die Bayes'sche Inferenz zu erhalten?

Betrachten Sie die Gleichung:

P(θ|D) = P(D|θ.)P(θ) / P(D)

P(θ) bezeichnet die vorherige Verteilung,

P(θ|D) bezeichnet den späteren Glauben,

P(D) stellt den Beweis dar,

P(D|θ) gibt die Wahrscheinlichkeit an.

Das Hauptziel der bayesschen Inferenz besteht darin, eine rationale und mathematisch genaue Methode zum Mischen der Überzeugungen mit Beweisen anzubieten, um aktualisierte spätere Überzeugungen zu erhalten. Die späteren Annahmen können als vorherige Annahmen verwendet werden, wenn neue Daten generiert werden. Somit hilft die Bayes'sche Inferenz, Überzeugungen mit Hilfe der Bayes'schen Regel kontinuierlich zu aktualisieren.

Betrachtet man das gleiche Münzwurfbeispiel, so aktualisiert das Bayes'sche Modell die Prozedur von vorher zu späterer Überzeugung mit neuen Münzwürfen. Das Bayes'sche Verfahren ergibt die folgenden Wahrscheinlichkeiten.

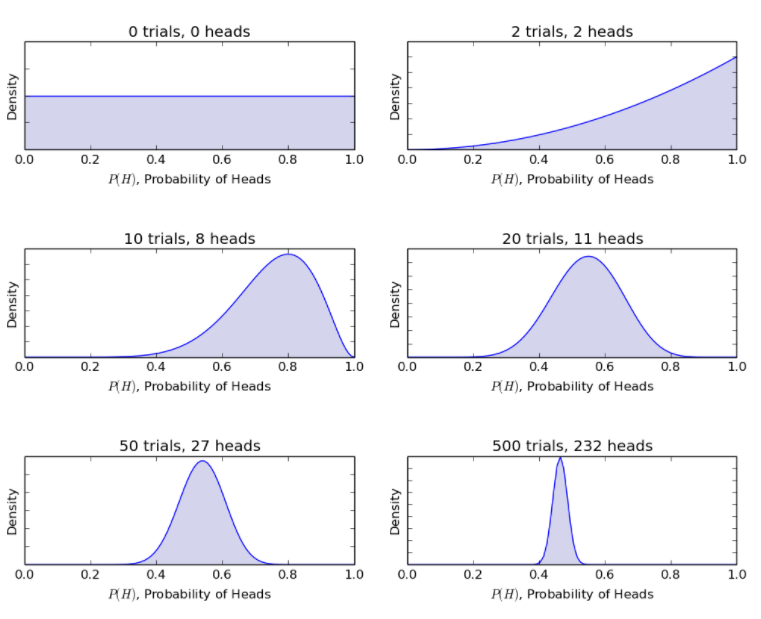
Quelle

Somit ermöglicht das Bayes'sche Modell die Rationalisierung eines unsicheren Szenarios mit eingeschränkten Informationen zu einem genauer definierten Szenario mit einer beträchtlichen Datenmenge.

Bemerkenswerte Unterschiede zwischen dem Bayes'schen Modell und dem Frequentistenmodell

Häufige Statistiken

Bayessche Statistik

Das Ziel wird als Punktschätzung und CI betrachtet

Das Ziel wird als spätere Verteilung betrachtet

Das Verfahren beginnt mit den Beobachtungen

Der Prozess beginnt mit der vorherigen Verteilung

Immer wenn neue Beobachtungen gemacht werden, berechnet der frequentistische Ansatz das bestehende Modell neu.

Immer wenn neue Beobachtungen gemacht werden, wird die Posterior-Verteilung (Ideologie/Hypothese) aktualisiert

Beispiele: Schätzung des Mittelwerts, t-Test und ANOVA.

Beispiele: Schätzung der A-posteriori-Verteilung von Mittelwert und Überlappung von Intervallen mit hoher Dichte.

Vorteile der Bayesschen Statistik

• Es bietet ein organisches und einfaches Mittel, um vorgefasste Informationen mit einem soliden Rahmen und wissenschaftlichen Erkenntnissen zu verbinden. Die vergangenen Informationen über einen Parameter können verwendet werden, um eine vorherige Verteilung für zukünftige Untersuchungen zu bilden. Die Schlüsse folgen dem Satz von Bayes.
• Die Schlussfolgerungen aus einem Bayes'schen Modell sind logisch und mathematisch genau und keine groben Annahmen. Die Genauigkeit bleibt unabhängig von der Größe der Probe konstant.
• Bayessche Statistik folgt dem Likelihood-Prinzip. Wenn zwei unterschiedliche Stichproben eine gemeinsame Wahrscheinlichkeitsfunktion für eine Überzeugung θ haben, sollten alle Rückschlüsse auf die Überzeugung ähnlich sein. Klassische statistische Verfahren folgen nicht dem Likelihood-Prinzip.
• Die Lösungen aus einer Bayes'schen Analyse können leicht interpretiert werden.
• Es bietet eine förderliche Plattform für verschiedene Modelle wie hierarchische Modelle und Probleme mit unvollständigen Daten. Die Berechnungen aller parametrischen Modelle können mit Hilfe anderer numerischer Verfahren virtuell nachvollzogen werden.

Erfolgreiche Anwendungen Bayes'scher Modelle im Laufe der Geschichte

Bayesianische Methoden hatten viele erfolgreiche Anwendungen während des Zweiten Weltkriegs. Einige davon sind unten aufgeführt:

• Ein russischer Statistiker, Andrey Kolmogorov , verwendete erfolgreich bayessche Methoden, um die Effizienz der russischen Artillerie zu verbessern.
• Bayes'sche Modelle wurden verwendet, um die Codes deutscher U-Boote zu knacken.
• Ein in Frankreich geborener amerikanischer Mathematiker, Bernard Koopman, half den Verbündeten, die Position deutscher U-Boote mit Hilfe von Bayes'schen Modellen zu identifizieren, um die Funkübertragungen abzufangen.

Wenn Sie mehr über Bayes'sche Statistik erfahren möchten, finden Sie hier die fortgeschrittene Zertifizierung von upGrad für maschinelles Lernen und Cloud , um die zugrunde liegenden Konzepte anhand realer Branchenprojekte und Fallstudien zu verstehen. Der 12-monatige Kurs wird vom IIT Madras angeboten und unterstützt das Lernen im eigenen Tempo.

Kontaktieren Sie uns für weitere Details.