Beispiel für ein Bayes'sches Netzwerk [mit grafischer Darstellung]

Einführung

In der Statistik werden probabilistische Modelle verwendet, um eine Beziehung zwischen Variablen zu definieren, und können verwendet werden, um die Wahrscheinlichkeiten jeder Variablen zu berechnen. Bei vielen Problemen gibt es eine große Anzahl von Variablen. In solchen Fällen erfordern die vollständig bedingten Modelle eine riesige Datenmenge, um jeden einzelnen Fall der Wahrscheinlichkeitsfunktionen abzudecken, deren Berechnung in Echtzeit schwierig sein kann. Es gab mehrere Versuche, die bedingten Wahrscheinlichkeitsberechnungen wie Naive Bayes zu vereinfachen, aber es erweist sich dennoch als nicht effizient, da es mehrere Variablen drastisch reduziert.

Die einzige Möglichkeit besteht darin, ein Modell zu entwickeln, das die bedingten Abhängigkeiten zwischen Zufallsvariablen und die bedingte Unabhängigkeit in anderen Fällen bewahren kann. Dies führt uns zum Konzept der Bayes'schen Netze. Diese Bayes'schen Netzwerke helfen uns, das probabilistische Modell für jede Domäne effektiv zu visualisieren und die Beziehung zwischen Zufallsvariablen in Form eines benutzerfreundlichen Diagramms zu untersuchen.

Lernen Sie ML-Kurse von den besten Universitäten der Welt. Erwerben Sie Master-, Executive PGP- oder Advanced Certificate-Programme, um Ihre Karriere zu beschleunigen.

Was sind Bayes'sche Netzwerke?

Per Definition sind Bayes-Netzwerke eine Art probabilistisches grafisches Modell, das die Bayes-Inferenzen für Wahrscheinlichkeitsberechnungen verwendet. Es stellt eine Reihe von Variablen und ihre bedingten Wahrscheinlichkeiten mit einem gerichteten azyklischen Graphen (DAG) dar. Sie eignen sich in erster Linie dazu, ein eingetretenes Ereignis zu berücksichtigen und die Wahrscheinlichkeit vorherzusagen, dass eine der mehreren möglichen bekannten Ursachen der beitragende Faktor ist.

Quelle

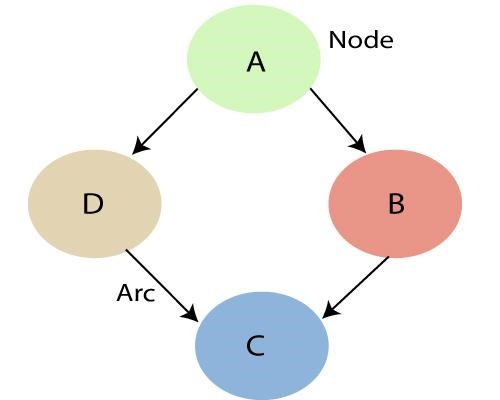
Wie oben erwähnt, können wir durch Verwendung der Beziehungen, die durch das Bayes'sche Netzwerk spezifiziert sind, die Joint Probability Distribution (JPF) mit den bedingten Wahrscheinlichkeiten erhalten. Jeder Knoten im Diagramm stellt eine Zufallsvariable dar und der Bogen (oder gerichtete Pfeil) stellt die Beziehung zwischen den Knoten dar. Sie können entweder kontinuierlicher oder diskreter Natur sein.

Im obigen Diagramm sind A, B, C und D 4 Zufallsvariablen, die durch Knoten dargestellt werden, die im Netzwerk des Diagramms angegeben sind. Für Knoten B ist A sein übergeordneter Knoten und C sein untergeordneter Knoten. Knoten C ist unabhängig von Knoten A.

Bevor wir uns mit der Implementierung eines Bayes'schen Netzwerks befassen, müssen einige Wahrscheinlichkeitsgrundlagen verstanden werden.

Lokales Markov-Grundstück

Die Bayes'schen Netzwerke erfüllen die Eigenschaft, die als lokale Markov-Eigenschaft bekannt ist. Es besagt, dass ein Knoten aufgrund seiner Eltern bedingt unabhängig von seinen Nicht-Nachkommen ist. Im obigen Beispiel ist P(D|A, B) gleich P(D|A), da D unabhängig von seinem Nicht-Nachkommen B ist. Diese Eigenschaft hilft uns bei der Vereinfachung der gemeinsamen Verteilung. Die lokale Markov-Eigenschaft führt uns zum Konzept eines Markov-Zufallsfelds, bei dem es sich um ein zufälliges Feld um eine Variable handelt, von der gesagt wird, dass sie Markov-Eigenschaften folgt.

Bedingte Wahrscheinlichkeit

In der Mathematik ist die bedingte Wahrscheinlichkeit von Ereignis A die Wahrscheinlichkeit, dass Ereignis A eintritt, wenn bereits ein anderes Ereignis B eingetreten ist. Einfach ausgedrückt ist p(A | B) die Wahrscheinlichkeit, dass Ereignis A eintritt, vorausgesetzt, dass Ereignis B eintritt. Es gibt jedoch zwei Arten von Ereignismöglichkeiten zwischen A und B. Sie können entweder abhängige Ereignisse oder unabhängige Ereignisse sein. Abhängig von ihrem Typ gibt es zwei verschiedene Möglichkeiten, die bedingte Wahrscheinlichkeit zu berechnen.

• Da A und B abhängige Ereignisse sind, wird die bedingte Wahrscheinlichkeit wie folgt berechnet: P (A | B) = P (A und B) / P (B)
• Wenn A und B unabhängige Ereignisse sind, dann ist der Ausdruck für die bedingte Wahrscheinlichkeit gegeben durch: P(A|B) = P(A)

Gemeinsame Wahrscheinlichkeitsverteilung

Bevor wir uns mit einem Beispiel für Bayes'sche Netzwerke befassen, lassen Sie uns das Konzept der gemeinsamen Wahrscheinlichkeitsverteilung verstehen. Betrachten Sie 3 Variablen a1, a2 und a3. Per Definition werden die Wahrscheinlichkeiten aller verschiedenen möglichen Kombinationen von a1, a2 und a3 als gemeinsame Wahrscheinlichkeitsverteilung bezeichnet.

Wenn P[a1,a2, a3,….., an] die JPD der folgenden Variablen von a1 bis an ist, dann gibt es mehrere Möglichkeiten, die gemeinsame Wahrscheinlichkeitsverteilung als Kombination verschiedener Begriffe zu berechnen, wie z.

P[a1,a2, a3,….., an] = P[a1 | a2, a3,….., an] * P[a2, a3,….., an]

= P[a1 | a2, a3,….., an] * P[a2 | a3,….., an]….P[an-1|an] * P[an]

Wenn wir die obige Gleichung verallgemeinern, können wir die gemeinsame Wahrscheinlichkeitsverteilung schreiben als

P(X i |X i-1 ,………, X n ) = P(X i |Eltern(X i ))

Beispiel für Bayes'sche Netzwerke

Lassen Sie uns nun den Mechanismus von Bayes'schen Netzen und ihre Vorteile anhand eines einfachen Beispiels verstehen. Stellen wir uns in diesem Beispiel vor, wir hätten die Aufgabe, die Noten ( m ) eines Studenten für eine gerade abgegebene Prüfung zu modellieren. Aus dem gegebenen Bayes'schen Netzwerkdiagramm unten sehen wir, dass die Markierungen von zwei anderen Variablen abhängen. Sie sind,

• Prüfungsstufe ( e )– Diese diskrete Variable gibt die Schwierigkeit der Prüfung an und hat zwei Werte (0 für einfach und 1 für schwierig)
• IQ-Level ( i ) – Dies stellt den Intelligenzquotienten des Schülers dar und ist ebenfalls diskreter Natur mit zwei Werten (0 für niedrig und 1 für hoch)

Darüber hinaus führt uns das IQ-Niveau des Schülers auch zu einer anderen Variablen, nämlich dem Eignungswert des Schülers ( s ). Mit den erzielten Noten kann sich der Student nun die Zulassung an einer bestimmten Universität sichern. Die Wahrscheinlichkeitsverteilung für die Zulassung ( a ) an einer Universität ist ebenfalls unten angegeben.

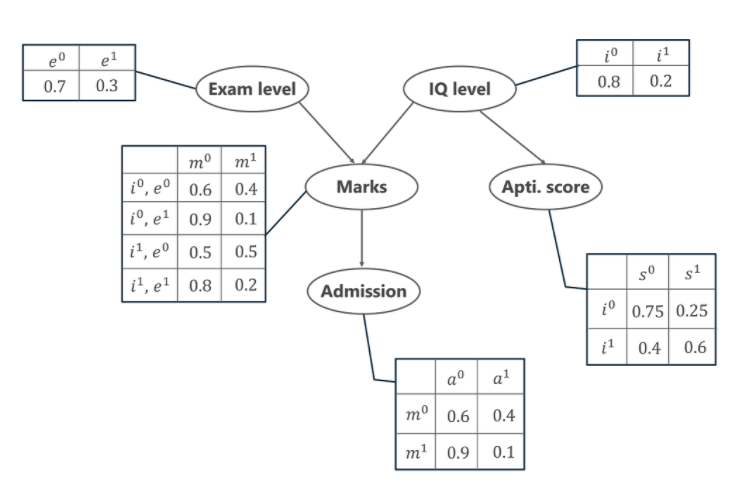
In der obigen Grafik sehen wir mehrere Tabellen, die die Wahrscheinlichkeitsverteilungswerte der gegebenen 5 Variablen darstellen. Diese Tabellen werden als bedingte Wahrscheinlichkeitstabelle oder CPT bezeichnet. Es gibt einige Eigenschaften des CPT, die unten angegeben sind –

• Die Summe der CPT-Werte in jeder Zeile muss gleich 1 sein, da alle möglichen Fälle für eine bestimmte Variable erschöpfend sind (alle Möglichkeiten darstellen).
• Wenn eine Variable, die ihrer Natur nach boolesch ist, k boolesche Eltern hat, dann hat sie im CPT 2K Wahrscheinlichkeitswerte.

Um auf unser Problem zurückzukommen, lassen Sie uns zunächst alle möglichen Ereignisse auflisten, die in der oben angegebenen Tabelle auftreten.

1. Prüfungsstufe (e)
2. IQ-Level (i)
3. Eignungsbewertung (en)
4. Noten (m)
5. Eintritt (a)

Diese fünf Variablen werden in Form eines gerichteten azyklischen Graphen (DAG) in einem Bayes'schen Netzwerkformat mit ihren bedingten Wahrscheinlichkeitstabellen dargestellt. Um nun die gemeinsame Wahrscheinlichkeitsverteilung der 5 Variablen zu berechnen, ist die Formel gegeben durch:

P[a, m, i, e, s]= P(a | m) . P(m | ich, e) . P(i) . Sport) . P(s | ich)

Aus der obigen Formel

• P(a | m) bezeichnet die bedingte Wahrscheinlichkeit, dass der Student aufgrund seiner Noten in der Prüfung zugelassen wird.
• P(m | i, e) stellt die Noten dar, die der Schüler aufgrund seines IQ-Niveaus und der Schwierigkeit des Prüfungsniveaus erzielen wird.
• P(i) und P(e) stellen die Wahrscheinlichkeit des IQ-Niveaus und des Prüfungs-Niveaus dar.
• P(s | i) ist die bedingte Wahrscheinlichkeit des Eignungswerts des Schülers angesichts seines IQ-Niveaus.

Mit den folgenden berechneten Wahrscheinlichkeiten können wir die gemeinsame Wahrscheinlichkeitsverteilung des gesamten Bayes-Netzwerks finden.

Berechnung der gemeinsamen Wahrscheinlichkeitsverteilung

Lassen Sie uns nun die JPD für zwei Fälle berechnen.

Fall 1: Berechnen Sie die Wahrscheinlichkeit, dass trotz eines schwierigen Prüfungsniveaus der Student mit einem niedrigen IQ-Niveau und einem niedrigen Eignungswert die Prüfung besteht und die Zulassung zur Universität sichert.

Aus der obigen Wortaufgabe lässt sich die gemeinsame Wahrscheinlichkeitsverteilung wie folgt schreiben:

P[a=1, m=1, i=0, e=1, s=0]

Aus den obigen Tabellen für bedingte Wahrscheinlichkeiten werden die Werte für die gegebenen Bedingungen in die Formel eingespeist und wie folgt berechnet.

P[a=1, m=1, i=0, e=0, s=0] = P(a=1 | m=1) . P(m=1 | i=0, e=1) . P(i=0) . P(e=1) . P(s=0 | i=0)

= 0,1 * 0,1 * 0,8 * 0,3 * 0,75

= 0,0018

Fall 2: Berechnen Sie in einem anderen Fall die Wahrscheinlichkeit, dass der Student ein hohes IQ-Niveau und einen hohen Eignungswert hat, die Prüfung einfach ist, aber nicht bestanden wird und die Zulassung zur Universität nicht sichert.

Die Formel für die JPD ist gegeben durch

P[a=0, m=0, i=1, e=0, s=1]

Daher,

P[a=0, m=0, i=1, e=0, s=1]= P(a=0 | m=0) . P(m=0 | i=1, e=0) . P(i=1) . P(e=0) . P(s=1 | i=1)

= 0,6 * 0,5 * 0,2 * 0,7 * 0,6

= 0,0252

Daher können wir auf diese Weise Bayes'sche Netzwerke und Wahrscheinlichkeitstabellen verwenden, um die Wahrscheinlichkeit für verschiedene mögliche Ereignisse zu berechnen, die auftreten.

Lesen Sie auch: Ideen und Themen für Machine Learning-Projekte

Fazit

Es gibt unzählige Anwendungen für Bayes'sche Netzwerke in der Spam-Filterung, der semantischen Suche, dem Abruf von Informationen und vielem mehr. Beispielsweise können wir mit einem bestimmten Symptom die Wahrscheinlichkeit vorhersagen, dass eine Krankheit auftritt, wobei mehrere andere Faktoren zur Krankheit beitragen. Daher wird in diesem Artikel das Konzept des Bayes'schen Netzwerks zusammen mit seiner Implementierung anhand eines Beispiels aus der Praxis vorgestellt.

Wenn Sie neugierig sind, maschinelles Lernen und KI zu meistern, steigern Sie Ihre Karriere mit einem Fortgeschrittenenkurs für maschinelles Lernen und KI mit IIIT-B und der Liverpool John Moores University.