Bayes-Theorem im maschinellen Lernen: Einführung, Anwendung und Beispiel
Veröffentlicht: 2021-02-04Inhaltsverzeichnis
Einführung: Was ist der Satz von Bayes?
Das Bayes-Theorem ist nach dem englischen Mathematiker Thomas Bayes benannt, der sich intensiv mit der Entscheidungstheorie beschäftigt hat, dem Bereich der Mathematik, der sich mit Wahrscheinlichkeiten befasst. Das Bayes-Theorem wird auch häufig beim maschinellen Lernen verwendet, wo es eine einfache und effektive Möglichkeit darstellt, Klassen mit Präzision und Genauigkeit vorherzusagen. Die Bayes'sche Methode zur Berechnung bedingter Wahrscheinlichkeiten wird in maschinellen Lernanwendungen verwendet, die Klassifizierungsaufgaben beinhalten.
Eine vereinfachte Version des Bayes-Theorems, bekannt als Naive-Bayes-Klassifizierung, wird verwendet, um Rechenzeit und -kosten zu reduzieren. In diesem Artikel führen wir Sie durch diese Konzepte und diskutieren die Anwendungen des Bayes-Theorems beim maschinellen Lernen.
Nehmen Sie online an den Kursen für maschinelles Lernen von den besten Universitäten der Welt teil – Masters, Executive Post Graduate Programs und Advanced Certificate Program in ML & AI, um Ihre Karriere zu beschleunigen.
Warum das Bayes-Theorem beim maschinellen Lernen verwenden?
Das Bayes-Theorem ist eine Methode zur Bestimmung bedingter Wahrscheinlichkeiten – d. h. der Wahrscheinlichkeit, dass ein Ereignis eintritt, wenn bereits ein anderes Ereignis eingetreten ist. Da eine bedingte Wahrscheinlichkeit zusätzliche Bedingungen enthält – mit anderen Worten mehr Daten – kann sie zu genaueren Ergebnissen beitragen.
Daher sind bedingte Wahrscheinlichkeiten ein Muss, um genaue Vorhersagen und Wahrscheinlichkeiten beim maschinellen Lernen zu bestimmen. Da das Feld in einer Vielzahl von Domänen immer allgegenwärtiger wird, ist es wichtig, die Rolle von Algorithmen und Methoden wie dem Bayes-Theorem beim maschinellen Lernen zu verstehen.
Bevor wir auf den Satz selbst eingehen, wollen wir einige Begriffe anhand eines Beispiels verstehen. Angenommen, ein Buchhandlungsleiter hat Informationen über das Alter und das Einkommen seiner Kunden. Er möchte wissen, wie sich die Buchverkäufe auf drei Altersklassen von Kunden verteilen: Jugendliche (18–35), mittleres Alter (35–60) und Senioren (60+).

Nennen wir unsere Daten X. In der Bayes'schen Terminologie wird X Evidenz genannt. Wir haben eine Hypothese H, wo wir ein X haben, das zu einer bestimmten Klasse C gehört.
Unser Ziel ist es, die bedingte Wahrscheinlichkeit unserer Hypothese H bei gegebenem X zu bestimmen, dh P(H | X).
Einfach ausgedrückt erhalten wir durch die Bestimmung von P(H | X) die Wahrscheinlichkeit, dass X zur Klasse C gehört, wenn X gegeben ist. X hat die Attribute Alter und Einkommen – sagen wir zum Beispiel, 26 Jahre alt mit einem Einkommen von 2000 Dollar. H ist unsere Hypothese, dass der Kunde das Buch kaufen wird.
Achten Sie genau auf die folgenden vier Begriffe:
- Beweis – Wie bereits erwähnt, ist P(X) als Beweis bekannt. Es ist einfach die Wahrscheinlichkeit, dass der Kunde in diesem Fall 26 Jahre alt ist und 2000 $ verdient.
- Die Prior-Wahrscheinlichkeit – P(H), bekannt als Prior-Wahrscheinlichkeit, ist die einfache Wahrscheinlichkeit unserer Hypothese – nämlich, dass der Kunde ein Buch kaufen wird. Diese Wahrscheinlichkeit wird nicht mit einer zusätzlichen Eingabe auf der Grundlage von Alter und Einkommen versehen. Da die Berechnung mit weniger Informationen erfolgt, ist das Ergebnis weniger genau.
- Posterior-Wahrscheinlichkeit – P(H | X) ist als Posterior-Wahrscheinlichkeit bekannt. Hier ist P(H | X) die Wahrscheinlichkeit, dass der Kunde ein Buch (H) bei gegebenem X kauft (dass er 26 Jahre alt ist und 2000 $ verdient).
- Wahrscheinlichkeit – P(X | H) ist die Wahrscheinlichkeitswahrscheinlichkeit. Da wir wissen, dass der Kunde das Buch kaufen wird, ist die Likelihood-Wahrscheinlichkeit in diesem Fall die Wahrscheinlichkeit, dass der Kunde 26 Jahre alt ist und ein Einkommen von 2000 $ hat.
Angesichts dessen besagt das Bayes Theorem:
P(H | X) = [ P(X | H) * P(H) ] / P(X)
Beachten Sie das Auftreten der vier obigen Terme im Theorem – Posterior-Wahrscheinlichkeit, Likelihood-Wahrscheinlichkeit, Prior-Wahrscheinlichkeit und Beweis.
Lesen Sie: Naive Bayes erklärt
Anwendung des Bayes-Theorems beim maschinellen Lernen
Der Naive-Bayes-Klassifikator, eine vereinfachte Version des Bayes-Theorems, wird als Klassifizierungsalgorithmus verwendet, um Daten genau und schnell in verschiedene Klassen zu klassifizieren.
Sehen wir uns an, wie der Naive-Bayes-Klassifikator als Klassifikationsalgorithmus angewendet werden kann.
- Betrachten Sie ein allgemeines Beispiel: X ist ein Vektor, der aus 'n' Attributen besteht, dh X = {x1, x2, x3, …, xn}.
- Angenommen, wir haben 'm' Klassen {C1, C2, …, Cm}. Unser Klassifikator muss vorhersagen, dass X zu einer bestimmten Klasse gehört. Die Klasse, die die höchste Posterior-Wahrscheinlichkeit liefert, wird als beste Klasse ausgewählt. Mathematisch gesehen wird der Klassifikator für die Klasse Ci genau dann vorhersagen, wenn P(Ci | X) > P(Cj | X). Anwendung des Satzes von Bayes:
P(Ci | X) = [P(X | Ci) * P(Ci)] / P(X)
- Da P(X) bedingungsunabhängig ist, ist es für jede Klasse konstant. Um also P(Ci | X) zu maximieren, müssen wir [P(X | Ci) * P(Ci)] maximieren. Da jede Klasse gleich wahrscheinlich ist, haben wir P(C1) = P(C2) = P(C3) … = P(Cn). Letztendlich müssen wir also nur P(X | Ci) maximieren.
- Da der typische große Datensatz wahrscheinlich mehrere Attribute hat, ist es rechenintensiv, die P(X | Ci)-Operation für jedes Attribut durchzuführen. Hier kommt die klassenbedingte Unabhängigkeit ins Spiel, um das Problem zu vereinfachen und die Rechenkosten zu reduzieren. Unter klassenbedingter Unabhängigkeit verstehen wir, dass wir die Werte des Attributs als bedingt voneinander unabhängig betrachten. Dies ist die Naive-Bayes-Klassifikation.
P(Xi | C) = P(x1 | C) * P(x2 | C) *… * P(xn | C)
Es ist jetzt einfach, die kleineren Wahrscheinlichkeiten zu berechnen. Eine wichtige Sache, die hier zu beachten ist: Da xk zu jedem Attribut gehört, müssen wir auch prüfen, ob das Attribut, mit dem wir es zu tun haben, kategorial oder stetig ist .
- Wenn wir ein kategoriales Attribut haben, sind die Dinge einfacher. Wir können einfach die Anzahl der Instanzen der Klasse Ci zählen, die aus dem Wert xk für das Attribut k bestehen, und diese dann durch die Anzahl der Instanzen der Klasse Ci dividieren.
- Wenn wir ein kontinuierliches Attribut haben und davon ausgehen, dass wir eine Normalverteilungsfunktion haben, wenden wir die folgende Formel an, wobei der Mittelwert ? und Standardabweichung ?:
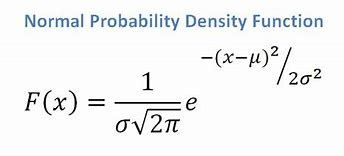

Quelle
Letztendlich haben wir P(x | Ci) = F(xk, ?k, ?k).
- Jetzt haben wir alle Werte, die wir brauchen, um das Bayes-Theorem für jede Klasse Ci zu verwenden. Unsere vorhergesagte Klasse wird die Klasse sein, die die höchste Wahrscheinlichkeit P(X | Ci) * P(Ci) erreicht.
Beispiel: Kunden einer Buchhandlung vorausschauend klassifizieren
Wir haben folgenden Datensatz aus einer Buchhandlung:
| Zeitalter | Einkommen | Student | Kreditbeurteilung | Kauft_Buch |
| Jugend | Hoch | Nein | Messe | Nein |
| Jugend | Hoch | Nein | Exzellent | Nein |
| Im mittleren Alter | Hoch | Nein | Messe | Jawohl |
| Senior | Mittel | Nein | Messe | Jawohl |
| Senior | Niedrig | Jawohl | Messe | Jawohl |
| Senior | Niedrig | Jawohl | Exzellent | Nein |
| Im mittleren Alter | Niedrig | Jawohl | Exzellent | Jawohl |
| Jugend | Mittel | Nein | Messe | Nein |
| Jugend | Niedrig | Jawohl | Messe | Jawohl |
| Senior | Mittel | Jawohl | Messe | Jawohl |
| Jugend | Mittel | Jawohl | Exzellent | Jawohl |
| Im mittleren Alter | Mittel | Nein | Exzellent | Jawohl |
| Im mittleren Alter | Hoch | Jawohl | Messe | Jawohl |
| Senior | Mittel | Nein | Exzellent | Nein |
Wir haben Attribute wie Alter, Einkommen, Student und Bonität. Unsere Klasse buys_book hat zwei Ergebnisse: Ja oder Nein.
Unser Ziel ist es, anhand der folgenden Attribute zu klassifizieren:
X = {Alter = Jugend, Student = ja, Einkommen = mittel, credit_rating = fair}.
Wie wir bereits gezeigt haben, müssen wir zur Maximierung von P(Ci | X) [ P(X | Ci) * P(Ci) ] für i = 1 und i = 2 maximieren.
Daher ist P(buys_book = yes) = 9/14 = 0,643
P(buys_book = nein) = 5/14 = 0,357
P(Alter = Jugend | kauft_Buch = ja) = 2/9 = 0,222
P(Alter = Jugend | kauft_Buch = nein) =3/5 = 0,600
P(Einkommen = mittel | Käufe_Buch = Ja) = 4/9 = 0,444
P(Einkommen = mittel | Käufe_Buch = nein) = 2/5 = 0,400
P(Schüler = ja | kauft_buch = ja) = 6/9 = 0,667
P(Schüler = ja | kauft_buch = nein) = 1/5 = 0,200
P(credit_rating = fair | buys_book = yes) = 6/9 = 0,667
P(credit_rating = fair | buys_book = nein) = 2/5 = 0,400
Unter Verwendung der oben berechneten Wahrscheinlichkeiten haben wir
P(X | buys_book = ja) = 0,222 x 0,444 x 0,667 x 0,667 = 0,044
Ähnlich,
P(X | buys_book = nein) = 0,600 x 0,400 x 0,200 x 0,400 = 0,019
Welche Klasse liefert Ci das Maximum P(X|Ci)*P(Ci)? Wir berechnen:
P(X | kauft_buch = ja)* P(kauft_buch = ja) = 0,044 x 0,643 = 0,028
P(X | kauft_buch = nein)* P(kauft_buch = nein) = 0,019 x 0,357 = 0,007

Vergleicht man die beiden oben genannten, da 0,028 > 0,007, sagt der Naive-Bayes-Klassifikator voraus, dass der Kunde mit den oben genannten Attributen ein Buch kaufen wird .
Kasse: Ideen und Themen für Machine Learning-Projekte
Ist der Bayes'sche Klassifikator eine gute Methode?
Algorithmen, die auf dem Bayes-Theorem im maschinellen Lernen basieren, liefern Ergebnisse, die mit anderen Algorithmen vergleichbar sind, und Bayessche Klassifikatoren gelten im Allgemeinen als einfache Methoden mit hoher Genauigkeit. Es sollte jedoch darauf geachtet werden, dass Bayes'sche Klassifikatoren besonders geeignet sind, wenn die Annahme der klassenbedingten Unabhängigkeit gültig ist, und nicht in allen Fällen. Ein weiteres praktisches Problem besteht darin, dass das Erfassen aller Wahrscheinlichkeitsdaten möglicherweise nicht immer durchführbar ist.
Fazit
Das Bayes-Theorem hat viele Anwendungen im maschinellen Lernen, insbesondere bei klassifikationsbasierten Problemen. Die Anwendung dieser Familie von Algorithmen beim maschinellen Lernen erfordert die Vertrautheit mit Begriffen wie Prior-Wahrscheinlichkeit und Posterior-Wahrscheinlichkeit. In diesem Artikel haben wir die Grundlagen des Bayes-Theorems und seine Verwendung bei maschinellen Lernproblemen besprochen und ein Klassifizierungsbeispiel durchgearbeitet.
Da das Bayes-Theorem einen wesentlichen Bestandteil klassifikationsbasierter Algorithmen im maschinellen Lernen darstellt, können Sie mehr über das Advanced Certificate Program in Machine Learning & NLP von upGrad erfahren . Dieser Kurs wurde unter Berücksichtigung verschiedener Arten von Studenten entwickelt, die sich für maschinelles Lernen interessieren, und bietet 1-1-Mentoring und vieles mehr.
Warum verwenden wir das Bayes-Theorem beim maschinellen Lernen?
Das Bayes-Theorem ist eine Methode zur Berechnung bedingter Wahrscheinlichkeiten oder der Wahrscheinlichkeit, dass ein Ereignis eintritt, wenn zuvor ein anderes aufgetreten ist. Eine bedingte Wahrscheinlichkeit kann zu genaueren Ergebnissen führen, indem zusätzliche Bedingungen einbezogen werden – mit anderen Worten, mehr Daten. Um beim maschinellen Lernen korrekte Schätzungen und Wahrscheinlichkeiten zu erhalten, werden bedingte Wahrscheinlichkeiten benötigt. Angesichts der zunehmenden Verbreitung dieses Bereichs in einer Vielzahl von Bereichen ist es wichtig, die Bedeutung von Algorithmen und Ansätzen wie dem Bayes-Theorem beim maschinellen Lernen zu verstehen.
Ist Bayes'scher Klassifikator eine gute Wahl?
Beim maschinellen Lernen liefern auf dem Bayes-Theorem basierende Algorithmen Ergebnisse, die mit denen anderer Methoden vergleichbar sind, und Bayessche Klassifikatoren gelten weithin als einfache hochgenaue Ansätze. Es ist jedoch wichtig zu bedenken, dass Bayes'sche Klassifikatoren am besten verwendet werden, wenn die Bedingung der klassenbedingten Unabhängigkeit korrekt ist, nicht unter allen Umständen. Eine weitere Überlegung ist, dass es nicht immer möglich ist, alle Wahrscheinlichkeitsdaten zu erhalten.
Wie lässt sich das Bayes Theorem praktisch anwenden?
Das Bayes-Theorem berechnet die Wahrscheinlichkeit des Auftretens auf der Grundlage neuer Beweise, die damit zusammenhängen oder zusammenhängen könnten. Die Methode kann auch verwendet werden, um zu sehen, wie sich hypothetische neue Informationen auf die Wahrscheinlichkeit eines Ereignisses auswirken, vorausgesetzt, die neuen Informationen sind wahr. Nehmen Sie zum Beispiel eine einzelne Karte, die aus einem Stapel von 52 Karten ausgewählt wird. Die Wahrscheinlichkeit, dass die Karte ein König wird, beträgt 4 geteilt durch 52 oder 1/13 oder ungefähr 7,69 Prozent. Denken Sie daran, dass das Deck vier Könige enthält. Nehmen wir an, es wird aufgedeckt, dass die gewählte Karte eine Bildkarte ist. Da es 12 Bildkarten in einem Deck gibt, beträgt die Wahrscheinlichkeit, dass die gezogene Karte ein König ist, 4 geteilt durch 12 oder ungefähr 33,3 Prozent.
