Bayes-Theorem mit Beispiel erklärt – Vollständiger Leitfaden

Einführung

Was ist der Satz von Bayes?

Der Satz von Bayes wird zur Berechnung einer bedingten Wahrscheinlichkeit verwendet, bei der die Intuition oft versagt. Obwohl das Theorem in der Wahrscheinlichkeit weit verbreitet ist, wird es auch im Bereich des maschinellen Lernens angewendet. Seine Verwendung beim maschinellen Lernen umfasst die Anpassung eines Modells an einen Trainingsdatensatz und die Entwicklung von Klassifizierungsmodellen.

Was ist bedingte Wahrscheinlichkeit?

Eine bedingte Wahrscheinlichkeit wird normalerweise als die Wahrscheinlichkeit eines Ereignisses beim Eintreten eines anderen Ereignisses definiert.

• Wenn A und B zwei Ereignisse sind, dann kann die bedingte Wahrscheinlichkeit als P(A gegeben B) oder P(A|B) bezeichnet werden.
• Die bedingte Wahrscheinlichkeit kann aus der gemeinsamen Wahrscheinlichkeit berechnet werden (A | B) = P(A, B) / P(B)

• Die bedingte Wahrscheinlichkeit ist nicht symmetrisch; Zum Beispiel P(A | B) != P(B | A)

Andere Möglichkeiten zum Berechnen der bedingten Wahrscheinlichkeit umfassen die Verwendung der anderen bedingten Wahrscheinlichkeit, d. h

P(A|B) = P(B|A) * P(A) / P(B)

Rückwärts wird auch verwendet

P(B|A) = P(A|B) * P(B) / P(A)

Diese Art der Berechnung ist nützlich, wenn es schwierig ist, die gemeinsame Wahrscheinlichkeit zu berechnen. Andernfalls, wenn die umgekehrte bedingte Wahrscheinlichkeit verfügbar ist, wird die Berechnung dadurch einfach.

Diese alternative Berechnung der bedingten Wahrscheinlichkeit wird als Bayes-Regel oder Bayes-Theorem bezeichnet. Es ist nach der Person benannt, die es zuerst beschrieben hat, „Reverend Thomas Bayes“.

Der Satz der Formel von Bayes

Das Bayes-Theorem ist eine Methode zur Berechnung der bedingten Wahrscheinlichkeit, wenn die gemeinsame Wahrscheinlichkeit nicht verfügbar ist. Manchmal kann nicht direkt auf den Nenner zugegriffen werden. In solchen Fällen ist die alternative Berechnungsmethode wie folgt:

P(B) = P(B|A) * P(A) + P(B|nicht A) * P(nicht A)

Dies ist die Formulierung des Satzes von Bayes, der eine alternative Berechnung von P(B) zeigt.

P(A|B) = P(B|A) * P(A) / P(B|A) * P(A) + P(B|nicht A) * P(nicht A)

Die obige Formel kann mit Klammern um den Nenner beschrieben werden

P(A|B) = P(B|A) * P(A) / (P(B|A) * P(A) + P(B|nicht A) * P(nicht A))

Auch wenn wir P(A) haben, dann kann P(nicht A) berechnet werden als

P(nicht A) = 1 – P(A)

Wenn wir P(nicht B|nicht A) haben, dann kann P(B|nicht A) in ähnlicher Weise berechnet werden als

P(B|nicht A) = 1 – P(nicht B|nicht A)

Satz von Bayes der bedingten Wahrscheinlichkeit

Das Bayes-Theorem besteht aus mehreren Begriffen, deren Namen basierend auf dem Kontext ihrer Anwendung in der Gleichung angegeben werden.

Die Posterior-Wahrscheinlichkeit bezieht sich auf das Ergebnis von P(A|B) und die Prior-Wahrscheinlichkeit bezieht sich auf P(A).

• P(A|B): Posterior-Wahrscheinlichkeit.
• P(A): Vorherige Wahrscheinlichkeit.

In ähnlicher Weise werden P(B|A) und P(B) als Wahrscheinlichkeit und Evidenz bezeichnet.

• P(B|A): Wahrscheinlichkeit.
• P(B): Beweis.

Daher kann das Bayes-Theorem der bedingten Wahrscheinlichkeit wie folgt umformuliert werden:

Posterior = Wahrscheinlichkeit * Prior / Beweis

Wenn wir die Wahrscheinlichkeit berechnen müssen, dass es Feuer gibt, wenn es Rauch gibt, dann wird die folgende Gleichung verwendet:

P(Feuer|Rauch) = P(Rauch|Feuer) * P(Feuer) / P(Rauch)

Wobei P(Feuer) der Prior ist, P(Rauch|Feuer) die Wahrscheinlichkeit ist und P(Rauch) der Beweis ist.

Eine Illustration des Satzes von Bayes

Ein Beispiel des Bayes -Theorems wird beschrieben, um die Verwendung des Bayes-Theorems in einem Problem zu veranschaulichen.

Problem

Es sind drei mit A, B und C bezeichnete Kästchen vorhanden. Details der Boxen sind:

• Schachtel A enthält 2 rote und 3 schwarze Kugeln
• Box B enthält 3 rote und 1 schwarze Kugel
• Und Box C enthält 1 rote Kugel und 4 schwarze Kugeln

Alle drei Kisten sind identisch und haben die gleiche Wahrscheinlichkeit, dass sie aufgehoben werden. Wie groß ist also die Wahrscheinlichkeit, dass der rote Ball aus Box A aufgenommen wurde?

Lösung

E bezeichne das Ereignis, dass ein roter Ball aufgenommen wird, und A, B und C bezeichnen, dass der Ball aus ihren jeweiligen Kästen aufgenommen wird. Daher wäre die bedingte Wahrscheinlichkeit P(A|E), die berechnet werden muss.

Die vorhandenen Wahrscheinlichkeiten P(A) = P(B) = P(C) = 1 / 3, da alle Kisten die gleiche Wahrscheinlichkeit haben, ausgewählt zu werden.

P(E|A) = Anzahl der roten Bälle in Box A / Gesamtzahl der Bälle in Box A = 2 / 5

Ebenso ist P(E|B) = 3 / 4 und P(E|C) = 1 / 5

Dann Beweis P(E) = P(E|A)*P(A) + P(E|B)*P(B) + P(E|C)*P(C)

= (2/5) * (1/3) + (3/4) * (1/3) + (1/5) * (1/3) = 0,45

Daher ist P(A|E) = P(E|A) * P(A) / P(E) = (2/5) * (1/3) / 0,45 = 0,296

Beispiel für den Satz von Bayes

Das Bayes-Theorem gibt die Wahrscheinlichkeit eines „Ereignisses“ mit den gegebenen Informationen zu „Tests“ an.

• Es gibt einen Unterschied zwischen „Events“ und „Tests“. Zum Beispiel gibt es einen Test für eine Lebererkrankung, was etwas anderes ist, als tatsächlich eine Lebererkrankung zu haben, dh ein Ereignis.
• Seltene Ereignisse können eine höhere Falsch-Positiv-Rate aufweisen.

Beispiel 1

Wie hoch ist die Wahrscheinlichkeit, dass ein Patient eine Lebererkrankung hat, wenn er Alkoholiker ist?

„Alkoholiker sein“ ist hier der „Test“ (eine Art Lackmustest) für Lebererkrankungen.

• A ist das Ereignis, dh „Patient hat eine Lebererkrankung“.

Aus früheren Aufzeichnungen der Klinik geht hervor, dass 10 % der Patienten, die die Klinik betreten, an einer Lebererkrankung leiden.

Daher ist P(A)=0,10

• B ist der Lackmustest, dass „der Patient ein Alkoholiker ist“.

Frühere Aufzeichnungen der Klinik zeigten, dass 5 % der Patienten, die die Klinik betreten, Alkoholiker sind.

Daher ist P(B)=0,05

• Außerdem sind 7 % der Patienten, bei denen eine Lebererkrankung diagnostiziert wird, Alkoholiker. Dies definiert die B|A: Die Wahrscheinlichkeit, dass ein Patient alkoholkrank ist, liegt bei einer Lebererkrankung bei 7 %.

Gemäß der Bayes-Theorem - Formel

P(A|B) = (0,07 * 0,1)/0,05 = 0,14

Daher beträgt die Wahrscheinlichkeit einer Lebererkrankung bei einem alkoholkranken Patienten 0,14 (14 %).

Beispiel2

• Gefährliche Brände sind selten (1%)
• Aber Rauch ist ziemlich häufig (10%) aufgrund von Grillabenden,
• Und 90 % der gefährlichen Brände erzeugen Rauch

Wie hoch ist die Wahrscheinlichkeit eines gefährlichen Feuers bei Rauch?

Berechnung

P(Feuer|Rauch) =P(Feuer) P(Rauch|Feuer)/P(Rauch)

= 1 % x 90 %/10 %

= 9%

Beispiel 3

Wie hoch ist die Regenwahrscheinlichkeit tagsüber? Dabei bedeutet Regen Regen während des Tages und Wolke bedeutet bewölkter Morgen.

Die Wahrscheinlichkeit von Regen bei Cloud ist geschrieben P(Rain|Cloud)

P(Regen|Wolke) = P(Regen) P(Wolke|Regen)/P(Wolke)

P(Regen) ist die Regenwahrscheinlichkeit = 10 %

P(Wolke|Regen) ist die Wahrscheinlichkeit einer Wolke, vorausgesetzt, es regnet = 50 %

P(Wolke) ist die Wahrscheinlichkeit einer Wolke = 40 %

P(Regen|Wolken) = 0,1 x 0,5/0,4 = 0,125

Daher eine Regenwahrscheinlichkeit von 12,5 %.

Anwendungen

In der realen Welt gibt es mehrere Anwendungen des Bayes-Theorems. Die wenigen Hauptanwendungen des Theorems sind:

1. Modellierungshypothesen

Das Bayes-Theorem findet breite Anwendung im angewandten maschinellen Lernen und stellt eine Beziehung zwischen den Daten und einem Modell her. Angewandtes maschinelles Lernen verwendet den Prozess des Testens und Analysierens verschiedener Hypothesen zu einem bestimmten Datensatz.

Um die Beziehung zwischen den Daten und dem Modell zu beschreiben, liefert das Bayes-Theorem ein probabilistisches Modell.

P(h|D) = P(D|h) * P(h) / P(D)

Woher,

P(h|D): Posterior-Wahrscheinlichkeit der Hypothese

P(h): A-priori-Wahrscheinlichkeit der Hypothese.

Eine Erhöhung von P(D) verringert P(h|D). Umgekehrt, wenn P(h) und die Wahrscheinlichkeit zum Beobachten der gegebenen Hypothese der Daten zunehmen, dann steigt die Wahrscheinlichkeit von P(h|D).

2. Satz von Bayes zur Klassifikation

Die Klassifizierungsmethode beinhaltet die Kennzeichnung bestimmter Daten. Sie kann als Berechnung der bedingten Wahrscheinlichkeit einer Klassenbezeichnung bei gegebener Datenstichprobe definiert werden.

P(Klasse|Daten) = (P(Daten|Klasse) * P(Klasse)) / P(Daten)

Wobei P(Klasse|Daten) die Wahrscheinlichkeit der Klasse angesichts der bereitgestellten Daten ist.

Die Berechnung kann für jede Klasse durchgeführt werden. Den Eingangsdaten kann die Klasse mit der größten Wahrscheinlichkeit zugeordnet werden.

Die Berechnung der bedingten Wahrscheinlichkeit ist unter Bedingungen einer kleinen Anzahl von Beispielen nicht durchführbar. Daher ist die direkte Anwendung des Satzes von Bayes nicht durchführbar. Eine Lösung des Klassifizierungsmodells liegt in der vereinfachten Berechnung.

• Naive Bayes-Klassifikator

Das Bayes-Theorem berücksichtigt, dass Eingabevariablen von anderen Variablen abhängig sind, die die Komplexität der Berechnung verursachen. Daher wird die Annahme entfernt und jede Eingangsvariable als unabhängige Variable betrachtet. Als Ergebnis ändert sich das Modell von einem abhängigen zu einem unabhängigen bedingten Wahrscheinlichkeitsmodell. Es reduziert letztendlich die Komplexität.

Diese Vereinfachung des Satzes von Bayes wird als Naive Bayes bezeichnet. Es wird häufig für Klassifizierungs- und Vorhersagemodelle verwendet.

• Optimaler Bayes-Klassifikator

Dies ist eine Art Wahrscheinlichkeitsmodell, das die Vorhersage eines neuen Beispiels im gegebenen Trainingsdatensatz beinhaltet. Ein Beispiel für den Bayes Optimal Classifier ist „Was ist die wahrscheinlichste Klassifizierung der neuen Instanz angesichts der Trainingsdaten?“

Die Berechnung der bedingten Wahrscheinlichkeit einer neuen Instanz bei gegebenen Trainingsdaten kann durch die folgende Gleichung erfolgen

P(vj | D) = Summe {h in H} P(vj | hi) * P(hi | D)

Wobei vj eine neue zu klassifizierende Instanz ist,

H ist die Hypothesenmenge zur Klassifizierung der Instanz,

Hallo ist eine gegebene Hypothese,

P(vj | hi) ist die A-posteriori-Wahrscheinlichkeit für vi bei gegebener Hypothese hi, und

P(hi | D) ist die spätere Wahrscheinlichkeit der Hypothese hi bei gegebenen Daten D.

3. Verwendung des Bayes-Theorems beim maschinellen Lernen

Die häufigste Anwendung des Bayes-Theorems beim maschinellen Lernen ist die Entwicklung von Klassifizierungsproblemen. Andere Anwendungen als die Klassifizierung umfassen Optimierungs- und Gelegenheitsmodelle.

• Bayessche Optimierung

Es ist immer eine herausfordernde Aufgabe, eine Eingabe zu finden, die zu den minimalen oder maximalen Kosten einer gegebenen Zielfunktion führt. Bayes'sche Optimierung basiert auf dem Satz von Bayes und stellt einen Aspekt für die Suche nach einem globalen Optimierungsproblem bereit. Das Verfahren umfasst den Aufbau eines probabilistischen Modells (Ersatzfunktion), das Durchsuchen einer Erfassungsfunktion und die Auswahl von Kandidatenproben zum Bewerten der realen Zielfunktion.

Beim angewandten maschinellen Lernen wird die Bayes'sche Optimierung verwendet, um die Hyperparameter eines gut funktionierenden Modells abzustimmen.

• Bayesianische Glaubensnetzwerke

Beziehungen zwischen den Variablen können durch die Verwendung von Wahrscheinlichkeitsmodellen definiert werden. Sie werden auch zur Berechnung von Wahrscheinlichkeiten verwendet. Ein vollständig bedingtes Wahrscheinlichkeitsmodell kann die Wahrscheinlichkeiten aufgrund der großen Datenmenge möglicherweise nicht berechnen. Naive Bayes hat den Ansatz für die Berechnung vereinfacht. Es gibt noch ein weiteres Verfahren, bei dem ein Modell entwickelt wird, das auf der bekannten bedingten Abhängigkeit zwischen Zufallsvariablen und der bedingten Unabhängigkeit in anderen Fällen basiert. Das Bayes'sche Netz zeigt diese Abhängigkeit und Unabhängigkeit durch das probabilistische Graphenmodell mit gerichteten Kanten. Die bekannte bedingte Abhängigkeit wird als gerichtete Kanten dargestellt und die fehlenden Verbindungen stellen die bedingten Abhängigkeiten im Modell dar.

4. Bayessche Spam-Filterung

Spam-Filterung ist eine weitere Anwendung des Bayes-Theorems. Zwei Ereignisse sind vorhanden:

• Ereignis A: Die Nachricht ist Spam.
• Test X: Die Nachricht enthält bestimmte Wörter (X)

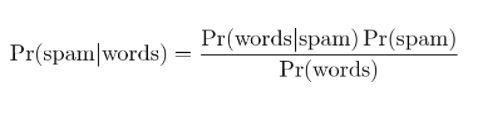
Mit der Anwendung des Bayes-Theorems kann anhand der „Testergebnisse“ vorhergesagt werden, ob es sich bei der Nachricht um Spam handelt. Die Analyse der Wörter in einer Nachricht kann die Wahrscheinlichkeit berechnen, dass es sich um eine Spam-Nachricht handelt. Durch das Training von Filtern mit wiederholten Nachrichten wird die Tatsache aktualisiert, dass die Wahrscheinlichkeit, dass bestimmte Wörter in der Nachricht enthalten sind, Spam wäre.

Eine Anwendung des Satzes von Bayes mit einem Beispiel

Ein Katalysatorhersteller stellt ein Gerät zum Testen von Fehlern in einem bestimmten Elektrokatalysator (EC) her. Der Katalysatorhersteller behauptet, dass der Test zu 97 % zuverlässig ist, wenn der EC defekt ist, und zu 99 % zuverlässig, wenn er fehlerfrei ist. Es kann jedoch erwartet werden, dass 4 % des EC bei Lieferung defekt sind. Die Bayes-Regel wird angewendet, um die wahre Zuverlässigkeit des Geräts festzustellen. Die grundlegenden Ereignissätze sind

A: EC ist defekt; A': EC ist fehlerfrei; B: EC wird als defekt getestet; B': Das EC wird auf Fehlerfreiheit getestet.

Die Wahrscheinlichkeiten wären

B/A: EC ist (bekanntermaßen) defekt und defekt getestet, P(B/A) = 0,97,

B'/A: EC ist (bekanntermaßen) defekt, aber fehlerfrei getestet, P(B'/A)=1-P(B/A)=0.03,

B/A': EC ist (bekanntermaßen) defekt, aber getestet defekt, P(B/A') = 1 - P(B'/A') = 0,01

B'/A: = EC ist (bekanntermaßen) fehlerfrei, und getestet fehlerfrei P(B'/A') = 0,99

Die nach dem Satz von Bayes berechneten Wahrscheinlichkeiten sind:

Die Berechnungswahrscheinlichkeit zeigt, dass eine hohe Wahrscheinlichkeit besteht, einwandfreie ECs zu verwerfen (etwa 20 %) und eine geringe Wahrscheinlichkeit, fehlerhafte ECs zu identifizieren (etwa 80 %).

Fazit

Eines der auffälligsten Merkmale eines Bayes-Theorems ist, dass aus wenigen Wahrscheinlichkeitsverhältnissen eine riesige Menge an Informationen gewonnen werden kann. Mit dem Mittel der Wahrscheinlichkeit kann die Wahrscheinlichkeit eines vorherigen Ereignisses in die spätere Wahrscheinlichkeit transformiert werden. Die Ansätze des Bayes-Theorems können in Bereichen der Statistik, Erkenntnistheorie und induktiven Logik angewendet werden.

Wenn Sie mehr über das Bayes-Theorem, KI und maschinelles Lernen erfahren möchten, sehen Sie sich das Executive PG-Programm von IIIT-B & upGrad in maschinellem Lernen und KI an, das für Berufstätige konzipiert ist und mehr als 450 Stunden strenges Training, 30+ Fälle bietet Studien und Aufgaben, IIIT-B-Alumni-Status, mehr als 5 praktische praktische Abschlussprojekte und Arbeitsunterstützung bei Top-Unternehmen.