ما هو التفكير بايزي؟ مقدمة ونظرية

لا تزال النظرية الإحصائية التي قدمها الإحصائي والفيلسوف الإنجليزي توماس بايز في القرن الثامن عشر الميلادي بمثابة ضوء إرشادي للعلماء والمحللين في جميع أنحاء العالم. اليوم ، يجد التفكير البايزي تطبيقًا في الطب والعلوم والتكنولوجيا والعديد من التخصصات الأخرى ويستمر في التأثير بقوة على نظرتنا للعالم والأفعال الناتجة.

كانت فكرة توماس بايز بسيطة للغاية. وفقًا لبايز ، يعتمد احتمال أن تكون الفرضية صحيحة على شرطين: مدى معقولية أنها تستند إلى ما نعرفه بالفعل (المعرفة السابقة) ومدى ملاءمتها للأدلة الجديدة. وبالتالي ، يختلف التفكير البايزي عن اختبار الفرضيات التقليدية في أن الأول يتضمن المعرفة السابقة قبل القفز إلى الاستنتاجات.

مع وضع المقدمة الأولية في الاعتبار ، دعونا نتعمق في مزيد من التفاصيل حول إحصائيات بايز.

إحصائيات بايزي

بعبارات بسيطة ، تطبق إحصائيات بايز الاحتمالات على المشكلات الإحصائية لتحديث المعتقدات السابقة في ضوء أدلة البيانات الجديدة. يعبر الاحتمال عن درجة من الاعتقاد في حدث معين.

قد تعتمد درجة الاعتقاد على المعرفة السابقة بالحدث بناءً على الافتراضات الشخصية أو نتائج التجارب السابقة. تستخدم إحصائيات بايز نظرية بايز لحساب الاحتمالات. تصف نظرية بايز بدورها الاحتمال الشرطي لحدث ما بناءً على أدلة جديدة ومعلومات سابقة متعلقة بالحدث.

مع أخذ ذلك في الاعتبار ، دعونا نركز على المفهوم الأساسي للاحتمال الشرطي قبل أن نفهم نظرية بايز في العمق.

احتمال مشروط

يمكن تعريف الاحتمال الشرطي على أنه احتمال وقوع حدث أو نتيجة بناءً على حدوث حدث أو نتيجة سابقة. يتم حسابه بضرب احتمالية الحدث السابق باحتمالية الحدث اللاحق أو الشرطي.

دعنا نلقي نظرة على مثال لفهم المفهوم بشكل أفضل .

• الحدث (أ) هو تنظيم الأسرة والنزهة في نزهة. هناك احتمال بنسبة 80٪ أن الأسرة ستذهب في نزهة.
• الحدث ب هو أنها ستمطر في اليوم الذي تخرج فيه الأسرة في نزهة. تشير توقعات الطقس إلى أن هناك فرصة 60٪ لهطول الأمطار في يوم النزهة.
• ومن هنا فإن احتمال ذهاب الأسرة للنزهة وهطول الأمطار يُحسب على النحو التالي:

P (النزهة والمطر) = P (المطر | النزهة) P (النزهة) = (0.60) * (0.80) = 0.48

في المثال أعلاه ، ينظر الاحتمال الشرطي إلى الحدثين A و B في علاقة مع بعضهما البعض ، أي احتمال أن تذهب العائلة إلى النزهة وتمطر أيضًا في نفس اليوم.

ومن ثم ، يختلف الاحتمال الشرطي عن الاحتمال غير المشروط لأن الأخير يشير إلى احتمال حدوث حدث بغض النظر عما إذا كان قد حدث أي حدث أو أحداث أخرى أو وجود أي شروط أخرى.

صيغة الاحتمال الشرطي

تأتي معادلة الاحتمال الشرطي من قاعدة الضرب الاحتمالية:

P (A و B) أو P (AUB) = P (B معطى A) أو P (B | A) * P (A)

في المعادلة أعلاه ، P (A و B) هو الاحتمال المشترك ، في إشارة إلى احتمال وقوع حدثين أو أكثر في وقت واحد. وهي مكتوبة أيضًا كـ P (A ، B).

إليك كيفية استنتاج معادلة الاحتمال الشرطي من قاعدة الضرب:

الخطوة 1: اكتب قاعدة الضرب.

الفوسفور (أ و ب) = ف (ب | أ) * ف (أ)

الخطوة 2: قسّم طرفي المعادلة على P (A).

الفوسفور (A و B) / P (A) = P (B | A) * P (A) / P (A)

الخطوة 3: قم بإلغاء P (A) على الجانب الأيمن من المعادلة.

الفوسفور (أ و ب) / ف (أ) = ف (ب | أ)

الخطوة 4: أعد كتابة المعادلة.

الفوسفور (أ و ب) = الفوسفور (ب | أ) / ف (أ)

وبالتالي ، فإن صيغة الاحتمال الشرطي تُعطى على النحو التالي:

الفوسفور (أ و ب) = الفوسفور (ب | أ) / ف (أ)

مبرهنة بايز

باستخدام نظرية بايز ، يمكننا تحديث معتقداتنا وقناعاتنا بناءً على أدلة جديدة وذات صلة. على سبيل المثال ، إذا كنا نحاول معرفة احتمالية إصابة شخص معين بالسرطان ، فسنفترض عمومًا أنها النسبة المئوية للسكان المصابين بالسرطان. ومع ذلك ، إذا قدمنا ​​أدلة إضافية ، مثل أن الشخص المعني هو مدخن منتظم ، فيمكننا تحديث تصورنا (وبالتالي الاحتمال) لأن احتمال الإصابة بالسرطان يكون أعلى إذا كان الفرد مدخنًا. ومن ثم ، فإننا نستخدم كل من معرفتنا السابقة والأدلة الإضافية لتحسين تقديراتنا.

صيغة نظرية بايز

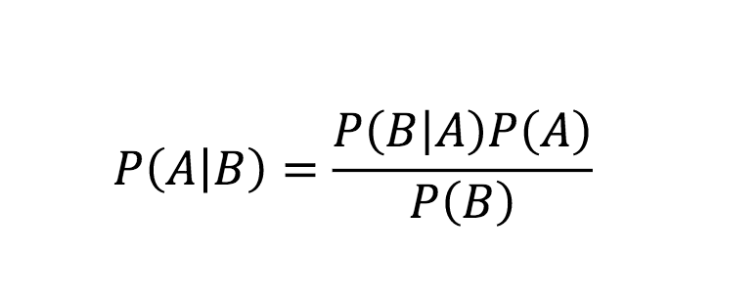
مصدر

المعادلة أعلاه هي قاعدة بايز. الآن ، دعونا ننظر في الاشتقاق التدريجي لمعادلة نظرية بايز.

الخطوة 1: ضع في اعتبارك حدثين ، A و B. A هو الحدث الذي نريد حساب احتماله و B هو الدليل الإضافي المرتبط بـ A.

الخطوة 2: اكتب العلاقة بين الاحتمال المشترك والاحتمال الشرطي للأحداث A و B.

الفوسفور (أ ، ب) = ف (أ | ب) * ف (ب) = ف (ب ، أ) = ف (ب | أ) * ف (أ)

الخطوة 3: قم بتعيين شرطي الاحتمال الشرطي على قدم المساواة مع بعضهما البعض.

الفوسفور (أ | ب) * ف (ب) = ف (ب | أ) * ف (أ)

الخطوة 4: قسّم طرفي المعادلة على P (B).

ف (أ | ب) * ف (ب) / ف (ب) = ف (ب | أ) * ف (أ) / ف (ب)

الخطوة 5: قم بإلغاء P (B) على الجانب الأيسر من المعادلة.

الفوسفور (A | B) = P (B | A) * P (A) / P (B)

وهكذا نحصل على صيغة نظرية بايز على النحو التالي:

الفوسفور (A | B) = P (B | A) * P (A) / P (B)

فهم المصطلحات في معادلة نظرية بايز

الفوسفور (A | B) = P (B | A) * P (A) / P (B)

• يُطلق على P (A | B) الاحتمال اللاحق أو الاحتمال الذي نحاول تقديره. بناءً على المثال السابق ، سيكون الاحتمال اللاحق هو احتمال إصابة الشخص بالسرطان ، بالنظر إلى أن الشخص مدخن منتظم.
• يُطلق على P (B | A) اسم الاحتمال ، في إشارة إلى احتمال اكتشاف الدليل الإضافي ، بالنظر إلى فرضيتنا الأولية. في المثال أعلاه ، الاحتمال هو احتمال أن يكون الشخص مدخنًا ، نظرًا لإصابته بالسرطان.
• P (A) هو الاحتمال المسبق أو احتمال فرضيتنا دون أي دليل أو معلومات إضافية. في المثال أعلاه ، الاحتمال السابق هو احتمال الإصابة بالسرطان.
• P (B) هو الاحتمال الهامشي أو الاحتمال الكلي لملاحظة الدليل. في سياق المثال أعلاه ، فإن الاحتمال الهامشي هو احتمال أن تكون مدخنًا.

مثال بسيط لفهم نظرية بايز

باستخدام بعض الأرقام الافتراضية في المثال السابق ، سنرى تأثير تطبيق نظرية بايز.

لنفترض أن احتمال الإصابة بالسرطان هو 0.06 ، أي أن 6٪ من الناس مصابون بالسرطان. الآن ، لنفترض أن احتمال أن تكون مدخنًا هو 0.20 أو 20٪ من الأشخاص مدخنون ، وأن 30٪ من المصابين بالسرطان مدخنون. إذن ، P (مدخن | السرطان) = 0.30.

في البداية ، يكون احتمال الإصابة بالسرطان مجرد 0.06 (سابقًا). لكن باستخدام الدليل الجديد ، يمكننا حساب P (السرطان | المدخن) = P ((المدخن | السرطان) * P (السرطان)) / P (المدخن) = (0.30 * 0.06) / (0.20) = 0.09.

تعلم دورات علوم البيانات عبر الإنترنت من أفضل الجامعات في العالم. اربح برامج PG التنفيذية أو برامج الشهادات المتقدمة أو برامج الماجستير لتتبع حياتك المهنية بشكل سريع.

المضي قدمًا: إتقان مفاهيم الإحصاء لمهنة في علوم البيانات أو التعلم الآلي

أثرت منصة التعلم للتعليم العالي التابعة لشركة upGrad على أكثر من 500000 من المهنيين العاملين في جميع أنحاء العالم من خلال عدد كبير من الدورات وخبرات التعلم الغامرة. مع وجود 40.000+ قاعدة متعلم منتشرة في أكثر من 85 دولة ، تضمن دورات upGrad ذات الصلة بالصناعة تعزيز حياتك المهنية في المجال الذي تختاره.

ماجستير العلوم في علوم البيانات عبارة عن دورة مدتها 18 شهرًا تنقل المهارات الأساسية في الإحصاء والتحليل التنبئي والتعلم الآلي وتحليلات البيانات الضخمة وتصور البيانات وما إلى ذلك.

يسلط الضوء على البرنامج:

• درجة الماجستير من جامعة ليفربول جون مورس والمدير التنفيذي PGP من IIIT بنغالور
• أكثر من 500 ساعة من المحتوى ، وأكثر من 60 دراسة حالة ومشروعًا ، وأكثر من 20 جلسة مباشرة ، وأكثر من 14 لغة وأدوات برمجة
• شبكات الصناعة ، وجلسات حل الشك ، ودعم التعلم

برنامج الشهادة المتقدم في التعلم الآلي والتعلم العميق عبارة عن دورة تدريبية صارمة مدتها 6 أشهر مع فرص للتواصل مع الأقران ، ومشاريع عملية ، وإرشاد صناعي ، ومساعدة مهنية بزاوية 360 درجة.

يسلط الضوء على البرنامج:

• تقدير مرموق من IIIT بنغالور
• 240+ ساعة من المحتوى ، وأكثر من 5 دراسات حالة ، ومشاريع ، و 24+ جلسة مباشرة ، وتغطية 12 لغة برمجة وأدوات ومكتبات
• 1: 8 جلسات تدريب جماعية وجلسات إرشادية 1: 1 مع خبراء الصناعة

خاتمة

يدعم التفكير البايزي العديد من مجالات التفكير والاستعلام والمعتقدات البشرية ، على الرغم من أن معظمنا لا يدرك ذلك. من فحص السرطان والاحتباس الحراري إلى السياسة النقدية وتقييم المخاطر والتأمين ، يعتبر التفكير البايزي أمرًا أساسيًا. يُعتقد أن عالم الرياضيات البريطاني الشهير آلان تورينج قد استخدم النهج البايزي لكسر كود الألغاز الألماني خلال الحرب العالمية الثانية.

قم بالتسجيل في upGrad وعزز معرفتك بالمفاهيم الإحصائية الأساسية والمزيد!