تعلم خوارزمية Naive Bayes للتعلم الآلي [مع أمثلة]
نشرت: 2021-02-25جدول المحتويات
مقدمة
في الرياضيات والبرمجة ، عادةً ما تكون بعض أبسط الحلول هي الأقوى. تأتي خوارزمية Bayes الساذجة كمثال كلاسيكي لهذا البيان. حتى مع التقدم والتطور القوي والسريع في مجال التعلم الآلي ، لا تزال خوارزمية Naive Bayes قوية كواحدة من أكثر الخوارزميات استخدامًا وكفاءة. تجد خوارزمية Bayes الساذجة تطبيقاتها في مجموعة متنوعة من المشكلات بما في ذلك مهام التصنيف ومشكلات معالجة اللغة الطبيعية (NLP).
تعمل الفرضية الرياضية لنظرية بايز كمفهوم أساسي وراء خوارزمية بايز السذاجة. في هذه المقالة ، سنستعرض أساسيات نظرية بايز ، خوارزمية Naive Bayes جنبًا إلى جنب مع تنفيذها في Python مع مثال مشكلة في الوقت الفعلي. إلى جانب ذلك ، سننظر أيضًا في بعض مزايا وعيوب خوارزمية Naive Bayes مقارنةً بمنافسيها.
أساسيات الاحتمالية
قبل أن نبدأ في فهم نظرية Bayes وخوارزمية Naive Bayes ، دعونا نزيد من معرفتنا الحالية بأساسيات الاحتمالية.
كما نعلم جميعًا بالتعريف ، بالنظر إلى الحدث A ، يتم إعطاء احتمال حدوث ذلك الحدث بواسطة P (A). في الاحتمال ، يُطلق على الحدثين A و B على أنهما حدثان مستقلان إذا كان وقوع الحدث A لا يغير احتمال حدوث الحدث B والعكس صحيح. من ناحية أخرى ، إذا غيّر حدث واحد احتمالية الآخر ، فسيتم تسميتها كأحداث تابعة.
دعونا نتعرف على مصطلح جديد يسمى الاحتمال الشرطي . في الرياضيات ، يُعرَّف الاحتمال الشرطي لحدثين A و B المقدمين من P (A | B) على أنه احتمال حدوث الحدث A نظرًا لأن الحدث B قد حدث بالفعل. اعتمادًا على العلاقة بين الحدثين أ و ب فيما يتعلق بما إذا كانا تابعين أو مستقلين ، يتم حساب الاحتمال الشرطي بطريقتين.
- يتم إعطاء الاحتمال الشرطي لحدثين تابعين A و B بواسطة P (A | B) = P (A و B) / P (B)
- يتم إعطاء التعبير عن الاحتمال الشرطي لحدثين مستقلين A و B بواسطة P (A | B) = P (A)
بمعرفة الرياضيات الكامنة وراء الاحتمالات والاحتمالات الشرطية ، دعنا ننتقل الآن نحو نظرية بايز.

مبرهنة بايز
في نظرية الإحصاء والاحتمالات ، تُستخدم نظرية بايز المعروفة أيضًا باسم قاعدة بايز لتحديد الاحتمال الشرطي للأحداث. بعبارة أخرى ، تصف نظرية بايز احتمالية وقوع حدث بناءً على معرفة مسبقة بالظروف التي قد تكون ذات صلة بالحدث.
لفهمها بطريقة أبسط ، ضع في اعتبارك أننا بحاجة إلى معرفة احتمال ارتفاع سعر المنزل للغاية. إذا علمنا بالمعايير الأخرى مثل وجود المدارس والمتاجر الطبية والمستشفيات القريبة ، فيمكننا إجراء تقييم أكثر دقة لها. هذا هو بالضبط ما تؤديه نظرية بايز.
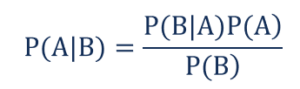
مثل ذلك،
- P (A | B) - الاحتمال الشرطي لحدوث الحدث A ، نظرًا لحدوث الحدث B المعروف أيضًا باسم الاحتمال الخلفي .
- P (B | A) - الاحتمال الشرطي لحدوث الحدث B ، نظرًا لحدوث الحدث A المعروف أيضًا باسم احتمالية الاحتمال .
- P (A) - احتمال وقوع الحدث A المعروف أيضًا باسم الاحتمال المسبق.
- P (B) - احتمال وقوع الحدث B المعروف أيضًا باسم الاحتمال الهامشي.
لنفترض أن لدينا مشكلة بسيطة في التعلم الآلي مع المتغيرات المستقلة 'n' والمتغير التابع وهو الناتج عبارة عن قيمة منطقية (صواب أو خطأ). لنفترض أن السمات المستقلة ذات طبيعة قاطعة ، فلنأخذ في الاعتبار فئتين لهذا المثال. ومن ثم ، باستخدام هذه البيانات ، نحتاج إلى حساب قيمة احتمال الاحتمال ، P (B | A).
ومن ثم ، عند ملاحظة ما سبق ، وجدنا أننا بحاجة إلى حساب معلمات 2 * (2 ^ n -1 ) من أجل تعلم نموذج التعلم الآلي هذا. وبالمثل ، إذا كان لدينا 30 سمة مستقلة منطقية ، فسيكون العدد الإجمالي للمعلمات التي سيتم حسابها قريبًا من 3 مليارات وهي تكلفة حسابية عالية للغاية.
أدت هذه الصعوبة في بناء نموذج التعلم الآلي باستخدام نظرية بايز إلى ولادة وتطوير خوارزمية بايز السذاجة.
خوارزمية بايز ساذجة
لكي تكون عملية ، يجب تقليل التعقيد المذكور أعلاه لنظرية بايز. يتم تحقيق ذلك بالضبط في خوارزمية Naive Bayes من خلال وضع افتراضات قليلة. الافتراضات الموضوعة هي أن كل ميزة تقدم مساهمة مستقلة ومتساوية في النتيجة.
خوارزمية بايز الساذجة هي خوارزمية تعلم خاضعة للإشراف وتستند إلى نظرية بايز التي تستخدم بشكل أساسي في حل مشاكل التصنيف. إنها واحدة من أبسط وأدق المصنفات التي تبني نماذج التعلم الآلي لعمل تنبؤات سريعة. رياضيا ، هو مصنف احتمالي لأنه يقوم بالتنبؤات باستخدام دالة الاحتمال للأحداث.
مثال مشكلة
من أجل فهم المنطق الكامن وراء الافتراضات ، دعنا ننتقل إلى مجموعة بيانات بسيطة للحصول على حدس أفضل.
| لون | اكتب | أصل | سرقة؟ |
| أسود | سيدان | مستورد | نعم |
| أسود | سيارات الدفع الرباعي | مستورد | رقم |
| أسود | سيدان | محلي | نعم |
| أسود | سيدان | مستورد | رقم |
| بني | سيارات الدفع الرباعي | محلي | نعم |
| بني | سيارات الدفع الرباعي | محلي | رقم |
| بني | سيدان | مستورد | رقم |
| بني | سيارات الدفع الرباعي | مستورد | نعم |
| بني | سيدان | محلي | رقم |
من مجموعة البيانات المذكورة أعلاه ، يمكننا اشتقاق مفاهيم الافتراضين اللذين حددناهما لخوارزمية Naive Bayes أعلاه.
- الافتراض الأول هو أن جميع الميزات مستقلة عن بعضها البعض. وهنا نرى أن كل سمة مستقلة مثل اللون "الأحمر" مستقل عن نوع وأصل السيارة.
- بعد ذلك ، يجب إعطاء كل ميزة أهمية متساوية. وبالمثل ، فإن معرفة نوع السيارة وأصلها فقط لا يكفي للتنبؤ بمخرجات المشكلة. ومن ثم ، لا يعد أي من المتغيرات غير ذي صلة ، وبالتالي فإنها تقدم جميعها مساهمة متساوية في النتيجة.
لتلخيص ذلك ، يكون A و B مستقلين بشكل مشروط بالنظر إلى C إذا وفقط إذا ، بالنظر إلى معرفة حدوث C ، فإن معرفة ما إذا كان A يحدث لا يوفر معلومات عن احتمال حدوث B ، ومعرفة ما إذا كان B يحدث لا يوفر معلومات عن احتمالية حدوث "أ". هذه الافتراضات تجعل خوارزمية بايز ساذجة . ومن هنا الاسم ، خوارزمية بايز السذاجة.
ومن ثم بالنسبة للمشكلة المذكورة أعلاه ، يمكن إعادة كتابة نظرية بايز على النحو التالي -
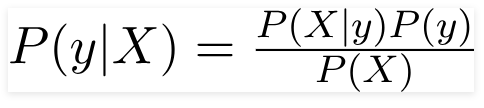
مثل ذلك،
- المتجه المستقل ، X = (x 1 ، x 2 ، x 3 …… x n ) يمثل ميزات مثل اللون والنوع وأصل السيارة.
- متغير الإخراج ، y له نتيجتان فقط نعم أو لا.
ومن ثم ، من خلال استبدال القيم المذكورة أعلاه ، نحصل على صيغة Naive Bayes كـ ،
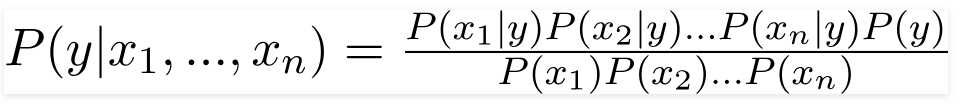
من أجل حساب الاحتمال اللاحق P (y | X) ، يتعين علينا إنشاء جدول تردد لكل سمة مقابل المخرجات. ثم نقوم بتحويل جداول التردد إلى جداول الاحتمالات وبعد ذلك نستخدم أخيرًا معادلة Naive Bayesian لحساب الاحتمال اللاحق لكل فئة. يتم اختيار الفئة ذات الاحتمالية اللاحقة الأعلى كنتيجة للتنبؤ. فيما يلي جداول التكرار والاحتمالية لجميع المتنبئين الثلاثة.
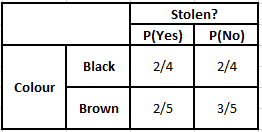
جدول التردد لجدول احتمالية اللون للون
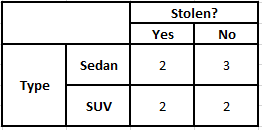
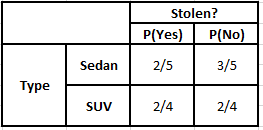
جدول التردد للنوع جدول احتمالية النوع
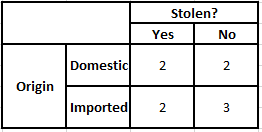
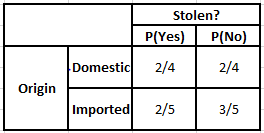
الجدول التكراري للمنشأ جدول احتمالية المنشأ

ضع في اعتبارك الحالة التي نحتاج فيها إلى حساب الاحتمالات اللاحقة للشروط الموضحة أدناه -
| لون | اكتب | أصل |
| بني | سيارات الدفع الرباعي | مستورد |
وبالتالي ، من الصيغة المذكورة أعلاه ، يمكننا حساب الاحتمالات اللاحقة كما هو موضح أدناه -
P (نعم | X) = P (بني | نعم) * P (SUV | نعم) * P (مستورد | نعم) * P (نعم)
= 2/5 * 2/4 * 2/5 * 1
= 0.08
P (لا | X) = P (بني | لا) * P (SUV | لا) * P (مستورد | لا) * P (لا)
= 3/5 * 2/4 * 3/5 * 1
= 0.18
من القيم المحسوبة أعلاه ، نظرًا لأن الاحتمالات الخلفية لـ "لا" أكبر من نعم (0.18> 0.08) ، يمكن الاستدلال على أن السيارة ذات اللون البني ونوع السيارة الرياضية متعددة الاستخدامات من أصل مستورد مصنفة على أنها "لا". ومن ثم فإن السيارة لم تتم سرقتها.
التنفيذ في بايثون
الآن بعد أن فهمنا الرياضيات الكامنة وراء خوارزمية Naive Bayes وتصورها أيضًا بمثال ، دعنا ننتقل إلى كود التعلم الآلي الخاص بها بلغة Python.
ذات صلة: مصنف بايز ساذج
تحليل المشكلة
من أجل تنفيذ برنامج تصنيف Naive Bayes في التعلم الآلي باستخدام Python ، سنستخدم "مجموعة بيانات زهرة القزحية" الشهيرة جدًا. مجموعة بيانات زهرة Iris أو مجموعة بيانات Fisher's Iris هي مجموعة بيانات متعددة المتغيرات قدمها الإحصائي البريطاني وعالم تحسين النسل وعالم الأحياء رونالد فيشر في عام 1998. هذه مجموعة بيانات أساسية صغيرة جدًا تتكون من بيانات رقمية أقل جدًا تحتوي على معلومات حول 3 فئات من الزهور التي تنتمي إلى أنواع السوسن والتي هي -
- ايريس سيتوسا
- آيريس فيرسيكولور
- ايريس فيرجينيكا
هناك 50 عينة من كل نوع من الأنواع الثلاثة تصل إلى مجموعة بيانات إجمالية تتكون من 150 صفًا. السمات الأربعة (أو) المتغيرات المستقلة المستخدمة في مجموعة البيانات هذه هي -
- طول sepal في سم
- عرض سبال في سم
- طول البتلة في سم
- عرض البتلة في سم
المتغير التابع هو " أنواع " الزهرة التي تم تحديدها من خلال السمات الأربع المذكورة أعلاه.
الخطوة 1 - استيراد المكتبات
كما هو الحال دائمًا ، ستكون الخطوة الأساسية في بناء أي نموذج من نماذج التعلم الآلي هي استيراد المكتبات ذات الصلة. لهذا ، سنقوم بتحميل مكتبات NumPy و Mathplotlib و Pandas للمعالجة المسبقة للبيانات.
استيراد numpy كـ np
استيراد matplotlib.pyplot كـ PLT
استيراد الباندا كما pd
الخطوة 2 - تحميل مجموعة البيانات
يجب تحميل مجموعة بيانات زهرة القزحية التي سيتم استخدامها لتدريب مصنف Naive Bayes في إطار بيانات Pandas. يجب تعيين المتغيرات المستقلة الأربعة للمتغير X والمتغير النهائي لأنواع المخرجات يتم تخصيصه لـ y.
dataset = pd.read_csv (' https://raw.githubusercontent.com/mk-gurucharan/Classification/master/IrisDataset.csv' ) X = dataset.iloc [:،: 4] .values
y = مجموعة البيانات ["الأنواع"]. قيمdataset.head (5) >>
sepal_length sepal_width بتلة_الطول أنواع عرض البتلة
5.1 3.5 1.4 0.2 سيتوسا
4.9 3.0 1.4 0.2 سيتوسا
4.7 3.2 1.3 0.2 سيتوسا
4.6 3.1 1.5 0.2 سيتوسا
5.0 3.6 1.4 0.2 سيتوسا
الخطوة 3 - تقسيم مجموعة البيانات إلى مجموعة التدريب ومجموعة الاختبار
بعد تحميل مجموعة البيانات والمتغيرات ، فإن الخطوة التالية هي إعداد المتغيرات التي ستخضع لعملية التدريب. في هذه الخطوة ، يتعين علينا تقسيم المتغيرين X و y للتدريب ومجموعات بيانات الاختبار. لهذا الغرض ، سنخصص 80٪ من البيانات بشكل عشوائي لمجموعة التدريب التي سيتم استخدامها لأغراض التدريب و 20٪ المتبقية من البيانات كمجموعة اختبار يتم على أساسها اختبار مصنف Naive Bayes المدربين للتأكد من دقتها.
من sklearn.model_selection استيراد train_test_split
X_train ، X_test ، y_train ، y_test = train_test_split (X ، y ، test_size = 0.2)
الخطوة 4 - ميزة التحجيم
على الرغم من أن هذه عملية إضافية لمجموعة البيانات الصغيرة هذه ، إلا أنني أضفتها لك لاستخدامها في مجموعة بيانات أكبر. في هذا ، يتم تصغير البيانات الموجودة في مجموعات التدريب والاختبار إلى نطاق من القيم بين 0 و 1. وهذا يقلل من التكلفة الحسابية.
من sklearn.preprocessing استيراد StandardScaler
sc = StandardScaler ()
X_train = sc.fit_transform (X_train)
X_test = sc.transform (X_test)
الخطوة 5 - تدريب نموذج تصنيف Naive Bayes على مجموعة التدريب
في هذه الخطوة نقوم باستيراد فئة Naive Bayes من مكتبة sklearn. بالنسبة لهذا النموذج ، نستخدم نموذج Gaussian ، وهناك العديد من النماذج الأخرى مثل Bernoulli و Categorical و Multinomial. وبالتالي ، يتم تركيب X_train و y_train مع متغير المصنف لغرض التدريب.
من sklearn.naive_bayes استيراد GaussianNB
المصنف = GaussianNB ()
classifier.fit (X_train ، y_train)
الخطوة 6 - توقع نتائج مجموعة الاختبار -
نتوقع فئة الأنواع لمجموعة الاختبار باستخدام النموذج المدرب ومقارنته بالقيم الحقيقية لفئة الأنواع.
y_pred = classifier.predict (X_test)
df = pd.DataFrame ({'Real Values': y_test، 'Predicted Values': y_pred})
مدافع >>
القيم الحقيقية والقيم المتوقعة
سيتوسا سيتوسا
سيتوسا سيتوسا
فيرجينيكا فيرجينيكا
المبرقشة المبرقشة
سيتوسا سيتوسا
سيتوسا سيتوسا
……………
فيرجينيكا المبرقشة
فيرجينيكا فيرجينيكا
سيتوسا سيتوسا
سيتوسا سيتوسا
المبرقشة المبرقشة
المبرقشة المبرقشة
في المقارنة أعلاه ، نرى أن هناك تنبؤًا واحدًا غير صحيح تنبأ بالبرسيكولور بدلاً من فيرجينيكا.
الخطوة 7 - مصفوفة الارتباك والدقة
نظرًا لأننا نتعامل مع التصنيف ، فإن أفضل طريقة لتقييم نموذج المصنف لدينا هي طباعة مصفوفة الارتباك جنبًا إلى جنب مع دقتها على مجموعة الاختبار.
من sklearn.metrics استيراد confusion_matrix
cm = confusion_matrix (y_test، y_pred) من sklearn.metrics دقة الاستيراد

print ("Accuracy:"، freedom_score (y_test، y_pred))
سم >> الدقة: 0.9666666666666667
>> صفيف ([[14 ، 0 ، 0] ،
[0 ، 7 ، 0] ،
[0 ، 1 ، 8]])
خاتمة
وهكذا ، في هذه المقالة ، راجعنا أساسيات خوارزمية Naive Bayes ، وفهمنا الرياضيات الكامنة وراء التصنيف جنبًا إلى جنب مع مثال تم حله يدويًا. أخيرًا ، قمنا بتنفيذ رمز التعلم الآلي لحل مجموعة بيانات شائعة باستخدام خوارزمية تصنيف Naive Bayes.
إذا كنت مهتمًا بمعرفة المزيد عن الذكاء الاصطناعي والتعلم الآلي ، فراجع IIIT-B & upGrad's دبلوم PG في التعلم الآلي والذكاء الاصطناعي المصمم للمهنيين العاملين ويقدم أكثر من 450 ساعة من التدريب الصارم ، وأكثر من 30 دراسة حالة ومهمة ، حالة خريجي IIIT-B ، أكثر من 5 مشاريع تكميلية عملية ومساعدة وظيفية مع أفضل الشركات.
كيف يكون الاحتمال مفيدًا في التعلم الآلي؟
قد نضطر إلى اتخاذ قرارات بناءً على معلومات جزئية أو غير كاملة في سيناريوهات العالم الحقيقي. يساعدنا الاحتمال على تحديد أوجه عدم اليقين في مثل هذه الأنظمة وإدارة مخاطر المهمة. تعمل الطريقة التقليدية فقط من أجل النتائج الحتمية لإجراءات محددة ، ولكن هناك دائمًا نطاق معين من عدم اليقين في أي نموذج تنبؤ. يمكن أن يأتي عدم اليقين هذا من العديد من المعلمات من بيانات الإدخال ، مثل الضوضاء في البيانات. أيضًا ، يمكن أن تساعد وجهات النظر البايزية من نظريات الاحتمال في التعرف على الأنماط من بيانات الإدخال. لهذا ، يستخدم الاحتمال مفهوم تقدير الاحتمالية القصوى ، وبالتالي فهو مفيد في إنتاج النتائج ذات الصلة.
ما فائدة مصفوفة الارتباك؟
مصفوفة الارتباك هي مصفوفة 2 × 2 تستخدم لتفسير أداء نموذج التصنيف. يجب أن تكون القيم الحقيقية لبيانات الإدخال معروفة حتى يعمل هذا ، لذلك لا يمكن تمثيلها للبيانات غير المسماة. يتكون من عدد الإيجابيات الكاذبة (FP) والإيجابيات الحقيقية (TP) والسلبيات الكاذبة (FN) والسلبيات الحقيقية (TN). يتم تصنيف التنبؤات في هذه الفئات باستخدام العد من مجموعة التدريب ومجموعة الاختبار. يساعدنا في تصور المعلمات المفيدة مثل الدقة والدقة والاستدعاء والخصوصية. إنه سهل الفهم نسبيًا ويمنحك فكرة واضحة عن الخوارزمية.
ما هي الأنواع المختلفة لنموذج Naive Bayes؟
تعتمد جميع الأنواع أساسًا على نظرية بايز. يحتوي نموذج Naive Bayes بشكل عام على ثلاثة أنواع: Gaussian و Bernoulli و Multinomial. يساعد Gaussian Naive Bayes في القيم المستمرة من معلمات الإدخال ، ويفترض أن جميع فئات بيانات الإدخال موزعة بشكل موحد. يعتبر Bayes الساذج من Bernoulli نموذجًا قائمًا على الحدث حيث تكون ميزات البيانات مستقلة وموجودة في القيم المنطقية. تعتمد Multinomial Naive Bayes أيضًا على نموذج قائم على الحدث. يحتوي على ميزات البيانات في شكل متجه ، والتي تمثل الترددات ذات الصلة بناءً على حدوث الأحداث.
