مقدمة إلى دالة كثافة الاحتمال [صيغة ، خصائص ، تطبيقات ، أمثلة]

دالة الكثافة الاحتمالية (PDF) هي تعبير في الإحصائيات يشير إلى التوزيع الاحتمالي لمتغير عشوائي منفصل. يمكن تعريف التوزيع الاحتمالي ، بعبارات بسيطة ، على أنه احتمال نتيجة متغير عشوائي مثل الأسهم أو صناديق الاستثمار المتداولة. تحدث المتغيرات المنفصلة على عكس المتغير العشوائي المستمر الذي يمكن تحديد قيمته الدقيقة.

على سبيل المثال ، تحتوي قيمة السهم في سوق الأوراق المالية على نقطتين عشريتين فقط (على سبيل المثال ، 65.76) في متغير عشوائي منفصل بدلاً من المتغير المستمر مع أي عدد من النقاط العشرية (مثال: 65.7685434567).

دالة كثافة الاحتمال هي أداة إحصائية تُستخدم لتحديد احتمالية نتيجة متغير عشوائي منفصل. عند رسمها على الرسم البياني ، تبدو ملفات PDF متطابقة مع منحنى الجرس حيث تمثل المنطقة الواقعة أسفل المنحنى احتمال النتيجة.

عند الإسقاط كنموذج رسومي ، تمثل المنطقة الواقعة أسفل المنحنى النطاق الذي ستقع فيه قيم المتغيرات العشوائية المنفصلة. وبالتالي ، فإن المساحة الإجمالية تحت المنحنى تساوي احتمال نتيجة المتغير.

يمكن أن تحدد دالة كثافة الاحتمال احتمالية وقوع متغير عشوائي ضمن نطاق معين من القيم.

عادةً ما تقوم وظائف كثافة الاحتمالات بتحليل المخاطر والإيرادات المحتملة المرتبطة بصندوق معين في سوق الأوراق المالية.

الشروط التي يجب استيفاءها بواسطة دالة يتم اعتبارها دالة كثافة احتمالية

يمكن قياس قيمة المتغير المنفصل بدقة على عكس المتغير المستمر الذي يمكن أن يكون له عدد لا حصر له من القيم. يجب أن تفي أي دالة بالشرطين التاليين لتكون دالة كثافة احتمالية:

• يجب أن تكون قيمة f (x) لكل قيمة محتملة للمتغير العشوائي موجبة (غير سالبة).
• يجب أن تكون القيمة التكاملية للمساحة الإجمالية للمنحنى (وهي جزء لا يتجزأ من جميع القيم الممكنة للمتغير العشوائي) 1.

الفرق بين دالة الكثافة الاحتمالية ووظيفة التوزيع الاحتمالي

يمكن أن تحتوي المتغيرات العشوائية على العديد من القيم. يسمى وصف كل قيمة محتملة يمكن أن يمتلكها متغير عشوائي التوزيع الاحتمالي الخاص به.

يعطي توزيع الاحتمالات مجموعة من النتائج والاحتمالات المرتبطة بها. تُعرف الوظيفة الإحصائية التي تمثل توزيعًا احتماليًا مستمرًا باسم دالة كثافة الاحتمال.

هناك أداة إحصائية أخرى تمثل توزيع احتمالي منفصل يسمى دالة كتلة الاحتمال. يقدم هذا سردًا مفصلاً لجميع النتائج المحتملة واحتمالات الاحتمالية الخاصة بها.

التعبير عن دالات الكثافة الاحتمالية

إذا كان المتغير العشوائي منفصلاً ، فإن توزيعه الاحتمالي يسمى دالة كتلة الاحتمال ، وإذا كان متغيرًا مستمرًا ، فإن توزيع الاحتمال يسمى دالة كثافة الاحتمال.

يتم استخدام PDF عندما يكون للمتغير العشوائي المعني نطاق من القيم الممكنة. يتم استخدام توزيع الاحتمالات الخاص بهم لتحديد القيمة الدقيقة.

دع المتغير العشوائي يُرمز إليه بـ X. يمكن التعبير عن دالة كثافة الاحتمال ، f للمتغير العشوائي X كـ

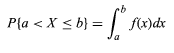
• تقع قيمة المتغير العشوائي بين a و b.
• إذا كانت X تشير إلى احتمال اختيار رقم معين من النطاق (الفاصل) r و s ، فيمكن التعبير عن دالة كثافة الاحتمال على النحو التالي

f ( x ) = 1 / ( s - r ) لـ r < x < s و f ( x ) = 0 لـ x < r أو x > s .

• يتم تمثيل ملف PDF F على النحو التالي:

و ( س ) = ف { س ≤ س }

والتي تسمى دالة التوزيع أو دالة التوزيع التراكمي لـ X.

بالنظر إلى المتغير العشوائي X لديه دالة توزيع احتمالية f ( x ) ، ثم يمكن إنشاء العلاقة بين f و F

و ′ (. س ) = و ( س )

تختلف دالة توزيع المتغير العشوائي المنفصل عن دالة التوزيع الاحتمالي. يمكن التعبير عن العلاقة بين الاثنين على النحو التالي:

يُشار إلى توقع المتغير العشوائي على أنه ،

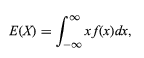
وبالتالي ، يمكن معالجة جميع المتغيرات المنفصلة والعشوائية بشكل موحد بمساعدة نظرية مشتركة.

صيغة دالة الكثافة الاحتمالية

دائمًا ما يكون احتمال وجود متغير عشوائي X مستمر على قيمة ثابتة x هو 0. في هذه الحالة ، لا يمكن استخدام P (X = x). يجب تحديد قيمة X الواقعة بين نطاق من القيم (أ ، ب). لتحديد نفس الشيء ، يتم استخدام الصيغة التالية.

خصائص دالة الكثافة الاحتمالية

المتغير العشوائي المستمر الذي يأخذ قيمته بين النطاق (أ ، ب) ، على سبيل المثال ، سيتم تقديره عن طريق حساب المنطقة الواقعة أسفل المنحنى والمحور X مرسومًا بـ (أ) باعتباره الحد الأدنى و (ب) كحسابه الحد الأعلى. يتم تمثيل دالة كثافة الاحتمال لما سبق على النحو التالي:

دالة كثافة الاحتمال موجبة (غير سالبة) لجميع القيم الممكنة. هذا يعني f (x) ≥ 0 لكل x. المساحة الواقعة بين منحنى الكثافة والمحور السيني (المحور الأفقي) تساوي 1.

يمكن أيضًا الإشارة إلى هذا على النحو التالي:

منحنى دالة الكثافة مستمر في جميع أنحاء النطاق المحدد ، والذي يتم تعريفه بوضوح مقابل سلسلة من القيم المستمرة أو مجال المتغير.

انضم إلى دورة التعلم الآلي عبر الإنترنت من أفضل الجامعات في العالم - الماجستير ، وبرامج الدراسات العليا التنفيذية ، وبرنامج الشهادات المتقدمة في ML & AI لتسريع حياتك المهنية.

تطبيقات دالة الكثافة الاحتمالية

• تُستخدم دالة كثافة الاحتمال في النمذجة السنوية لمستويات تركيز NO في الغلاف الجوي.
• نمذجة احتراق محرك الديزل.
• في الإحصاء ، تُستخدم دالة كثافة الاحتمال لتحديد احتمالات نتيجة متغير عشوائي.

أمثلة على دالة الكثافة الاحتمالية

• مثال 1

فيما يلي مثال على كيفية استخدام دالة كثافة الاحتمال (PDF) لتحديد المخاطر المحتملة للمستثمر في سوق الأوراق المالية:

أولاً ، يتم إنشاء ملفات PDF كأداة رسومية بناءً على المعلومات التاريخية.

الشكل الأكثر شيوعًا لملفات PDF هو الإسقاط المحايد ، حيث تكون المخاطرة مساوية للمكافأة عبر مجموعة من الاحتمالات. سيكافأ المستثمرون ذوو القدرة الأقل على المخاطرة فقط بأرباح محدودة ، وبالتالي يقعون تحت الجانب الأيسر من منحنى الجرس. على العكس من ذلك ، من المرجح أن يكافأ المستثمرون الذين يتمتعون بقدرات عالية على المخاطرة بعائدات أعلى ، وبالتالي يقعون تحت الجانب الأيمن من المنحنى.

يقع معظم المستثمرين تحت متوسط ​​القدرة على المخاطرة ، وبالتالي يشغلون منتصف المنحنى.

يساعد ذلك في تحليل فئة المستثمرين بناءً على البيانات الواردة. يساعد هذا وسطاء سوق الأوراق المالية على تحديد الفئة المستهدفة من العملاء لبيع منتجاتهم.

• مثال 2

أحد التطبيقات الأساسية لوظيفة كثافة الاحتمال هو المتغير العشوائي الغاوسي ، المعروف أيضًا باسم المتغير العشوائي العادي.

في كلتا الحالتين ، يعطي الرسم البياني منحنى جرس لدالة كثافة الاحتمال.

يمكن التعبير عن الكثافة كـ

الرسم البياني لمعادلة الكثافة أعلاه معطى أدناه.

تمثل المنطقة الواقعة أسفل المنحنى القيمة الفعلية للمتغير العشوائي الغاوسي.

خاتمة

تلعب دالة كثافة الاحتمال دورًا حيويًا في التعلم الآلي. للطلاب الذين يتطلعون إلى الحصول على وظيفة في التعلم الآلي والذكاء الاصطناعي ، نوصي بشدة بالتسجيل في برنامج upGrad's IIT المتقدم لشهادة التعلم الآلي . تم تخصيص البرنامج وتصميمه لتزويد كبار المهنيين العاملين لنشر نماذج التعلم الآلي باستخدام تكنولوجيا الحوسبة السحابية.

تم تصميم المنهج من قبل أعضاء هيئة التدريس من IIT Madras وخبراء الصناعة لجعل عملية التعلم أكثر صلة وعملية. يقدم البرنامج شهادة معترف بها عالميًا من كلية الهندسة المرغوبة والمرتبة رقم 1 في الهند ودعم تحديد المستوى 360 درجة من upGrad.

علاوة على ذلك ، تحصل على العديد من الفرص للتعاون في مشاريع واسعة النطاق مع قاعدة المتعلمين المدفوعة في upGrad التي تزيد عن 40.000.

توجه إلى موقعنا لبدء رحلة التعلم الخاصة بك!