العثور على ثالث أصغر رقم في جافا: دليل كامل

هل تساءلت يومًا عن كيفية العثور على ثالث أصغر رقم بكفاءة في مصفوفة أو قائمة أو مجموعة من الأعداد الصحيحة؟ في منشور المدونة هذا، سنتعمق في عالم برمجة Java ونستكشف تقنيات مختلفة لتحديد ثالث أصغر رقم في مصادر البيانات المختلفة.

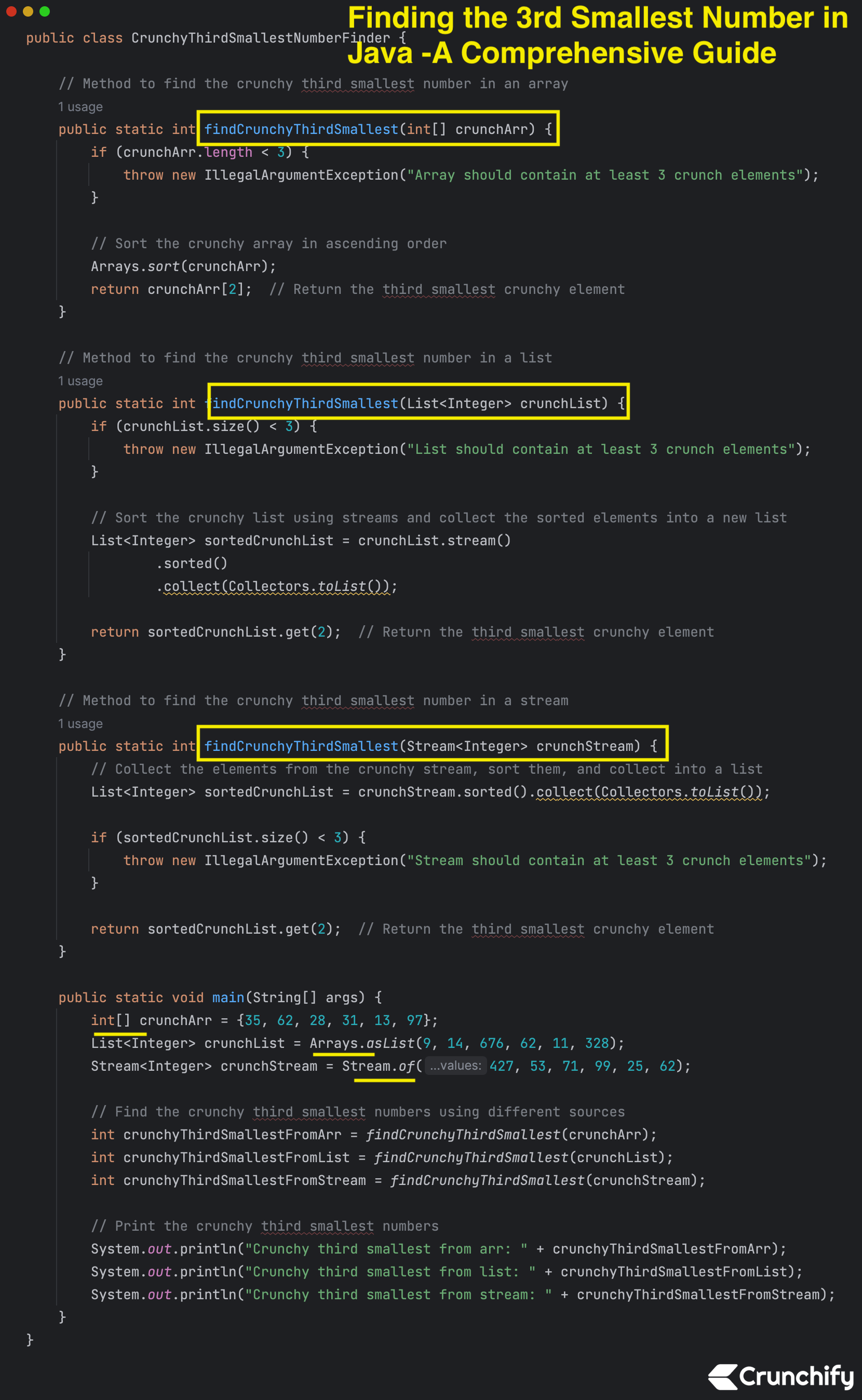
عند العمل مع معالجة البيانات وتحليلها، غالبًا ما تنشأ الحاجة إلى تحديد عناصر محددة ضمن مجموعة من الأرقام. يعد العثور على أصغر أو أكبر رقم أمرًا بسيطًا نسبيًا، لكن تحديد ثالث أصغر رقم يتطلب المزيد من الدقة. في منشور المدونة هذا، سنغطي ثلاث طرق لمعالجة هذه المشكلة باستخدام Java: فرز مصفوفة، وفرز قائمة، واستخدام التدفقات.

الطريقة الأولى: فرز صفيف

المصفوفات هي إحدى هياكل البيانات الأساسية في Java، مما يجعلها نقطة انطلاق طبيعية لاستكشافنا. الفكرة هنا هي فرز المصفوفة بترتيب تصاعدي ثم استرداد العنصر الموجود في الفهرس 2.

الطريقة الثانية: فرز القائمة

توفر القوائم بديلاً أكثر مرونة للمصفوفات، مما يسمح بتغيير الحجم الديناميكي وسهولة المعالجة. للعثور على ثالث أصغر رقم في القائمة، يمكننا اتباع طريقة مماثلة لفرز المصفوفات.

الطريقة الثالثة: استخدام التدفقات

تعد تدفقات Java طريقة فعالة لمعالجة تسلسل العناصر. يمكننا استخدام التدفقات لفرز العناصر ثم استرجاع ثالث أصغر رقم.

اختيار الطريقة الصحيحة

كل طريقة لها مزاياها وحالات الاستخدام الخاصة بها. إذا كان لديك مصفوفة في متناول اليد، فقد تكون طريقة فرز المصفوفة هي الأكثر كفاءة. تتميز القوائم بأنها متعددة الاستخدامات وتوفر مزيدًا من الراحة، بينما توفر التدفقات أسلوبًا وظيفيًا ويمكنها التعامل مع مجموعات البيانات الأكبر حجمًا بسهولة.

هنا مثال كامل:

CrunchyThirdSmallestNumberFinder.java

 الحزمة Crunchify.com.tutorial؛

استيراد java.util.Arrays؛
import java.util.List;
import java.util.stream.Collectors;
import java.util.stream.Stream;

/**
 * @author Crunchify.com
 * العثور على ثالث أصغر رقم في جافا: دليل شامل
 *
 */

الطبقة العامة CrunchyThirdSmallestNumberFinder {

    // طريقة للعثور على ثالث أصغر رقم مقرمش في مصفوفة
    public static int findCrunchyThirdSmallest(int[] crunchArr) {
        إذا (crunchArr.length < 3) {
            throw new IllegalArgumentException("يجب أن يحتوي الصفيف على 3 عناصر أزمة على الأقل");
        }

        // قم بفرز المصفوفة المقرمشة بترتيب تصاعدي
        Arrays.sort(crunchArr);
        إرجاع CrunchArr[2]; // إرجاع ثالث أصغر عنصر مقرمش
    }

    // طريقة للعثور على ثالث أصغر رقم مقرمش في القائمة
    public static int findCrunchyThirdSmallest(List<Integer> crunchList) {
        إذا (crunchList.size() < 3) {
            throw new IllegalArgumentException("يجب أن تحتوي القائمة على 3 عناصر أزمة على الأقل");
        }

        // قم بفرز القائمة المقرمشة باستخدام التدفقات وجمع العناصر التي تم فرزها في قائمة جديدة
        قائمة<عدد صحيح> تم فرزهاCrunchList = crunchList.stream()
                .مرتبة()
                .collect(Collectors.toList());

        إرجاعsortedCrunchList.get(2); // إرجاع ثالث أصغر عنصر مقرمش
    }

    // طريقة للعثور على ثالث أصغر رقم مقرمش في الدفق
    public static int findCrunchyThirdSmallest(Stream<Integer> crunchStream) {
        // جمع العناصر من الدفق المقرمش، وفرزها، وجمعها في القائمة
        List<Integer>sortedCrunchList = crunchStream.sorted().collect(Collectors.toList());

        إذا (sortedCrunchList.size() < 3) {
            throw new IllegalArgumentException("يجب أن يحتوي الدفق على 3 عناصر أزمة على الأقل");
        }

        إرجاعsortedCrunchList.get(2); // إرجاع ثالث أصغر عنصر مقرمش
    }

    public static void main(String[] args) {
        int[] crunchArr = {35, 62, 28, 31, 13, 97};
        List<Integer> crunchList = Arrays.asList(9, 14, 676, 62, 11, 328);
        Stream<Integer> crunchStream = Stream.of(427, 53, 71, 99, 25, 62);

        // ابحث عن ثالث أصغر الأرقام المقرمشة باستخدام مصادر مختلفة
        int crunchyThirdSmallestFromArr = findCrunchyThirdSmallest(crunchArr);
        int crunchyThirdSmallestFromList = findCrunchyThirdSmallest(crunchList);
        int crunchyThirdSmallestFromStream = findCrunchyThirdSmallest(crunchStream);

        // اطبع ثالث أصغر الأرقام المقرمشة
        System.out.println("ثالث أصغر مقرمش من arr: " + crunchyThirdSmallestFromArr);
        System.out.println("ثالث أصغر مقرمش من القائمة: " + crunchyThirdSmallestFromList);
        System.out.println("ثالث أصغر مقرمش من الدفق:" + crunchyThirdSmallestFromStream);
    }
}

نتيجة وحدة تحكم Eclipse:

ما عليك سوى تشغيل البرنامج أعلاه في Eclipse IDE أو IntelliJ IDEA وستكون النتيجة على النحو التالي.

 كرانشي ثالث أصغر من arr: 31
مقرمش ثالث أصغر من القائمة: 14
مقدد ثالث أصغر من التيار: 62

انتهت العملية برمز الخروج 0

هناك بعض الاختلافات في الأداء التي يجب مراعاتها:

فيما يتعلق بالتعقيد الزمني، فإن جميع الطرق الثلاث لها خطوات فرز متشابهة، والتي عادةً ما يكون لها تعقيد زمني قدره O(n log n) ، حيث 'n' هو عدد العناصر في المجموعة (مصفوفة أو قائمة أو دفق).

التعقيد الزمني للوصول إلى ثالث أصغر عنصر ثابت، O(1) ، نظرًا لأنه عبارة عن مصفوفة بسيطة أو قائمة بحث.

1. طريقة المصفوفة: تقوم هذه الطريقة بفرز المصفوفة في مكانها، بحيث لا تتطلب ذاكرة إضافية لمجموعة مفروزة جديدة. يمكن أن يؤدي هذا إلى استخدام ذاكرة أفضل قليلاً مقارنة بأساليب القائمة والدفق.
2. طريقة القائمة: تقوم هذه الطريقة بتحويل القائمة إلى قائمة مرتبة باستخدام التدفقات. على الرغم من أنه مناسب، إلا أنه يتضمن إنشاء قائمة جديدة، مما يستهلك ذاكرة إضافية. قد يكون هذا مصدر قلق إذا كان استخدام الذاكرة أمرًا بالغ الأهمية.
3. طريقة الدفق: طريقة الدفق مرنة وعملية للغاية، ولكنها تتضمن تجميع الدفق في قائمة. وهذا يضيف حملًا صغيرًا من حيث الذاكرة والمعالجة مقارنةً بفرز المصفوفة مباشرةً.

اسمحوا لي أن أعرف إذا كنت تواجه أي مشكلة في تشغيل هذا الرمز.