ترقية الرسوم المتحركة لـ CSS باستخدام منحنيات الحركة

هناك رسوم متحركة لواجهة المستخدم ، ثم هناك رسوم متحركة جيدة لواجهة المستخدم. الرسوم المتحركة الجيدة تجعلك تذهب "واو!" - إنها سلسة وجميلة والأهم من ذلك كله طبيعية وليست ممتلئة أو صلبة أو آلية. إذا كنت متكررًا Dribbble أو UpLabs ، فستعرف ما أتحدث عنه.

مزيد من القراءة عن التحطيم:

• الرسوم المتحركة SVG و CSS مع مسار القصاصة
• تقنيات الرسوم المتحركة العملية
• إنشاء رسوم متحركة "مرسومة باليد" باستخدام SVG
• واجهة برمجة تطبيقات Web Animation الجديدة

مع وجود العديد من المصممين المذهلين الذين يقومون بإنشاء مثل هذه الرسوم المتحركة الجميلة ، فإن أي مطور يرغب بطبيعة الحال في إعادة إنشائها في مشاريعه الخاصة. الآن ، توفر CSS بعض الإعدادات المسبقة transition-timing-function ، مثل ease-in ease-out ease-in-out ، والتي تضيف مستوى معينًا من السلاسة والواقعية ، لكنها عامة جدًا ، أليس كذلك؟ كم سيكون مملاً إذا اتبعت كل الرسوم المتحركة على الويب وظائف التوقيت الثلاث نفسها؟

إحدى خصائص transition-timing-function هي cubic-bezier(n1, n2, n3, n4) ، حيث يمكنك تمرير أربعة أرقام لإنشاء دالة التوقيت الخاصة بك. قرب نهاية هذا المقال ، ستعرف بالضبط ما تمثله هذه الأرقام الأربعة - ومع ذلك ، صدقني ، فإن الخروج بأربعة أرقام لالتقاط الانتقال الذي تتخيله في رأسك ليس قريبًا من أن يكون سهلاً. لكن بفضل cubic-bezier وقيصر ، لست مضطرًا لذلك. تجلب هذه الأدوات منحنيات الحركة إلى الويب.

يتم استخدام منحنيات الحركة بشكل أساسي بواسطة الرسوم المتحركة (على سبيل المثال ، في Adobe After Effects) لإنشاء رسوم متحركة متقدمة وواقعية. باستخدام cubic-bezier و Ceasar ، يمكنك ببساطة معالجة شكل المنحنى ، وسيتم ملء هذه الأرقام الأربعة ( n1, n2, n3, n4 ) من أجلك ، وهو أمر رائع للغاية! ومع ذلك ، لاستخدام منحنيات الحركة والاستفادة منها إلى أقصى حد ، تحتاج إلى فهم كيفية عملها ، وهذا ما سنفعله في هذه المقالة. هيا نبدأ.

فهم منحنيات الحركة

منحنى الحركة ليس سوى قطعة أرض بين أي خاصية متحركة ووقت. يحدد منحنى الحركة كيف تختلف سرعة الرسوم المتحركة التي تعمل تحت تأثيرها بمرور الوقت.

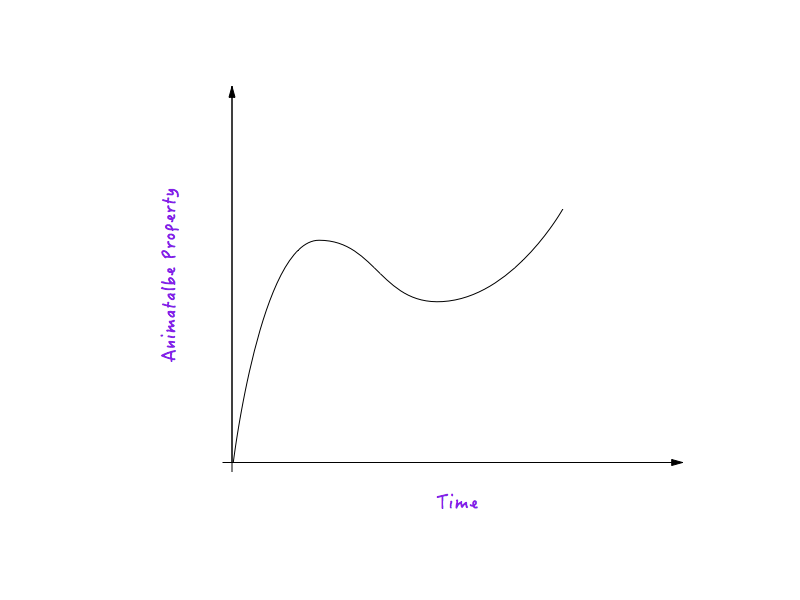
لنأخذ المسافة ( translateX ) كمثال على خاصية متحركة. (الشرح ينطبق على أي خاصية متحركة أخرى.)

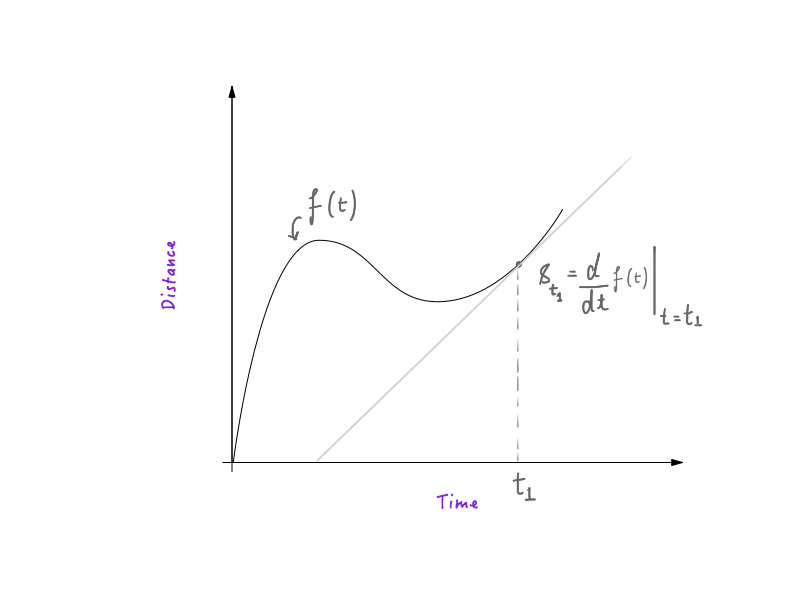
إذا كان لديك أي خبرة في الفيزياء وحساب التفاضل والتكامل الأساسي ، فستعرف أن فك شفرة السرعة من الرسم البياني للوقت والمسافة أمر بسيط للغاية. أول مشتق للمسافة كدالة للوقت ، فيما يتعلق بالوقت ، هو السرعة ، مما يعني أن الكائن الذي يتبع منحنى المسافة والوقت سيكون له سرعة أكبر في الأماكن التي يكون فيها المنحنى حادًا ومنخفضًا في الأماكن التي يكون فيها المنحنى أكثر انبساطًا . إذا كنت تعرف كيف يعمل هذا ، عظيم! أنت جاهز تمامًا ويمكنك الانتقال إلى القسم التالي.

الآن ، أدرك أن التصميم والتطوير مجال متنوع ، وليس كل شخص لديه نفس الخلفية. ربما كانت الفقرتان المذكورتان أعلاه مصطلحات لك. لا تأكل. سنواصل المضي قدمًا ونفهم المصطلحات.

ضع في اعتبارك المربع الأحمر أدناه. دعنا نحصل على القليل من الصلابة هنا وندعو الصندوق الأحمر "Boxy" ؛ سيكون من الأسهل الرجوع إليها بهذه الطريقة. حسنًا ، سوف ينتقل Boxy من حافة الشاشة إلى الأخرى بطريقة خطية ، وسنقوم بتحليل حركته.

أحد الإعدادات المسبقة transition-timing-function linear . لجعل Boxy يتحرك ، كل ما نقوم به هو إضافة الفصل التالي.

 .moveForward { transform: translateX(1000px); }

للتحكم في الرسوم المتحركة ، سنقوم بتعيين خاصية transition لـ Boxy على النحو التالي:

 #boxy { width: 200px; height: 200px; background: red; transition-property: transform; transition-duration: 1s; transition-timing-function: linear; }

هذه طريقة مسهبة للغاية لتحديد transition . في الواقع ، ستجد دائمًا transition مكتوبًا في شكله المختصر:

 #boxy { width: 200px; height: 200px; background: red; transition: transform 1s linear; }

دعونا نرى الأمر.

الروبوتية ، أليس كذلك؟ يمكنك القول أن هذه الحركة تبدو آلية لأنها خطية ، وهي إجابة معقولة تمامًا. لكن هل يمكن أن تشرح لماذا؟ يمكننا أن نرى أن الإعداد linear ينتج عنه حركة آلية ، ولكن ما الذي يحدث بالضبط خلف الكواليس؟ هذا ما سنكتشفه أولاً ؛ سنصل إلى الأجزاء الداخلية ونفهم لماذا تبدو هذه الحركة آلية ومكتلة وغير طبيعية.

لنبدأ برسم حركة Boxy بالرسوم البيانية لمعرفة ما إذا كان بإمكاننا اكتساب بعض البصيرة. يتكون الرسم البياني من محورين ، الأول هو المسافة والثاني. يغطي Boxy مسافة إجمالية قدرها 1000 بكسل (مسافة) في ثانية واحدة (وقت). الآن ، لا تخف من كل العمليات الحسابية أدناه - إنها بسيطة جدًا.

هذا هو رسمنا البياني البسيط للغاية ، مع المحاور كما هو مذكور.

في الوقت الحالي ، إنه فارغ. دعونا نملأه ببعض البيانات.

للبدء ، نعلم أنه في 0 ثانية ، عندما لم تبدأ الرسوم المتحركة بعد ، يكون Boxy في موضعه الأولي (0 بكسل). وبعد مرور ثانية واحدة ، قطع Boxy ما مجموعه 1000 بكسل ، وهبط على الحافة المقابلة للشاشة.

دعونا نرسم هذه البيانات على الرسم البياني.

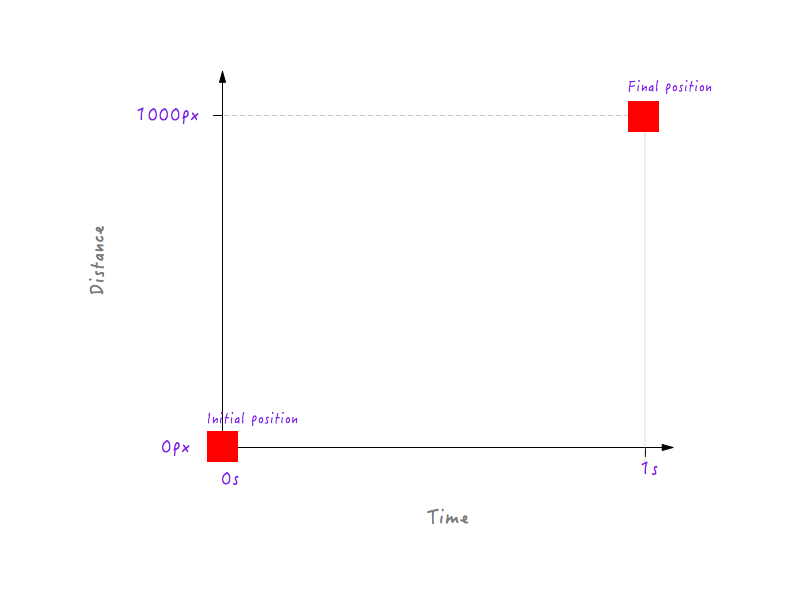
حتى الان جيدة جدا. لكن نقطتي بيانات لا تكفيان - فنحن بحاجة إلى المزيد. يوضح الشكل التالي أوضاع Boxy في نقاط زمنية مختلفة (كل ذلك بفضل الكاميرا عالية السرعة).

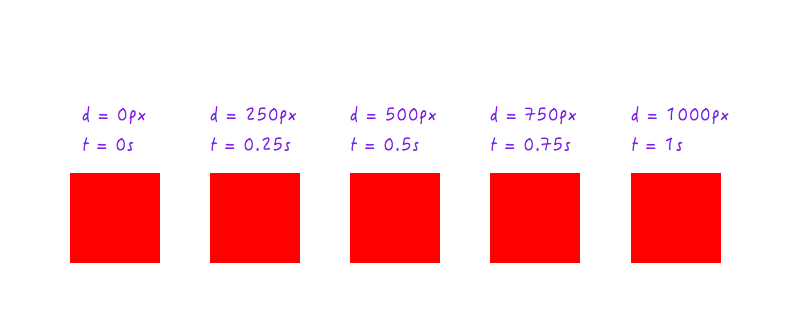
دعنا نضيف هذه البيانات إلى الرسم البياني الخاص بنا.

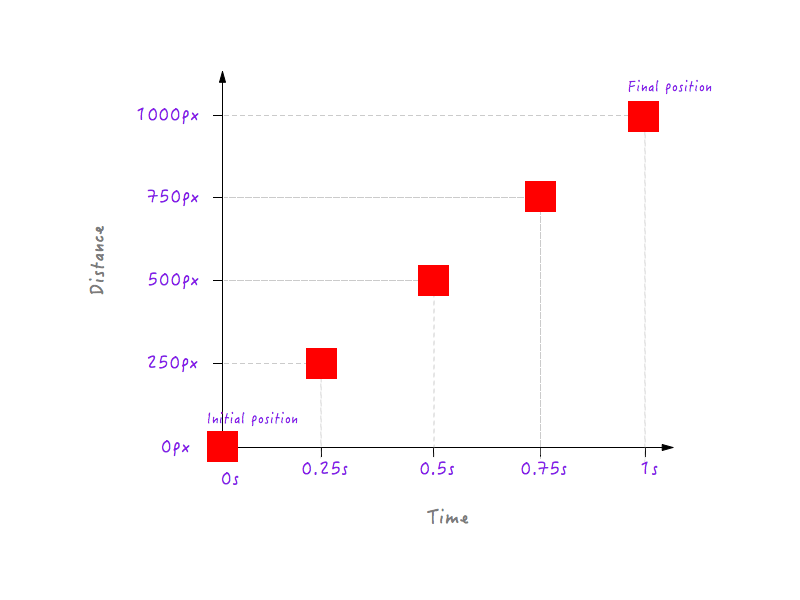
يمكنك بالطبع الحصول على العديد من نقاط البيانات لأوقات مختلفة (على سبيل المثال ، 0.375 ثانية ، 0.6 ثانية ، وما إلى ذلك) ولكن ما لدينا يكفي لإكمال الرسم البياني الخاص بنا. بجمع كل النقاط نكون قد أكملنا الرسم البياني. كفك!

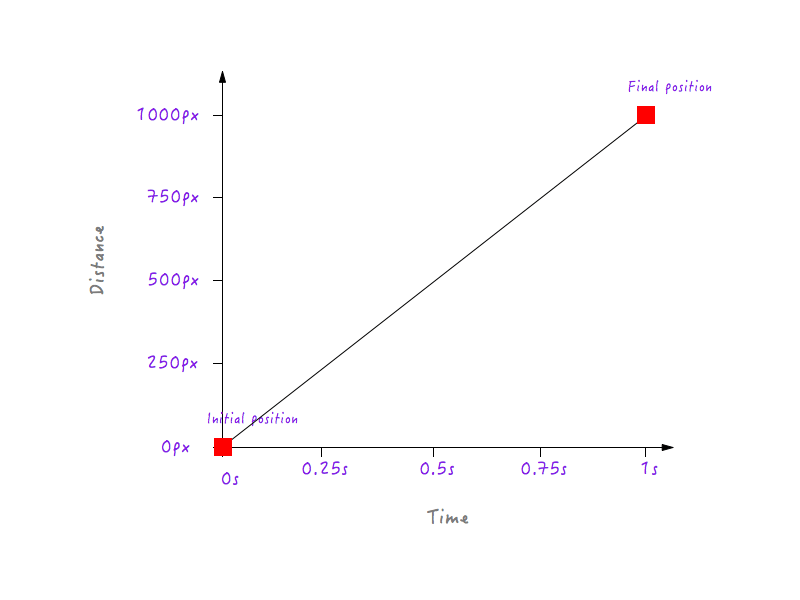
رائع ، لكن ماذا يخبرنا هذا؟ تذكر أننا بدأنا تحقيقنا بهدف فهم لماذا تبدو الحركة الخطية لـ Boxy غير طبيعية وروبوتية؟ في لمحة ، هذا الرسم البياني الذي أنشأناه للتو لا يخبرنا بأي شيء عن ذلك. نحن بحاجة إلى التعمق.

ضع الرسم البياني في اعتبارك ودعنا نتحدث لمدة دقيقة عن السرعة. أعلم أنك تعرف ما هي السرعة - أود فقط أن أصفها بمصطلحات رياضية. معادلة السرعة كما يلي:

لذلك ، إذا قطعت السيارة مسافة 100 كيلومتر في ساعة واحدة ، نقول إن سرعتها 100 كيلومتر في الساعة.

إذا ضاعفت السيارة سرعتها ، فستبدأ في قطع ضعف المسافة (200 كيلومتر) في نفس الفترة (ساعة واحدة) ، أو بمعنى آخر ، ستغطي المسافة الأصلية البالغة 100 كيلومتر في نصف الوقت (0.5 ساعة) . منطقي؟

وبالمثل ، إذا خفضت السيارة سرعتها إلى النصف (أي تباطأت السرعة بمقدار النصف) ، فستبدأ في قطع مسافة 50 كيلومترًا في نفس الفترة (ساعة واحدة) ، أو بعبارة أخرى ، ستغطي المسافة الأصلية البالغة 100 كيلومترات في ضعف الوقت (ساعتان).

رائعة! مع هذا بعيدًا ، دعنا ننتقل من حيث توقفنا. كنا نحاول معرفة كيف يمكن للرسم البياني بين المسافة والوقت أن يساعدنا في فهم لماذا تبدو الحركة الخطية لـ Boxy آلية.

مهلا ، انتظر لحظة! لدينا رسم بياني بين المسافة والوقت ، ويمكن حساب السرعة من المسافة والوقت ، أليس كذلك؟ دعنا نحاول حساب سرعة Boxy على فترات زمنية مختلفة.

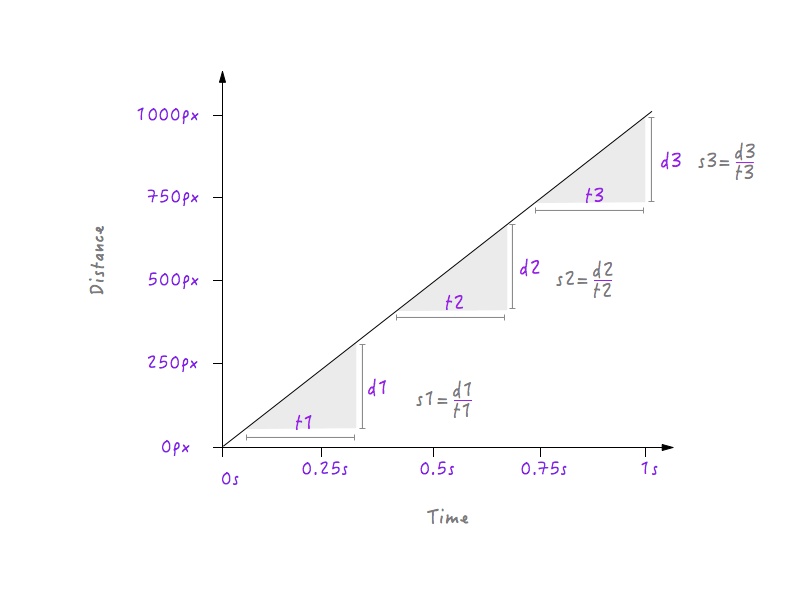
هنا ، اخترت ثلاث فترات زمنية مختلفة: واحدة بالقرب من البداية ، وواحدة في المنتصف وواحدة في النهاية بالقرب من الموضع النهائي. كما هو واضح ، في جميع الفترات الثلاثة ، يمتلك Boxy نفس السرعة (s1 = s2 = s3) وهي 1000 بكسل في الثانية ؛ أي بغض النظر عن الفاصل الزمني الذي تختاره في الرسم البياني أعلاه ، ستجد Boxy يتحرك بسرعة 1000 بكسل في الثانية. أليس هذا غريبا؟ الأشياء في الحياة الواقعية لا تتحرك بسرعة ثابتة ؛ يبدأون ببطء ، ويزيدون سرعتهم تدريجيًا ، ويتحركون لفترة من الوقت ، ثم يبطئون مرة أخرى قبل التوقف ، لكن Boxy يبدأ فجأة بسرعة 1000 بكسل في الثانية ، ويتحرك بنفس السرعة ويتوقف فجأة بنفس السرعة تمامًا. هذا هو السبب في أن حركة Boxy تبدو آلية وغير طبيعية. سيتعين علينا تغيير الرسم البياني الخاص بنا لإصلاح هذا. لكن قبل التعمق في الأمر ، سنحتاج إلى معرفة كيف ستؤثر التغييرات في السرعة على الرسم البياني المرسوم بين المسافة والوقت. مستعد؟ هذا سيكون ممتعا

دعنا نضاعف سرعة Boxy ونرى كيف يتغير مظهر الرسم البياني استجابةً لذلك. سرعة Boxy الأصلية ، كما حسبنا أعلاه ، هي 1000 بكسل في الثانية. نظرًا لأننا ضاعفنا السرعة ، سيتمكن Boxy الآن من تغطية مسافة 1000 بكسل في نصف الوقت - أي في 0.5 ثانية. دعونا نضع ذلك على الرسم البياني.

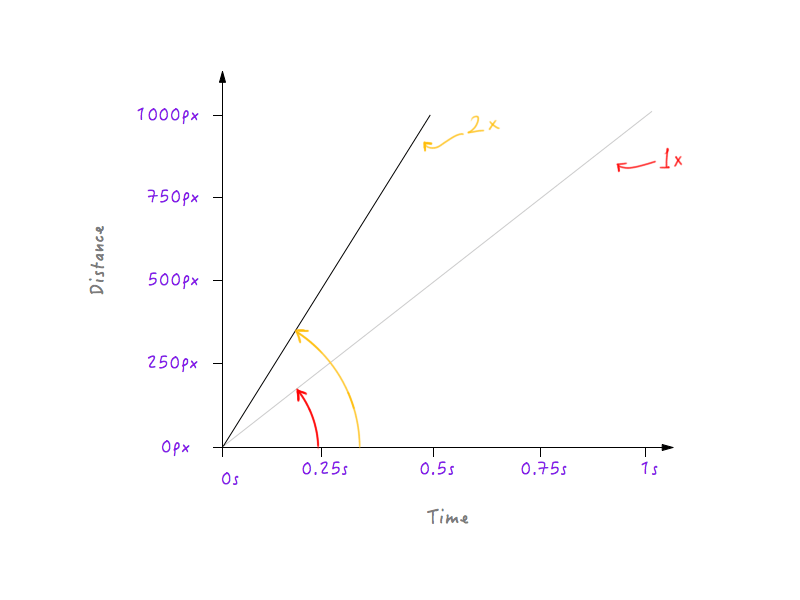
ماذا لو ضاعفنا السرعة ثلاث مرات؟ يغطي Boxy الآن 1000 بكسل في ثلث الوقت (ثلث ثانية).

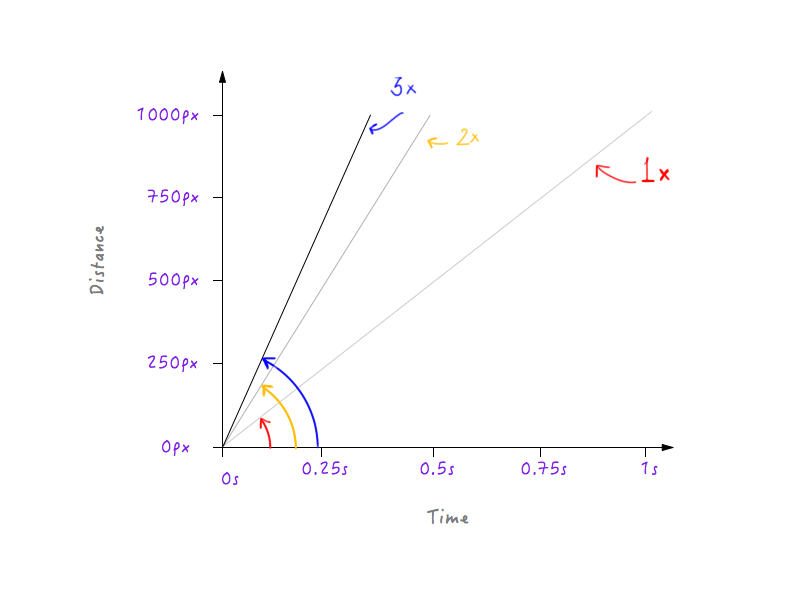
حسنًا ، هل لاحظت شيئًا؟ لاحظ كيف ، عندما يتغير الرسم البياني ، تزداد الزاوية التي يصنعها الخط مع محور الوقت مع زيادة السرعة.

حسنًا ، لنبدأ ونخفض سرعة بوكسي إلى النصف. يعني خفض سرعته إلى النصف أن Boxy سيكون قادرًا على تغطية 500 بكسل فقط (نصف المسافة الأصلية) في ثانية واحدة. دعونا نضع هذا على الرسم البياني.

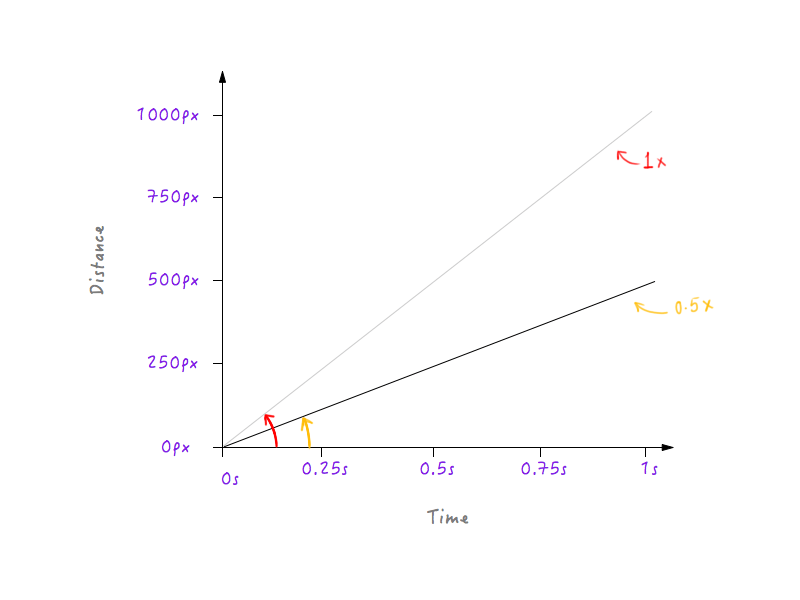
دعنا نبطئ Boxy أكثر قليلاً ، مما يجعل السرعة ثلث السرعة الأصلية. سيتمكن Boxy من تغطية ثلث المسافة الأصلية في ثانية واحدة.

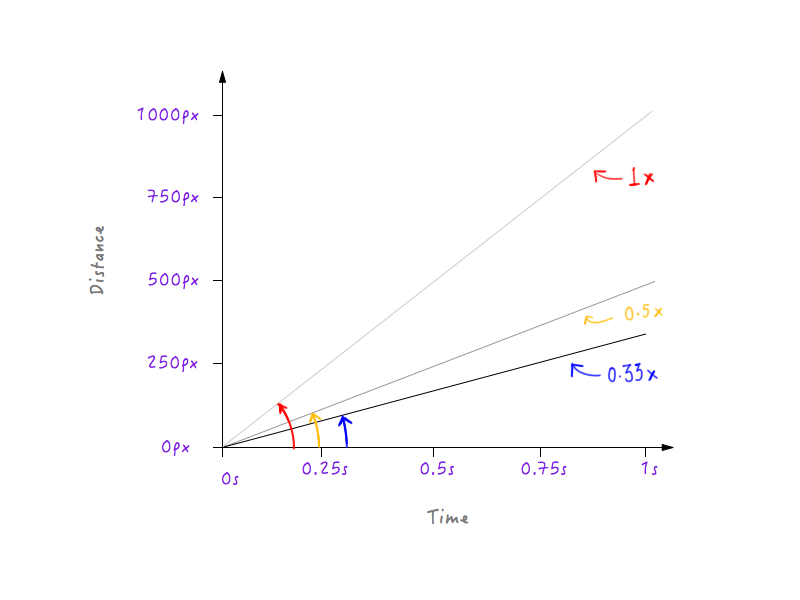
ترى نمط؟ يصبح الخط أكثر انحدارًا وانحدارًا مع زيادة سرعة Boxy ، ويبدأ في التسطيح بينما نبطئ Boxy.

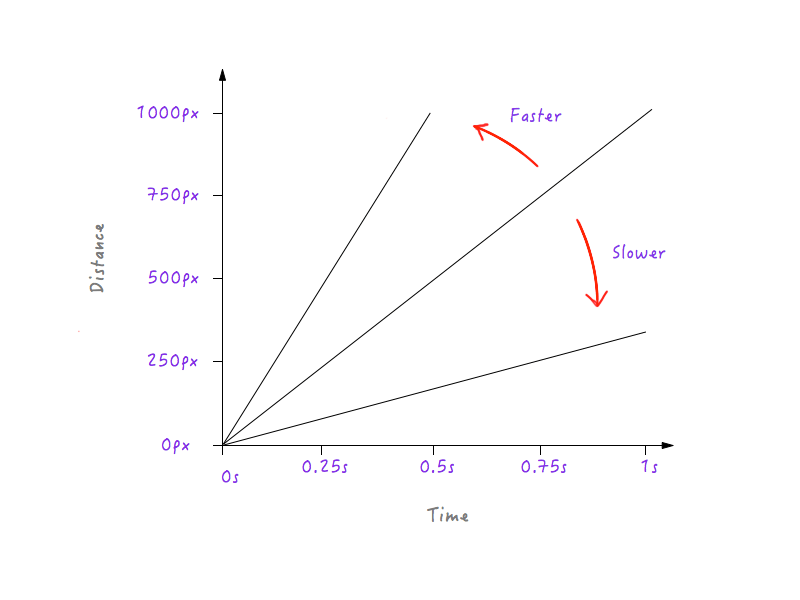
هذا أمر منطقي لأنه ، بالنسبة للخط الأكثر انحدارًا ، ينتج عن تقدم بسيط في الوقت تغيير أعلى بكثير في المسافة ، مما يعني سرعة أكبر.

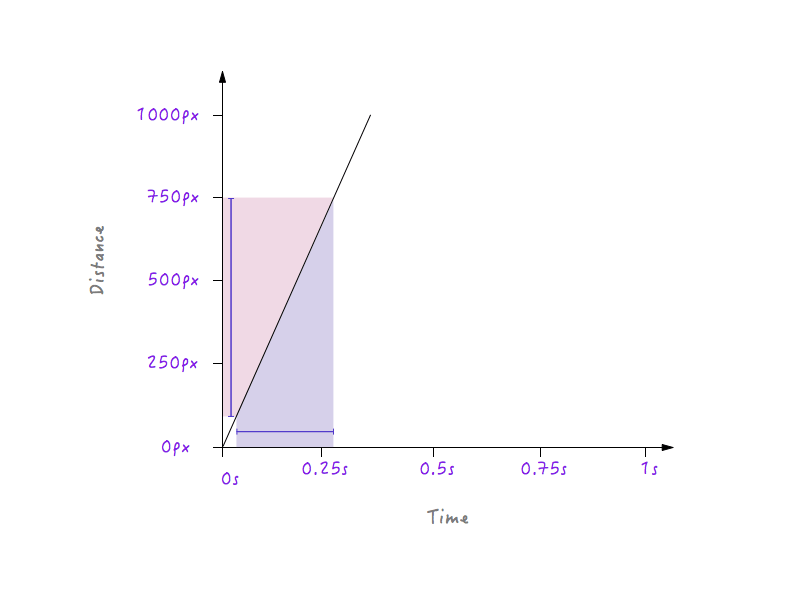
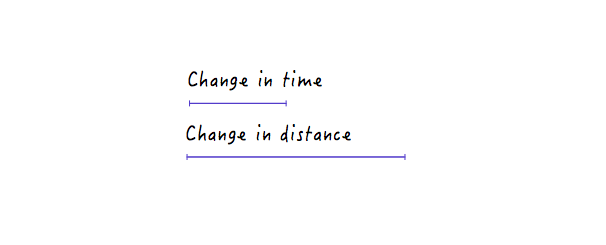
من ناحية أخرى ، بالنسبة للخط الأقل انحدارًا ، ينتج عن التغيير الكبير في الوقت تغييرًا طفيفًا في المسافة ، مما يعني سرعة أقل.

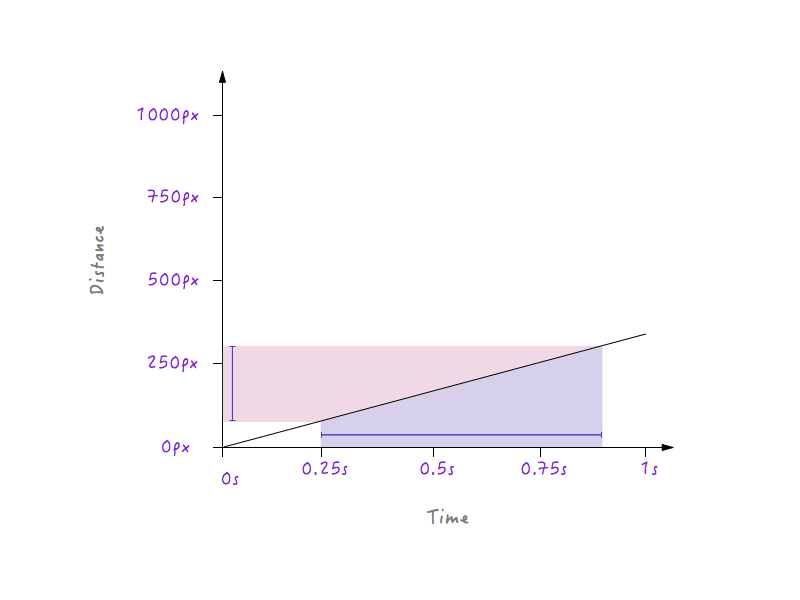
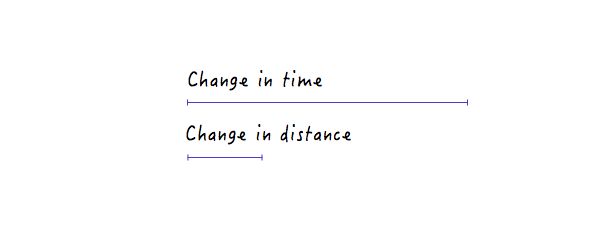
مع كل التغييرات التي أجريناها ، لا يزال Boxy يتحرك بطريقة خطية ، فقط بسرعات مختلفة. ومع ذلك ، مع معرفتنا المكتسبة حديثًا حول كيفية تأثير التغييرات في المسافة مقابل الوقت على السرعة ، يمكننا تجربة ورسم رسم بياني يجعل Boxy يتحرك بطريقة تبدو طبيعية وواقعية.

لنأخذ الأمر خطوة بخطوة. أولاً ، تبدأ الأشياء في الحياة الواقعية ببطء وتزداد سرعتها ببطء. لذا ، لنفعل ذلك.

في جميع تكرارات الرسم البياني الموضحة أدناه ، ستلاحظ أن النقاط الموجودة في الزوايا المقابلة تظل ثابتة. هذا لأننا لا نغير المدة التي تعمل فيها الرسوم المتحركة ، ولا نغير المسافة التي يقطعها Boxy.

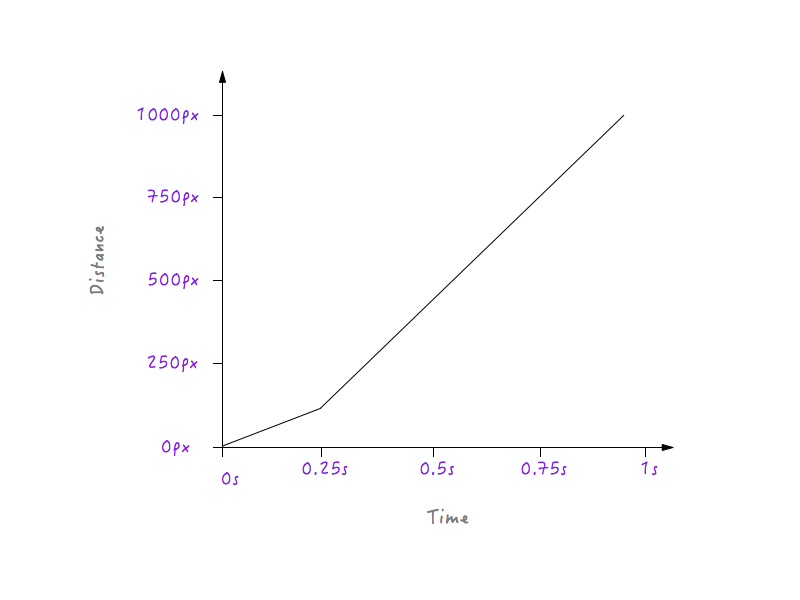
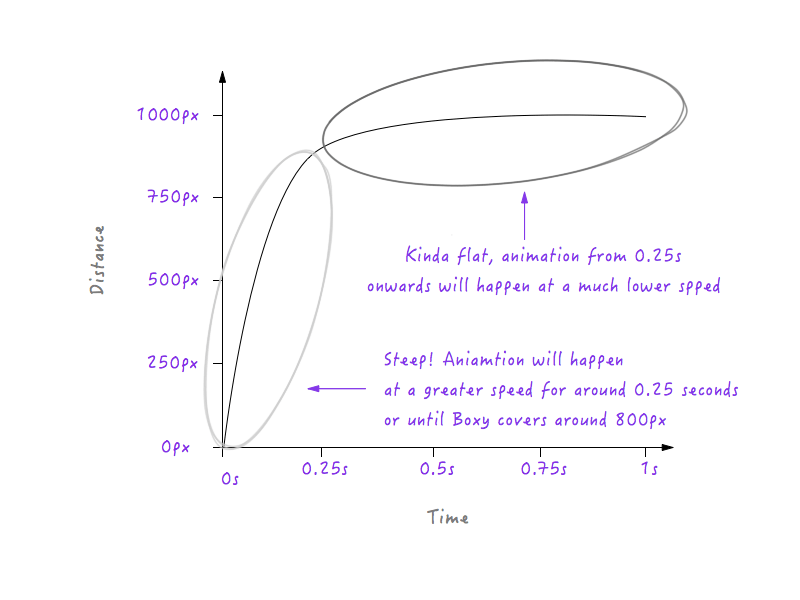
إذا كان Boxy سيتبع الرسم البياني أعلاه ، فسوف يتحرك بسرعة أبطأ لمدة 0.25 ثانية ، لأن الخط أقل انحدارًا بدءًا من 0 إلى 0.25 ثانية ، ثم سيتحول فجأة إلى سرعة أعلى بعد 0.25 ثانية (السبب هو أن الخط في الرسم البياني يصبح أكثر حدة بعد 0.25 ثانية). ومع ذلك ، سنحتاج إلى تسهيل هذا الانتقال ؛ لا نريد أي زوايا - هذا ما يسمى بمنحنى الحركة ، بعد كل شيء. دعونا نحول تلك الزاوية إلى منحنى.

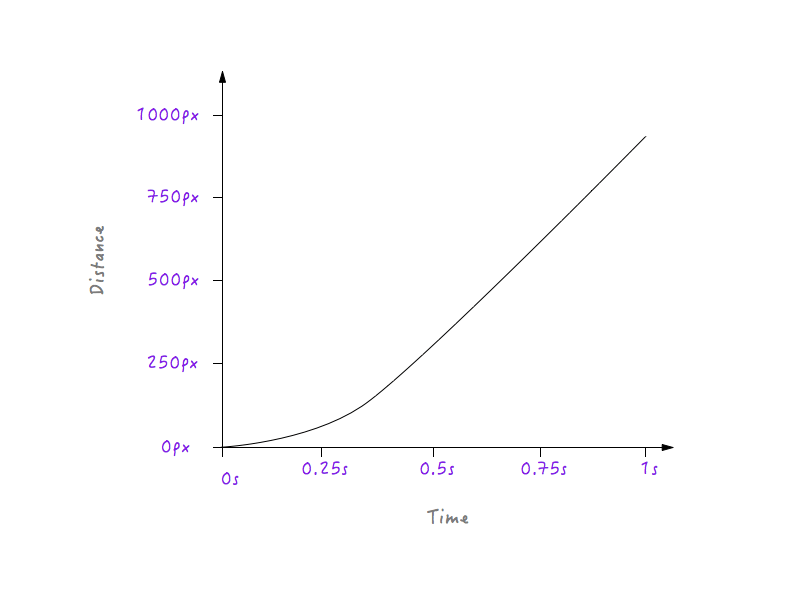
لاحظ الانتقال السلس الذي يمر به Boxy من حالة السكون إلى الزيادة التدريجية في السرعة.

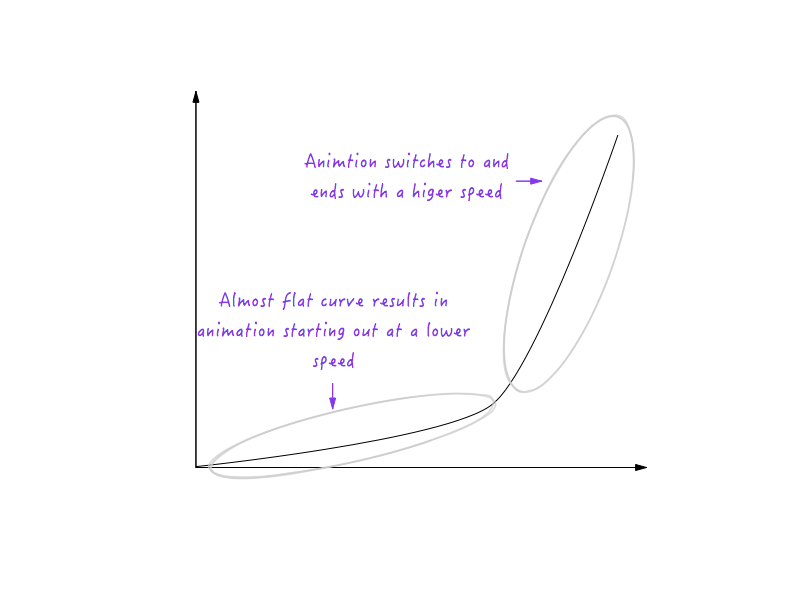
جيد! بعد ذلك ، تتباطأ الأشياء في الحياة الواقعية تدريجياً قبل التوقف. دعنا نغير الرسم البياني لتحقيق ذلك. مرة أخرى ، سنلتقط نقطة زمنية نود بعدها أن يبدأ Boxy في التباطؤ. ماذا عن حوالي 0.6 ثانية؟ لقد سهلت ركن الانتقال إلى منحنى هنا بالفعل.

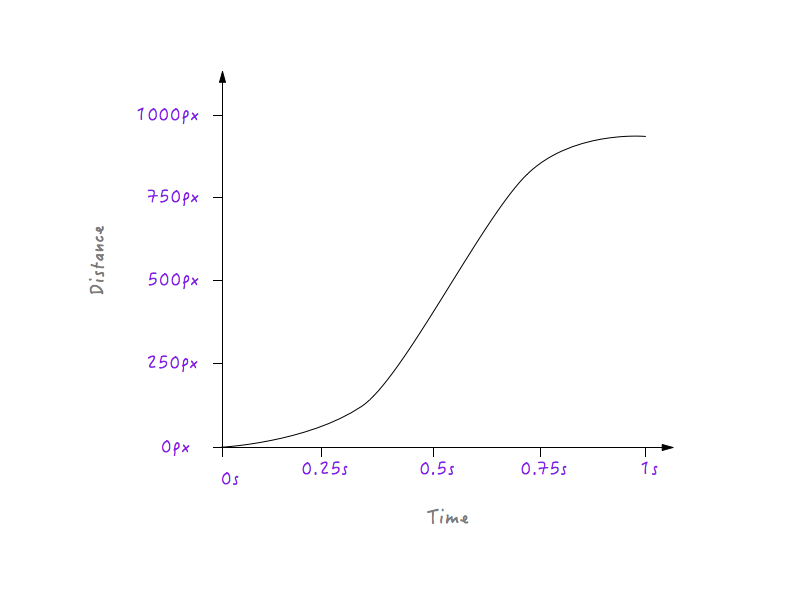
انظر إلى Boxy Go! طبيعي أكثر ، أليس كذلك؟

المنحنى الذي رسمناه في مكان الزاوية هو في الواقع مجموعة من العديد من مقاطع الخطوط الصغيرة ؛ وكما تعلم بالفعل ، كلما كان الخط على الرسم البياني أكثر انحدارًا ، زادت السرعة ، وكلما كان الخط أكثر انبساطًا ، كانت السرعة أبطأ. لاحظ كيف في الجزء الأيسر من الصورة ، تصبح مقاطع الخط التي يتكون منها المنحنى أكثر حدة وانحدارًا ، مما يؤدي إلى زيادة تدريجية في السرعة ، ويتم تسطيحها تدريجياً على الجانب الأيمن ، مما يؤدي إلى تناقص السرعة تدريجيًا؟

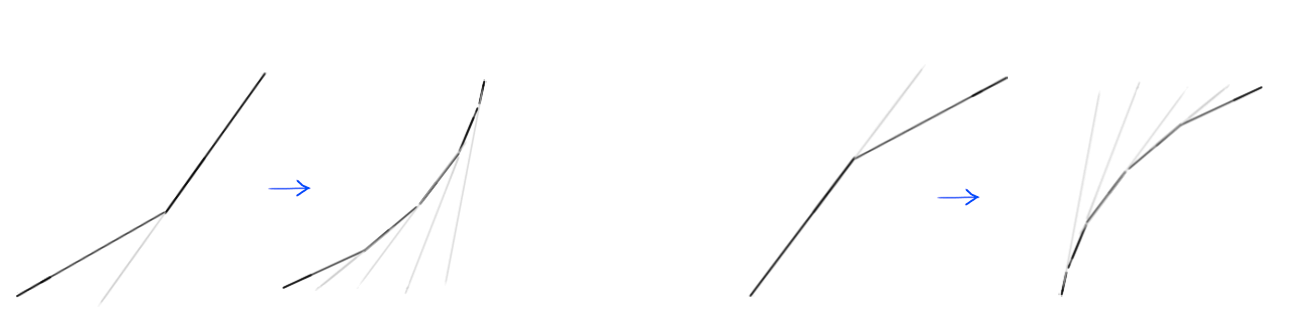
مع كل هذه المعرفة ، يصبح فهم منحنيات الحركة أسهل بكثير. لنلقِ نظرة على بعض الأمثلة.

استخدام منحنيات الحركة في الرسوم المتحركة لواجهة المستخدم

في المرة التالية التي يتعين عليك فيها تحريك عنصر واجهة المستخدم ، سيكون لديك قوة منحنيات الحركة تحت تصرفك. سواء كان شريطًا منزلقًا أو نافذة مشروطة أو قائمة منسدلة ، فإن إضافة المقدار الصحيح من الرسوم المتحركة وجعلها تبدو سلسة وطبيعية ستزيد من جودة واجهة المستخدم الخاصة بك بشكل كبير. سيجعل واجهة المستخدم تشعر بالرضا. خذ القائمة المنسدلة أدناه:

يؤدي النقر فوق قائمة الهامبرغر إلى جلب القائمة من اليسار ، لكن الرسوم المتحركة تبدو ممتلئة. يوضح السطر 51 من CSS أن الرسوم المتحركة بها transition-timing-function مضبوطة على linear . يمكننا تحسين هذا. دعنا ننتقل إلى مكعب بيزير وننشئ وظيفة توقيت مخصصة.

إذا كنت تقرأ هذا ، فمن الآمن أن تفترض أنك مصمم أو مطور أو كليهما ، وبالتالي ، ليس غريبًا على منحنيات البيزير المكعبة ؛ هناك فرصة جيدة لأنك واجهتها مرة واحدة على الأقل. منحنيات بيزير أعجوبة. يتم استخدامها بشكل أساسي في رسومات الكمبيوتر لرسم الأشكال وتستخدم في أدوات مثل Sketch و Adobe Illustrator لرسم رسومات متجهة. السبب وراء شهرة منحنيات البيزير المكعبة هو أنها سهلة الاستخدام: فقط قم بتعديل مواضع النقاط الأربع المختلفة ، وقم بإنشاء نوع المنحنى الذي تحتاجه.

نظرًا لأننا نعرف دائمًا الحالة الأولية والنهائية للكائن المتحرك ، يمكننا إصلاح نقطتين. وهذا يترك نقطتين فقط يتعين علينا تعديل مواقفهما. تسمى النقطتان الثابتتان بنقطتي الربط ، والنقطتان المتبقيتان هما نقطتا تحكم.

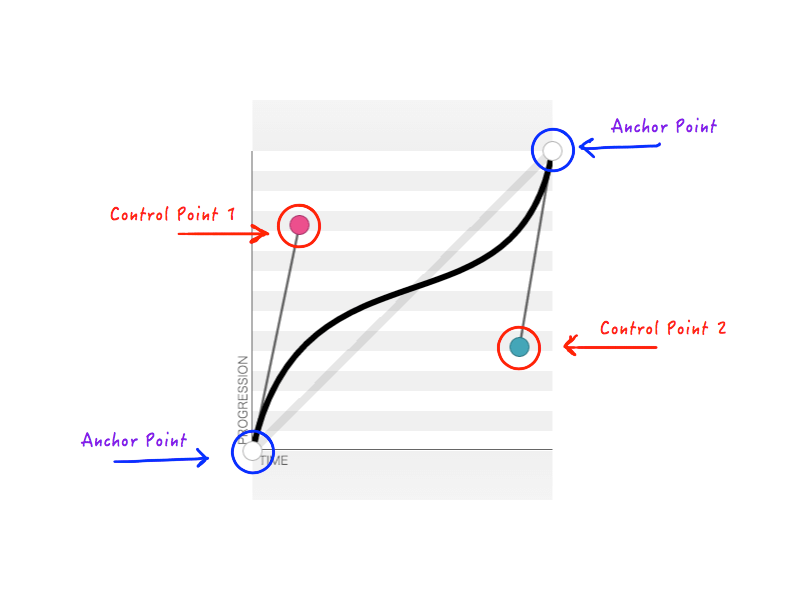
كما تتذكر ، يقبل cubic-bezier أربعة أرقام ( n1, n2, n3, n4 ) عند إنشاء transition-timing-function مخصصة. هذه الأرقام الأربعة لا تمثل شيئًا سوى مواضع نقطتي التحكم: n1, n2 تمثل إحداثيات x و y لنقطة التحكم الأولى ، و n3, n4 تمثل إحداثيات نقطة التحكم الثانية. نظرًا لأن تغيير موضع نقاط التحكم سيغير شكل المنحنى ، وبالتالي ، الرسوم المتحركة لدينا بشكل عام ، فإن النتيجة هي نفسها عند تعديل أي من أو كل n1, n2, n3, n4 . على سبيل المثال ، يمثل الشكل أدناه cubic-bezier(.14, .78, .89, .35) :

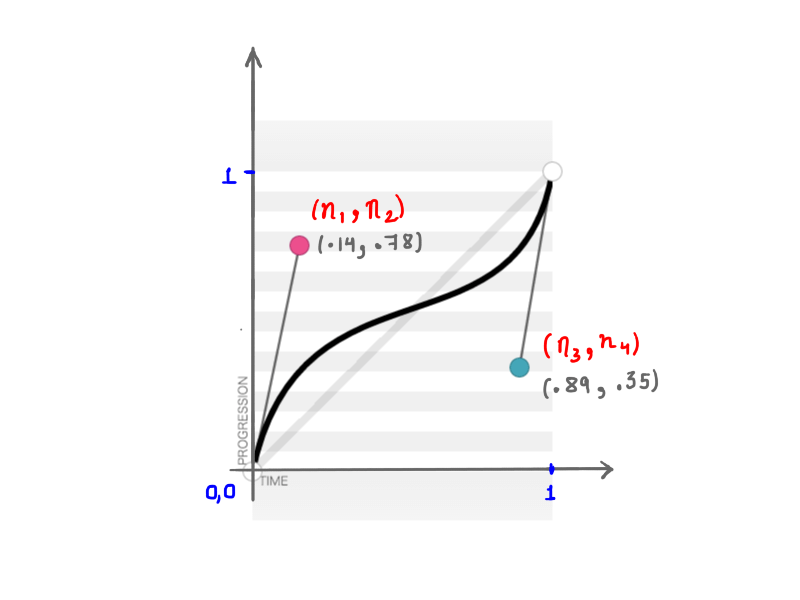
الرياضيات وراء هذه المنحنيات التي تبدو بسيطة رائعة.

حسنًا ، حسنًا ، دعنا نعود إلى حيث كنا ذاهبون مع مكعب بيزير: إنشاء وظيفة transition-timing-function مخصصة. أريد نوع الرسوم المتحركة الذي تنزلق فيه القائمة بسرعة كبيرة ثم تتباطأ وتنتهي برشاقة:

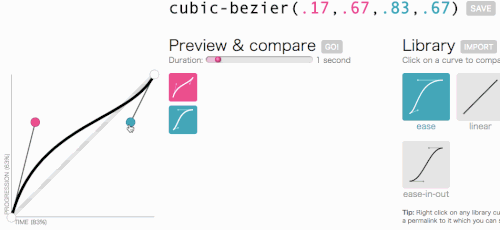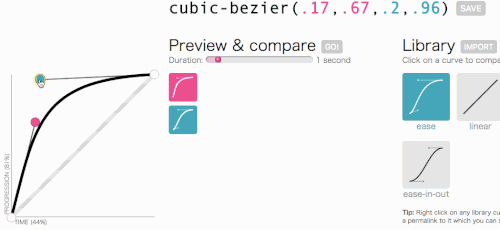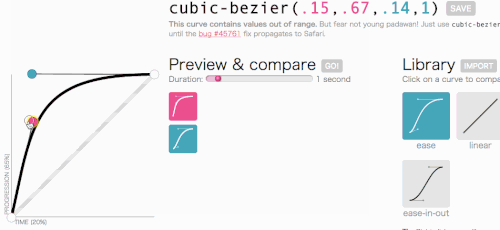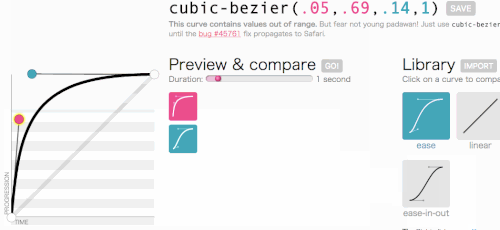
هذا يبدو جيدا. ستبدأ الرسوم المتحركة بسرعة ثم تبطئ ، بدلاً من التحرك بسرعة ثابتة طوال الوقت. سأقوم ببساطة بنسخ cubic-bezier(.05, .69, .14, 1) من أعلى الصفحة واستبدال linear به.

ترى الفرق؟ يبدو التكرار الثاني أكثر طبيعية وجاذبية. تخيل لو أن كل الرسوم المتحركة في واجهة المستخدم الخاصة بك تتبع وظيفة توقيت طبيعية. كم من الرائع أن يكون ذلك؟

كما رأينا ، منحنيات الحركة ليست صعبة على الإطلاق. إنها سهلة الفهم والاستخدام. معهم ، يمكنك نقل واجهة المستخدم الخاصة بك إلى المستوى التالي.

أتمنى أن تكون قد تعلمت كيف تعمل منحنيات الحركة. إذا كنت تمر بالكثير من التجارب والخطأ لجعل منحنيات الحركة تعمل بالطريقة التي تريدها ، أو إذا لم تكن تستخدمها على الإطلاق ، فيجب أن تشعر بالراحة الآن في ثنيها حسب إرادتك وإنشاء رسوم متحركة جميلة. لأنه ، بعد كل شيء ، الرسوم المتحركة مهمة.