مشتق من قواعد السلسلة في التعلم الآلي: شرح

لقد تطور التعلم الآلي ليصبح أحد أكثر المجالات التي تم الحديث عنها والبحث عنها في السنوات الحالية ، ولجميع الأسباب الوجيهة. يتم اكتشاف نماذج وتطبيقات جديدة للتعلم الآلي كل يوم ، ويعمل الباحثون في جميع أنحاء العالم على تحقيق الشيء الكبير التالي.

نتيجة لذلك ، كان هناك اهتمام متزايد بالمحترفين من خلفيات متنوعة للتبديل إلى التعلم الآلي والمشاركة في هذه الثورة المستمرة. إذا كنت أحد هؤلاء المتحمسين للتعلم الآلي الذي يتطلع إلى اتخاذ خطواتهم الأولى ، فلنخبرك أنه يبدأ بفهم أساسيات الرياضيات والإحصاء قبل أي شيء آخر.

المشتقات هي أحد الموضوعات الحيوية في الرياضيات والتي لها صلة وثيقة بالتعلم الآلي. من فهمك الأساسي لحساب التفاضل والتكامل ، ستتذكر أن مشتق أي دالة هو معدل التغير اللحظي لتلك الدالة. في هذه المدونة ، سنتعمق في المشتقات ونستكشف قاعدة السلسلة. سنرى كيف يتغير ناتج وظيفة معينة عندما نغير بعض المتغيرات المستقلة في المعادلة. من خلال معرفة مشتقات قواعد السلسلة ، ستتمكن من العمل على تمييز الوظائف الأكثر تعقيدًا التي من المؤكد أنك ستواجهها في التعلم الآلي.

احصل على شهادة التعلم الآلي عبر الإنترنت من أفضل الجامعات في العالم - الماجستير ، وبرامج الدراسات العليا التنفيذية ، وبرنامج الشهادة المتقدم في ML & AI لتسريع حياتك المهنية.

فهم مشتق قاعدة السلسلة

قاعدة السلسلة هي أساسًا صيغة رياضية تساعدك في حساب مشتق دالة مركبة. الوظيفة المركبة هي الوظيفة التي تتكون من وظيفتين أو أكثر. لذا ، إذا كانت f و g وظيفتين ، فإن قاعدة السلسلة ستساعدنا في إيجاد مشتقة الدوال المركبة مثل fog أو go f.

بالنظر إلى ضباب الوظيفة المركبة ، إليك ما سيبدو عليه مشتق قاعدة السلسلة:

يمكن أيضًا كتابة القاعدة المذكورة أعلاه على النحو التالي:

حيث تكون الوظيفة F هي تكوين f و g في شكل f (g (x)).

الآن ، لنفترض أن لدينا ثلاثة متغيرات مثل أن المتغير الثالث (z) يعتمد على المتغير الثاني (y) ، والذي بدوره يعتمد على المتغير الأول (x). في هذه الحالة ، سيبدو مشتق قاعدة السلسلة كما يلي:

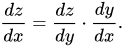فيما يتعلق بالتعلم العميق ، هذه أيضًا الصيغة المستخدمة بانتظام لحل مشاكل التكاثر العكسي. بما أننا ذكرنا أن z يعتمد على y و y على x ، فيمكننا كتابة z = f (y) و y = g (x). سيؤدي هذا الاستبدال إلى تعديل معادلتنا التفاضلية بالطريقة التالية:

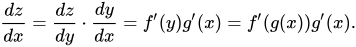الآن ، دعنا نلقي نظرة على بعض أمثلة مشتقات قواعد السلسلة لفهم الرياضيات التي وراءها بشكل أفضل.

أمثلة وتطبيقات مشتق قواعد السلسلة

لنأخذ مثالًا مشهورًا من ويكيبيديا لفهم مشتق قاعدة السلسلة بطريقة أفضل. افترض أنك تسقط من السماء. الضغط الجوي الذي تواجهه خلال الخريف سوف يتغير باستمرار. فيما يلي رسم بياني يوضح هذا التغيير في الضغط الجوي مع مستويات الارتفاع:

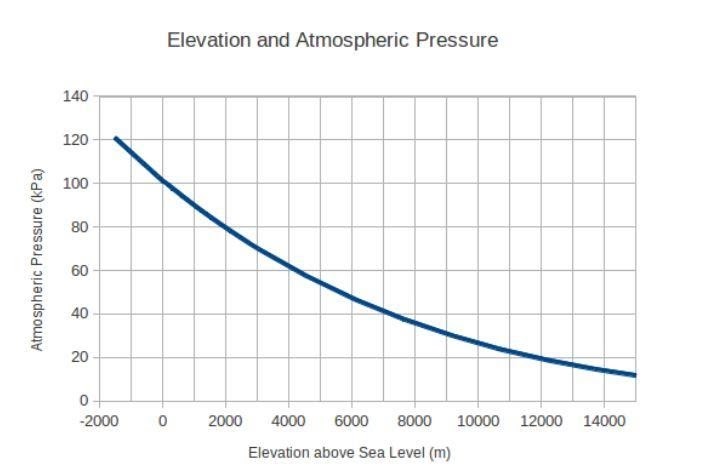
لنفترض أن سقوطك بدأ على ارتفاع 4000 متر فوق مستوى سطح البحر. في البداية ، كانت سرعتك صفرًا ، وكانت قيمة العجلة 9.8 مترًا لكل ثانية مربعة بسبب الجاذبية.

الآن ، لنقارن هذا الموقف مع طريقة قاعدة السلسلة السابقة. في هذا المثال ، سنستخدم المتغير "t" للوقت بدلاً من x.

بعد ذلك ، يمكن إعطاء المتغير y = g (t) ، الذي يخبرنا بالمسافة المقطوعة منذ بداية السقوط ، على النحو التالي:

ز (ر) = 0.5 * 9.8 طن ^ 2

ويمكن تحديد الارتفاع من مستوى سطح البحر بواسطة المتغير "h" ، والذي سيساوي 400-g (t).

افترض أنه بناءً على نموذج ما ، يمكننا أيضًا كتابة دالة الضغط الجوي عند أي ارتفاع h على النحو التالي:

و (ح) = 101325 هـ − 0.0001 س

الآن ، يمكنك التمييز بين المعادلتين بناءً على المتغيرات التابعة لهما للحصول على النتائج التالية:

ز ′ (ر) = −9.8 طن ،

هنا ، g '(t) تخبرنا بقيمة سرعتك في أي وقت t.

و ′ (ح) = −10.1325e − 0.0001 س

هنا f ′ (h) هو معدل التغير في الضغط الجوي بالنسبة للارتفاع h. الآن ، السؤال هو هل يمكننا دمج هاتين المعادلتين واشتقاق معدل تغير ضغط أجهزة الصراف الآلي بالوقت؟ دعونا نرى استخدام قاعدة السلسلة:

تقدم لنا المعادلة الأخيرة التي حصلنا عليها معدل تغير الضغط الجوي بالنسبة إلى الوقت المنقضي منذ السقوط. فيما يتعلق بالتعلم الآلي ، تحتاج الشبكات العصبية باستمرار إلى تحديثات الوزن المتعلقة بخطأ الخلايا العصبية في التنبؤ. تساعد قاعدة السلسلة في ضبط هذه الأوزان وتقريب نموذج التعلم الآلي من الناتج الصحيح.

خاتمة

كما ترى ، فإن قاعدة السلسلة مفيدة للعديد من الأغراض. خاصة عندما يتعلق الأمر بالتعلم الآلي أو التعلم العميق ، تجد قاعدة السلسلة فائدة كبيرة في تحديث أوزان الخلايا العصبية وتحسين الكفاءة الكلية للنموذج.

الآن بعد أن أصبحت على دراية بأساسيات قاعدة السلسلة ، جرب بعض المشكلات بنفسك. ابحث عن بعض الدوال المركبة وحاول إيجاد مشتقاتها. كلما تدربت أكثر ، أصبحت مفاهيمك أكثر وضوحًا ، وسيكون من الأسهل عليك تدريب نماذج التعلم الآلي الخاصة بك! ومع ذلك ، إذا كنت من عشاق التعلم الآلي ولكنك تكافح من أجل اتخاذ خطواتك الأولى في هذا المجال ، فإن upGrad تدعمك!

يتم تقديم برنامج PG التنفيذي في التعلم الآلي والذكاء الاصطناعي بالتعاون مع IIIT -Bangalore ويمنحك الاختيار من بين ستة تخصصات ذات صلة بالصناعة. تبدأ الدورة من المستوى الأرضي وتنقلك إلى القمة مع تزويدك بالدعم الفردي من خبراء الصناعة ومجموعة أقران قوية من الطلاب ودعم مهني 360 درجة.