إحصائيات ونموذج بايزي: شرح

تقنية بايز هي طريقة في الإحصاء تستخدم في تحليل البيانات وتقدير المعلمات. يعتمد هذا النهج على نظرية بايز.

تتبع Bayesian Statistics مبدأً فريدًا حيث تساعد في تحديد التوزيع الاحتمالي المشترك للمعلمات المرصودة وغير المرصودة باستخدام نموذج إحصائي. المعرفة الإحصائية ضرورية لمعالجة المشاكل التحليلية في هذا السيناريو.

منذ أن قدم توماس بايز نظرية بايز في سبعينيات القرن الثامن عشر ، ظلت أداة لا غنى عنها في الإحصاء. تعد نماذج بايز بديلاً كلاسيكيًا للنماذج المتكررة حيث ساعدت الابتكارات الحديثة في الإحصاء في اختراق المعالم في مجموعة واسعة من الصناعات ، بما في ذلك البحث الطبي وفهم عمليات البحث على الويب ومعالجة اللغات الطبيعية (معالجة اللغة الطبيعية).

على سبيل المثال ، مرض الزهايمر هو مرض معروف بأنه يشكل خطرًا متزايدًا مع تقدم العمر. ومع ذلك ، بمساعدة نظرية بايز ، يمكن للأطباء تقدير احتمالية إصابة الشخص بمرض الزهايمر في المستقبل. وينطبق أيضًا على السرطان والأمراض الأخرى المرتبطة بالعمر التي يصبح الشخص عرضة لها في السنوات الأخيرة من حياته.

إحصائيات متكررة مقابل إحصائيات بايزي

لطالما كانت الإحصائيات المتكررة مقابل إحصائيات بايز موضوعًا للجدل والكوابيس للمبتدئين ، وكلاهما يواجه صعوبة في الاختيار بين الاثنين. في أوائل القرن العشرين ، خضعت إحصاءات بايز لنصيبها من قضايا عدم الثقة والقبول. ومع مرور الوقت ، أدرك الناس إمكانية تطبيق نماذج بايز والحلول الدقيقة التي تنتج عنها.

فيما يلي نلقي نظرة على الإحصائيات المتكررة والتعقيدات المرتبطة بها:

إحصائيات متكررة

إنها منهجية استنتاجية مستخدمة على نطاق واسع في عالم الإحصاء. يحلل ما إذا كان حدث ما (مذكور كفرضية) قد وقع أم لا. كما أنها تقدر احتمالية وقوع الحدث خلال فترة التجربة. تتكرر التجربة حتى تتحقق النتيجة المرجوة.

عينات التوزيع الخاصة بهم ذات حجم حقيقي ، والتجربة تتكرر مرات لا نهائية من الناحية النظرية. فيما يلي مثال يوضح كيف يمكن استخدام الإحصائيات المتكررة لدراسة رمي عملة معدنية.

• إمكانية الحصول على رأس عند رمي العملة مرة واحدة هي 0.5 (1/2).
• يشير عدد الرؤوس إلى العدد الفعلي للعملاء المتوقعين.
• سيزداد الفرق بين العدد الفعلي للرؤوس والعدد المتوقع للرؤوس مع زيادة عدد الرميات.

إذن هنا ، تعتمد النتيجة على عدد مرات تكرار التجربة. إنه عيب رئيسي للإحصاءات المتكررة.

أصبحت العيوب الأخرى المرتبطة بتقنيات التصميم والتفسير واضحة في القرن العشرين عندما كان تطبيق الإحصائيات المتكررة على النماذج العددية في ذروته.

حدود الإحصائيات المتكررة

يتم سرد العيوب الثلاثة الرئيسية للإحصاءات المتكررة أدناه:

1. متغير ف القيم

تم قياس قيم p لعينة ذات حجم ثابت في تجربة مع تغيير نقطة نهاية محددة مع أي تغيير في نقطة النهاية وحجم العينة. ينتج عنه قيمتان p لبيانات واحدة وهي غير صحيحة.

2. فترات الثقة غير متسقة

CI (فترة الثقة) تعتمد فقط على حجم العينة. يجعل إمكانية التوقف غير ذات صلة.

3. القيم المقدرة ل CI

فترات الثقة ليست توزيعًا احتماليًا ، وقيمها للمعامل ما هي إلا تقدير وليست قيمًا فعلية.

أدت الأسباب الثلاثة المذكورة أعلاه إلى ولادة نهج بايزي الذي يطبق الاحتمالات على المشكلات الإحصائية.

ولادة إحصائيات بايزي

اقترح القس توماس بايز لأول مرة نهج بايزي للإحصاء في مقالته المكتوبة عام 1763. وقد نشر ريتشارد برايس هذا النهج كاستراتيجية في الاحتمال العكسي للتنبؤ بالأحداث المستقبلية بناءً على الماضي.

يعتمد النهج على نظرية بايز الموضحة أدناه:

مبرهنة بايز

تدرس بديهية Renyi للاحتمالات الاحتمالات الشرطية ، حيث تكون احتمالات وقوع الحدث A والحدث B تابعة أو مشروطة. يمكن كتابة الاحتمال الشرطي الأساسي على النحو التالي:

يعتمد احتمال وقوع الحدث "ب" على الحدث "أ".

المعادلة أعلاه هي أساس قاعدة بايز ، وهي تعبير رياضي لنظرية بايز التي تنص على:

هنا ، تشير إلى التقاطع.

يمكن كتابة قاعدة بايز على النحو التالي:

قاعدة Bayes هي أساس إحصائيات Bayesian ، حيث تتم مقارنة المعلومات المتاحة حول معلمة معينة في نموذج إحصائي وتحديثها بالبيانات التي تم جمعها.

يتم تمثيل المعرفة الأساسية على أنها التوزيع السابق ، والذي تتم مقارنته بعد ذلك ودراسته مع البيانات المرصودة أو المجمعة كدالة احتمالية لمعرفة التوزيع اللاحق.

يستخدم هذا التوزيع اللاحق لعمل تنبؤات حول الأحداث المستقبلية.

تعتمد تطبيقات نهج بايزي على المعلمات التالية:

1. تحديد النموذج السابق والبيانات
2. صنع الاستدلالات ذات الصلة
3. التدقيق في النماذج وتبسيطها

ما هي شبكات بايزي العصبية؟

شبكات Bayesian Neural Networks (BNNs) هي شبكات تقوم بإنشائها عندما تقوم بتوسيع الشبكات القياسية باستخدام المنهجية الإحصائية وتغيير الاستدلال اللاحق لتتبع الإفراط في الملاءمة. نظرًا لأنه نهج بايزي ، فهناك توزيع احتمالي مرتبط بمعلمات الشبكات العصبية.

يتم استخدامها لحل المشكلات المعقدة حيث لا يتوفر التدفق الحر للبيانات. تساعد الشبكات العصبية البايزية في التحكم في التخصيص الزائد في مجالات مثل البيولوجيا الجزيئية والتشخيص الطبي.

يمكن للمرء أن يفكر في توزيع كامل للإجابات على سؤال بدلاً من مجرد احتمال واحد باستخدام شبكات Bayesian العصبية. أنها تساعدك على تحديد اختيار / مقارنة النموذج ومعالجة المشاكل التي تنطوي على تسوية.

تقدم إحصائيات بايز أدوات رياضية لترشيد وتحديث المعرفة الذاتية المتعلقة بالبيانات الجديدة أو الأدلة العلمية. على عكس النهج الإحصائي المتكرر ، فإنه يعمل على أساس افتراض أن الاحتمالات تعتمد على تكرار الأحداث المتكررة في ظل نفس الظروف.

باختصار ، تقنية بايز هي امتداد لافتراض الفرد وآرائه. الجانب الرئيسي لنموذج بايزي الذي يجعله أكثر كفاءة هو فهمه أن الأفراد يختلفون في آرائهم بناءً على نوع المعلومات التي يتلقونها.

ومع ذلك ، مع ظهور أدلة وبيانات جديدة ، يكون لدى الأفراد نقطة تقارب ، وهي الاستدلال البايزي . هذا التحديث العقلاني هو السمة الخاصة لإحصاءات بايز التي تجعلها أكثر فاعلية في المشكلات التحليلية.

هنا ، يتم تطبيق احتمال 0 عندما لا يكون هناك أمل لوقوع حدث ، ويتم تطبيق احتمال 1 عندما يتم التأكد من حدوث الحدث. يعطي الاحتمال بين 0 و 1 مساحة للنتائج المحتملة الأخرى.

يتم تطبيق قاعدة بايز الآن لتحقيق الاستدلال البايزي للحصول على استنتاج أفضل من النموذج.

كيف تطبق قاعدة بايز للحصول على الاستدلال بايزي؟

ضع في اعتبارك المعادلة:

الفوسفور (θ | د) = الفوسفور (د | θ.) الفوسفور (θ) / الفوسفور (د)

تشير P (θ) إلى التوزيع السابق ،

تشير P (θ | D) إلى الإيمان اللاحق ،

تمثل P (D) الدليل ،

تشير P (D | θ) إلى الاحتمالية.

الهدف الرئيسي من الاستدلال البايزي هو تقديم طريقة عقلانية ودقيقة من الناحية الحسابية لدمج المعتقدات مع الأدلة للحصول على معتقدات لاحقة محدثة. يمكن استخدام المعتقدات اللاحقة كمعتقدات سابقة عند إنشاء بيانات جديدة. وبالتالي ، يساعد الاستدلال البايزي على تحديث المعتقدات باستمرار بمساعدة قاعدة بايز.

بالنظر إلى نفس مثال تقليب العملة ، يقوم نموذج Bayesian بتحديث الإجراء من قبل إلى المعتقدات اللاحقة مع تقليب العملة الجديدة. تعطي طريقة بايز الاحتمالات التالية.

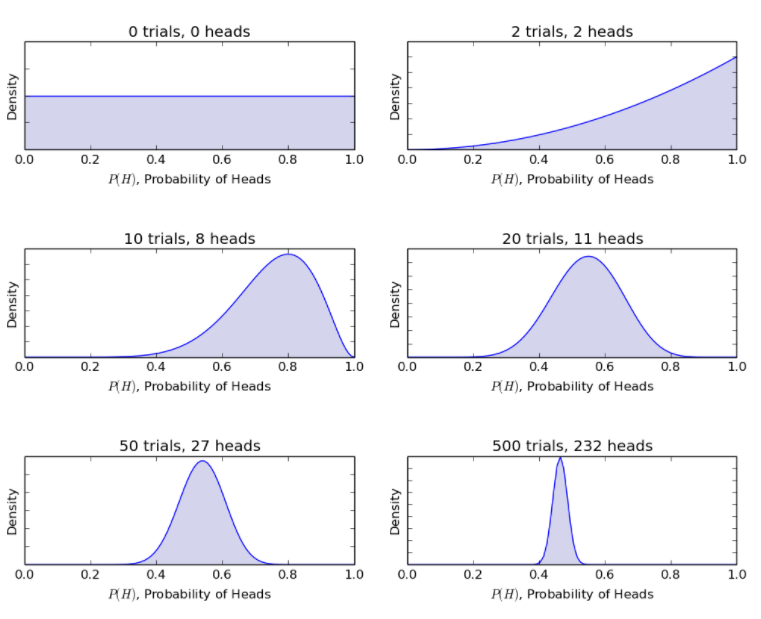
مصدر

وبالتالي ، يسمح نموذج بايز بترشيد سيناريو غير مؤكد بمعلومات مقيدة إلى سيناريو أكثر تحديدًا مع قدر كبير من البيانات.

اختلافات ملحوظة بين نموذج بايزي والنموذج المتكرر

إحصائيات متكررة

إحصائيات بايزي

يعتبر الهدف بمثابة تقدير نقطي ، و CI

يعتبر الهدف التوزيع اللاحق

يبدأ الإجراء من الملاحظات

تبدأ العملية من التوزيع السابق

كلما تم إجراء ملاحظات جديدة ، فإن النهج التكراري يعيد حساب النموذج الحالي.

كلما تم إجراء ملاحظات جديدة ، يتم تحديث التوزيع اللاحق (الأيديولوجيا / الفرضية)

أمثلة: تقدير المتوسط ​​واختبار t و ANOVA.

أمثلة: تقدير التوزيع اللاحق لمتوسط ​​وتداخل فترات الكثافة العالية.

مزايا الإحصاء البايزي

• يوفر وسيلة عضوية وبسيطة لدمج المعلومات المسبقة مع إطار عمل قوي مع الأدلة العلمية. يمكن استخدام المعلومات السابقة حول المعلمة لتشكيل توزيع مسبق للتحقيق في المستقبل. تلتزم الاستنتاجات بنظرية بايز.
• الاستنتاجات من نموذج بايز منطقية ودقيقة رياضيا وليست افتراضات خام. تظل الدقة ثابتة بغض النظر عن حجم العينة.
• تتبع إحصائيات بايزي مبدأ الاحتمالية. عندما يكون لعينتين مختلفتين دالة احتمالية مشتركة لاعتقاد ، يجب أن تكون جميع الاستنتاجات حول الاعتقاد متشابهة. لا تتبع الأساليب الإحصائية الكلاسيكية مبدأ الاحتمالية.
• يمكن تفسير الحلول من تحليل بايزي بسهولة.
• إنه يوفر منصة مواتية لنماذج مختلفة مثل النماذج الهرمية وقضايا البيانات غير المكتملة. يمكن تتبع حسابات جميع النماذج البارامترية تقريبًا بمساعدة تقنيات عددية أخرى.

التطبيقات الناجحة لنماذج بايز عبر التاريخ

كان لأساليب بايز الكثير من التطبيقات الناجحة خلال الحرب العالمية الثانية. وترد أدناه بعض منها:

• نجح الإحصائي الروسي أندريه كولموغوروف في استخدام أساليب بايز لتحسين كفاءة المدفعية الروسية.
• تم استخدام نماذج بايزي لكسر رموز قوارب U الألمانية.
• ساعد عالم الرياضيات الأمريكي المولود في فرنسا ، برنارد كوبمان ، الحلفاء في تحديد موقع قوارب U الألمانية بمساعدة نماذج بايز لاعتراض الإرسال اللاسلكي.

إذا كنت ترغب في معرفة المزيد عن إحصائيات بايز ، فإليك شهادة جراد المتقدمة في التعلم الآلي والسحابة لفهم المفاهيم الأساسية من خلال مشاريع الصناعة الواقعية ودراسات الحالة. يتم تقديم الدورة التي تبلغ مدتها 12 شهرًا بواسطة IIT Madras وتدعم التعلم الذاتي.

تواصل معنا لمزيد من التفاصيل.