نظرية بايز في التعلم الآلي: مقدمة ، كيفية التطبيق ومثال
نشرت: 2021-02-04جدول المحتويات
مقدمة: ما هي نظرية بايز؟
تم تسمية نظرية بايز على اسم عالم الرياضيات الإنجليزي توماس بايز ، الذي عمل على نطاق واسع في نظرية القرار ، مجال الرياضيات الذي يتضمن الاحتمالات. تُستخدم نظرية بايز أيضًا على نطاق واسع في التعلم الآلي ، حيث إنها طريقة بسيطة وفعالة للتنبؤ بالفصول الدراسية بدقة ودقة. تُستخدم طريقة بايز لحساب الاحتمالات الشرطية في تطبيقات التعلم الآلي التي تتضمن مهام التصنيف.
يتم استخدام نسخة مبسطة من نظرية بايز ، والمعروفة باسم تصنيف بايز السذاجة ، لتقليل وقت الحساب والتكاليف. في هذه المقالة ، نأخذك عبر هذه المفاهيم ونناقش تطبيقات نظرية بايز في التعلم الآلي.
انضم إلى دورة التعلم الآلي عبر الإنترنت من أفضل الجامعات في العالم - الماجستير ، وبرامج الدراسات العليا التنفيذية ، وبرنامج الشهادات المتقدمة في ML & AI لتسريع حياتك المهنية.
لماذا نستخدم نظرية بايز في التعلم الآلي؟
نظرية بايز هي طريقة لتحديد الاحتمالات الشرطية - أي احتمالية وقوع حدث ما بالنظر إلى وقوع حدث آخر بالفعل. نظرًا لأن الاحتمال الشرطي يتضمن شروطًا إضافية - بمعنى آخر ، المزيد من البيانات - يمكن أن يساهم في نتائج أكثر دقة.
وبالتالي ، فإن الاحتمالات الشرطية ضرورية في تحديد التنبؤات والاحتمالات الدقيقة في التعلم الآلي. بالنظر إلى أن المجال أصبح أكثر انتشارًا في كل مكان عبر مجموعة متنوعة من المجالات ، فمن المهم فهم دور الخوارزميات والطرق مثل نظرية بايز في التعلم الآلي.
قبل أن ندخل في النظرية نفسها ، دعونا نفهم بعض المصطلحات من خلال مثال. لنفترض أن مدير مكتبة لديه معلومات حول عمر عملائه ودخلهم. يريد أن يعرف كيف يتم توزيع مبيعات الكتب على ثلاث فئات عمرية للعملاء: الشباب (18-35) ، منتصف العمر (35-60) ، وكبار السن (60+).

دعونا نطلق على بياناتنا اسم X. في مصطلحات بايزي ، يُطلق على X دليل. لدينا بعض الفرضيات H ، حيث لدينا بعض X ينتمي إلى فئة معينة C.
هدفنا هو تحديد الاحتمال الشرطي لفرضيتنا H معطى X ، أي P (H | X).
بعبارات بسيطة ، من خلال تحديد P (H | X) ، نحصل على احتمال انتماء X إلى الفئة C ، نظرًا لأن X لها سمات العمر والدخل - دعنا نقول ، على سبيل المثال ، 26 عامًا بدخل 2000 دولار. H هي فرضيتنا أن العميل سيشتري الكتاب.
انتبه جيدًا للمصطلحات الأربعة التالية:
- الدليل - كما تمت مناقشته سابقًا ، يُعرف P (X) بالدليل. إنه ببساطة احتمال أن يكون العميل ، في هذه الحالة ، يبلغ من العمر 26 عامًا ، ويحصل على 2000 دولار.
- الاحتمال المسبق - P (H) ، المعروف باسم الاحتمال السابق ، هو الاحتمال البسيط لفرضيتنا - أي أن العميل سيشتري كتابًا. لن يتم تزويد هذا الاحتمال بأي مدخلات إضافية بناءً على العمر والدخل. نظرًا لأن الحساب يتم باستخدام معلومات أقل ، فإن النتيجة تكون أقل دقة.
- يُعرف الاحتمال الخلفي - P (H | X) بالاحتمال اللاحق. هنا ، P (H | X) هو احتمال أن يشتري العميل كتابًا (H) إذا كان X (أنه يبلغ من العمر 26 عامًا ويكسب 2000 دولار).
- الاحتمال - P (X | H) هو احتمال الاحتمال. في هذه الحالة ، نظرًا لأننا نعلم أن العميل سيشتري الكتاب ، فإن الاحتمالية هي احتمال أن يكون العميل يبلغ من العمر 26 عامًا ويحصل على دخل قدره 2000 دولار.
بالنظر إلى هذه ، تنص نظرية بايز:
الفوسفور (H | X) = [P (X | H) * P (H)] / P (X)
لاحظ ظهور المصطلحات الأربعة أعلاه في النظرية - الاحتمال الخلفي ، الاحتمالية الاحتمالية ، الاحتمال السابق ، والأدلة.
قراءة: شرح بايز ساذج
كيفية تطبيق نظرية بايز في التعلم الآلي
يتم استخدام Naive Bayes Classifier ، وهو نسخة مبسطة من نظرية بايز ، كخوارزمية تصنيف لتصنيف البيانات إلى فئات مختلفة بدقة وسرعة.
دعونا نرى كيف يمكن تطبيق مصنف Naive Bayes كخوارزمية تصنيف.
- ضع في اعتبارك مثالًا عامًا: X عبارة عن متجه يتكون من سمات 'n' ، أي X = {x1، x2، x3،…، xn}.
- لنفترض أن لدينا فئات "m" {C1، C2،…، Cm}. يجب أن يتنبأ المصنف الخاص بنا بأن X ينتمي إلى فئة معينة. سيتم اختيار الفئة التي تقدم أعلى احتمالية لاحقة كأفضل فئة. لذا من الناحية الرياضية ، سيتنبأ المصنف بالفئة Ci iff P (Ci | X)> P (Cj | X). تطبيق نظرية بايز:
P (Ci | X) = [P (X | Ci) * P (Ci)] / P (X)
- P (X) ، كونها مستقلة عن الحالة ، ثابتة لكل فئة. لذلك لتعظيم P (Ci | X) ، يجب تعظيم [P (X | Ci) * P (Ci)]. بالنظر إلى احتمال حدوث كل فئة على حد سواء ، لدينا P (C1) = P (C2) = P (C3)… = P (Cn). لذا في النهاية ، نحتاج إلى تعظيم P (X | Ci) فقط.
- نظرًا لأنه من المحتمل أن تحتوي مجموعة البيانات الكبيرة النموذجية على العديد من السمات ، فمن المكلف من الناحية الحسابية إجراء عملية P (X | Ci) لكل سمة. هذا هو المكان الذي يأتي فيه الاستقلال الشرطي الطبقي لتبسيط المشكلة وتقليل تكاليف الحساب. من خلال الاستقلال الشرطي الطبقي ، فإننا نعني أننا نعتبر قيم السمة مستقلة عن بعضها البعض بشكل مشروط. هذا هو تصنيف بايز السذاجة.
الفوسفور (Xi | C) = P (x1 | C) * P (x2 | C) * ... * P (xn | C)
أصبح من السهل الآن حساب الاحتمالات الأصغر. هناك شيء مهم يجب ملاحظته هنا: نظرًا لأن xk ينتمي إلى كل سمة ، نحتاج أيضًا إلى التحقق مما إذا كانت السمة التي نتعامل معها قاطعة أم مستمرة .
- إذا كانت لدينا سمة فئوية ، فإن الأمور أبسط. يمكننا فقط حساب عدد مثيلات الفئة Ci التي تتكون من القيمة xk للسمة k ثم نقسمها على عدد مثيلات الفئة Ci.
- إذا كانت لدينا سمة مستمرة ، مع الأخذ في الاعتبار أن لدينا دالة توزيع عادية ، فإننا نطبق الصيغة التالية ، بمتوسط؟ والانحراف المعياري؟:
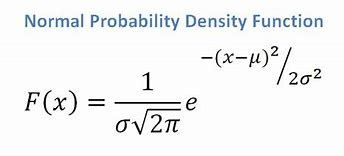

مصدر
في النهاية ، سيكون لدينا P (x | Ci) = F (xk،؟ k،؟ k).
- الآن ، لدينا جميع القيم التي نحتاجها لاستخدام نظرية بايز لكل فئة Ci. سيكون صنفنا المتوقع هو الفئة التي تحقق أعلى احتمال P (X | Ci) * P (Ci).
مثال: التصنيف التنبؤي لعملاء محل لبيع الكتب
لدينا مجموعة البيانات التالية من متجر كتب:
| سن | دخل | طالب علم | التصنيف الائتماني | Buys_Book |
| شباب | متوسط | رقم | معرض | رقم |
| شباب | متوسط | رقم | ممتاز | رقم |
| متوسط العمر | متوسط | رقم | معرض | نعم |
| كبير | متوسط | رقم | معرض | نعم |
| كبير | قليل | نعم | معرض | نعم |
| كبير | قليل | نعم | ممتاز | رقم |
| متوسط العمر | قليل | نعم | ممتاز | نعم |
| شباب | متوسط | رقم | معرض | رقم |
| شباب | قليل | نعم | معرض | نعم |
| كبير | متوسط | نعم | معرض | نعم |
| شباب | متوسط | نعم | ممتاز | نعم |
| متوسط العمر | متوسط | رقم | ممتاز | نعم |
| متوسط العمر | متوسط | نعم | معرض | نعم |
| كبير | متوسط | رقم | ممتاز | رقم |
لدينا سمات مثل العمر والدخل والطالب والتصنيف الائتماني. فصلنا ، buys_book ، له نتيجتان: نعم أو لا.
هدفنا هو التصنيف على أساس السمات التالية:
X = {العمر = الشباب ، الطالب = نعم ، الدخل = متوسط ، credit_rating = عادل}.
كما أوضحنا سابقًا ، لتعظيم P (Ci | X) ، نحتاج إلى تعظيم [P (X | Ci) * P (Ci)] من أجل i = 1 و i = 2.
ومن ثم ، ف (buys_book = نعم) = 9/14 = 0.643
P (buys_book = no) = 5/14 = 0.357
ف (العمر = الشباب | buys_book = نعم) = 2/9 = 0.222
ف (العمر = الشباب | buys_book = لا) = 3/5 = 0.600
الفوسفور (الدخل = متوسط | buys_book = نعم) = 4/9 = 0.444
الفوسفور (الدخل = متوسط | buys_book = لا) = 2/5 = 0.400
ف (الطالب = نعم | buys_book = نعم) = 6/9 = 0.667
ف (الطالب = نعم | buys_book = لا) = 1/5 = 0.200
ف (Credit_rating = عادل | buys_book = نعم) = 6/9 = 0.667
P (معدل الائتمان = عادل | buys_book = لا) = 2/5 = 0.400
باستخدام الاحتمالات المحسوبة أعلاه ، لدينا
P (X | buys_book = نعم) = 0.222 × 0.444 × 0.667 × 0.667 = 0.044
بصورة مماثلة،
P (X | buys_book = no) = 0.600 × 0.400 × 0.200 × 0.400 = 0.019
ما هي الفئة التي يوفرها Ci الحد الأقصى P (X | Ci) * P (Ci)؟ نحسب:
P (X | buys_book = نعم) * P (buys_book = نعم) = 0.044 × 0.643 = 0.028
P (X | buys_book = لا) * P (buys_book = لا) = 0.019 × 0.357 = 0.007

بمقارنة الاثنين أعلاه ، نظرًا لأن 0.028> 0.007 ، يتوقع Naive Bayes Classifier أن العميل الذي يمتلك السمات المذكورة أعلاه سيشتري كتابًا.
الدفع: أفكار ومواضيع لمشروع التعلم الآلي
هل مصنف بايزي طريقة جيدة؟
توفر الخوارزميات المستندة إلى نظرية بايز في التعلم الآلي نتائج قابلة للمقارنة مع الخوارزميات الأخرى ، وتعتبر المصنفات البايزية عمومًا طرقًا بسيطة عالية الدقة. ومع ذلك ، يجب الحرص على تذكر أن المصنفات البايزية مناسبة بشكل خاص عندما يكون افتراض الاستقلال الشرطي للطبقة صحيحًا ، وليس في جميع الحالات. مصدر قلق عملي آخر هو أن الحصول على جميع البيانات الاحتمالية قد لا يكون دائمًا ممكنًا.
خاتمة
نظرية بايز لها العديد من التطبيقات في التعلم الآلي ، لا سيما في المشاكل القائمة على التصنيف. يتضمن تطبيق هذه المجموعة من الخوارزميات في التعلم الآلي الإلمام بمصطلحات مثل الاحتمال السابق والاحتمال اللاحق. في هذه المقالة ، ناقشنا أساسيات نظرية بايز ، واستخدامها في مشاكل التعلم الآلي ، وعملنا من خلال مثال على التصنيف.
نظرًا لأن نظرية بايز تشكل جزءًا مهمًا من الخوارزميات القائمة على التصنيف في التعلم الآلي ، يمكنك معرفة المزيد حول برنامج الشهادات المتقدمة من upGrad في التعلم الآلي ومعالجة اللغات الطبيعية . تم تصميم هذه الدورة التدريبية مع مراعاة أنواع مختلفة من الطلاب المهتمين بالتعلم الآلي ، حيث تقدم إرشادًا من 1-1 وغير ذلك الكثير.
لماذا نستخدم نظرية بايز في التعلم الآلي؟
نظرية بايز هي طريقة لحساب الاحتمالات الشرطية ، أو احتمالية وقوع حدث إذا حدث آخر سابقًا. يمكن أن يؤدي الاحتمال الشرطي إلى نتائج أكثر دقة من خلال تضمين شروط إضافية - بمعنى آخر ، المزيد من البيانات. من أجل الحصول على التقديرات والاحتمالات الصحيحة في التعلم الآلي ، فإن الاحتمالات المشروطة مطلوبة. نظرًا لانتشار المجال المتزايد عبر مجموعة واسعة من المجالات ، من الأهمية بمكان فهم أهمية الخوارزميات والأساليب مثل نظرية بايز في التعلم الآلي.
هل مصنف بايزي اختيار جيد؟
في التعلم الآلي ، تنتج الخوارزميات المستندة إلى نظرية بايز نتائج مماثلة لتلك الخاصة بالطرق الأخرى ، ويُنظر إلى المصنفات البايزية على نطاق واسع على أنها مناهج بسيطة عالية الدقة. ومع ذلك ، من المهم أن تضع في اعتبارك أنه من الأفضل استخدام مصنفات بايز عندما تكون حالة الاستقلال الشرطي للطبقة صحيحة ، وليس في جميع الظروف. هناك اعتبار آخر وهو أن الحصول على جميع بيانات الاحتمالية قد لا يكون دائمًا ممكنًا.
كيف يمكن تطبيق نظرية بايز عمليا؟
تحسب نظرية بايز احتمالية الحدوث بناءً على أدلة جديدة مرتبطة بها أو يمكن أن تكون مرتبطة بها. يمكن أيضًا استخدام الطريقة لمعرفة كيفية تأثير المعلومات الجديدة الافتراضية على احتمالية وقوع حدث ما ، بافتراض صحة المعلومات الجديدة. خذ ، على سبيل المثال ، بطاقة واحدة مختارة من مجموعة من 52 بطاقة. احتمال أن تصبح البطاقة ملكًا هو 4 مقسومًا على 52 ، أو 1/13 ، أو ما يقرب من 7.69 بالمائة. ضع في اعتبارك أن السطح يحتوي على أربعة ملوك. لنفترض أنه تم الكشف عن أن البطاقة المختارة هي بطاقة وجه. نظرًا لوجود 12 بطاقة وجه في مجموعة أوراق اللعب ، فإن احتمال أن تكون البطاقة المختارة ملكًا هو 4 مقسومًا على 12 ، أو ما يقرب من 33.3 بالمائة.
