شرح نظرية بايز بمثال - دليل كامل

مقدمة

ما هي نظرية بايز؟

تُستخدم نظرية بايز لحساب الاحتمال الشرطي حيث يفشل الحدس غالبًا. على الرغم من استخدامها على نطاق واسع في الاحتمالات ، يتم تطبيق النظرية في مجال التعلم الآلي أيضًا. يتضمن استخدامه في التعلم الآلي ملاءمة نموذج لمجموعة بيانات التدريب وتطوير نماذج التصنيف.

ما هو الاحتمال الشرطي؟

عادة ما يتم تعريف الاحتمال الشرطي على أنه احتمال وقوع حدث واحد في ضوء وقوع حدث آخر.

• إذا كان A و B حدثين ، فسيكون الاحتمال الشرطي هو P (A معطى B) أو P (A | B).
• يمكن حساب الاحتمال الشرطي من الاحتمال المشترك (A | B) = P (A، B) / P (B)

• الاحتمال الشرطي غير متماثل ؛ على سبيل المثال P (A | B)! = P (B | A)

تتضمن الطرق الأخرى لحساب الاحتمال الشرطي استخدام الاحتمال الشرطي الآخر ، أي

الفوسفور (A | B) = P (B | A) * P (A) / P (B)

يستخدم العكس أيضا

الفوسفور (B | A) = P (A | B) * P (B) / P (A)

تكون طريقة الحساب هذه مفيدة عندما يكون من الصعب حساب الاحتمال المشترك. عدا ذلك ، عندما يكون الاحتمال الشرطي العكسي متاحًا ، يصبح الحساب من خلال ذلك سهلاً.

يشار إلى هذا الحساب البديل للاحتمال الشرطي باسم قاعدة بايز أو نظرية بايز. تم تسميته تحت الشخص الذي وصفه لأول مرة ، "القس توماس بايز".

صيغة نظرية بايز

نظرية بايز هي طريقة لحساب الاحتمال الشرطي عندما لا يتوفر الاحتمال المشترك. في بعض الأحيان ، لا يمكن الوصول إلى المقام مباشرة. في مثل هذه الحالات ، تكون الطريقة البديلة للحساب كما يلي:

P (B) = P (B | A) * P (A) + P (B | ليس A) * P (ليس A)

هذه هي صياغة نظرية بايز التي تظهر حسابًا بديلًا لـ P (B).

الفوسفور (A | B) = P (B | A) * P (A) / P (B | A) * P (A) + P (B | ليس A) * P (ليس A)

يمكن وصف الصيغة أعلاه بوضع أقواس حول المقام

الفوسفور (أ | ب) = ف (ب | أ) * ف (أ) / (ف (ب | أ) * ف (أ) + ف (ب | لا أ) * ف (لا أ))

أيضًا ، إذا كان لدينا P (A) ، فيمكن حساب P (وليس A) على النحو التالي

الفوسفور (لا أ) = 1 - ف (أ)

وبالمثل ، إذا كان لدينا P (وليس B | وليس A) ، فيمكن حساب P (B | وليس A) على النحو التالي

الفوسفور (ب | لا أ) = 1 - ف (ليس ب | لا أ)

نظرية بايز للاحتمال الشرطي

تتكون نظرية بايز من عدة مصطلحات يتم إعطاء أسمائها بناءً على سياق تطبيقها في المعادلة.

يشير الاحتمال اللاحق إلى نتيجة P (A | B) ، ويشير الاحتمال السابق إلى P (A).

• P (A | B): الاحتمال الخلفي.
• P (A): الاحتمال المسبق.

وبالمثل ، يُشار إلى P (B | A) و P (B) على أنهما الاحتمال والأدلة.

• P (B | A): الاحتمال.
• ع (ب): الدليل.

لذلك ، يمكن إعادة صياغة نظرية بايز للاحتمال الشرطي على النحو التالي:

اللاحق = احتمال * سابق / دليل

إذا كان علينا حساب احتمال وجود حريق بالنظر إلى وجود دخان ، فسيتم استخدام المعادلة التالية:

P (Fire | Smoke) = P (Smoke | Fire) * P (Fire) / P (Smoke)

حيث ، P (النار) هي السابقة ، P (دخان | حريق) هو الاحتمال ، و P (دخان) هو الدليل.

رسم توضيحي لنظرية بايز

يتم وصف مثال نظرية بايز لتوضيح استخدام نظرية بايز في مشكلة.

مشكلة

توجد ثلاثة مربعات مكتوب عليها A و B و C. تفاصيل الصناديق هي:

• صندوق أ يحتوي على 2 كرات حمراء و 3 كرات سوداء
• يحتوي الصندوق ب على 3 كرة حمراء و 1 كرة سوداء
• والمربع C يحتوي على كرة حمراء و 4 كرات سوداء

جميع الصناديق الثلاثة متطابقة ولها احتمالية متساوية لالتقاطها. إذن ، ما هو احتمال أن تكون الكرة الحمراء قد التقطت من الصندوق أ؟

المحلول

لنفترض أن E تدل على حدث التقاط كرة حمراء وأن A و B و C تدل على أن الكرة التقطت من الصناديق الخاصة بكل منها. لذلك فإن الاحتمال الشرطي هو P (A | E) الذي يجب حسابه.

الاحتمالات الحالية P (A) = P (B) = P (C) = 1/3 ، نظرًا لأن جميع الصناديق لها احتمالية متساوية في الاختيار.

P (E | A) = عدد الكرات الحمراء في المربع A / إجمالي عدد الكرات في المربع A = 2/5

وبالمثل ، P (E | B) = 3/4 و P (E | C) = 1/5

ثم الدليل P (E) = P (E | A) * P (A) + P (E | B) * P (B) + P (E | C) * P (C)

= (2/5) * (1/3) + (3/4) * (1/3) + (1/5) * (1/3) = 0.45

لذلك ، P (A | E) = P (E | A) * P (A) / P (E) = (2/5) * (1/3) / 0.45 = 0.296

مثال على نظرية بايز

تعطي نظرية بايز احتمال وقوع "حدث" بالمعلومات المعطاة عن "الاختبارات".

• هناك فرق بين "الأحداث" و "الاختبارات". على سبيل المثال ، هناك اختبار لمرض الكبد ، والذي يختلف عن الإصابة بمرض الكبد ، أي حدث.
• قد يكون للأحداث النادرة معدل إيجابي خاطئ أعلى.

مثال 1

ما هو احتمال إصابة المريض بأمراض الكبد إذا كان مدمنًا على الكحول؟

هنا ، "كونك مدمن على الكحول" هو "الاختبار" (نوع اختبار عباد الشمس) لأمراض الكبد.

• A هو الحدث ، أي "المريض يعاني من مرض في الكبد" ".

حسب السجلات السابقة للعيادة ، فإن 10٪ من المرضى الذين يدخلون العيادة يعانون من أمراض الكبد.

لذلك ، P (A) = 0.10

• B هو اختبار عباد الشمس أن "المريض مدمن على الكحول".

أظهرت السجلات السابقة للعيادة أن 5٪ من المرضى الذين يدخلون العيادة مدمنون على الكحول.

لذلك ، P (B) = 0.05

• كما أن 7٪ من مرضى الكبد مدمنون على الكحول. هذا يحدد B | A: احتمال أن يكون المريض مدمنًا على الكحول ، نظرًا لإصابته بمرض في الكبد هو 7 ٪.

وفقًا لصيغة نظرية بايز ،

الفوسفور (أ | ب) = (0.07 * 0.1) /0.05 = 0.14

لذلك ، بالنسبة للمريض الذي يعاني من إدمان الكحول ، فإن فرص الإصابة بأمراض الكبد هي 0.14 (14٪).

مثال 2

• الحرائق الخطيرة نادرة (1٪)
• لكن الدخان شائع إلى حد ما (10٪) بسبب حفلات الشواء ،
• و 90٪ من الحرائق الخطرة تصنع دخاناً

ما هو احتمال نشوب حريق خطير عند وجود دخان؟

عملية حسابية

الفوسفور (حريق | دخان) = ف (حريق) ف (دخان | حريق) / ف (دخان)

= 1٪ × 90٪ / 10٪

= 9٪

مثال 3

ما هي فرصة هطول المطر خلال النهار؟ حيث ، المطر يعني المطر أثناء النهار ، والسحابة تعني الصباح الملبد بالغيوم.

يتم كتابة فرصة هطول الأمطار نظرًا للسحابة P (مطر | سحابة)

P (مطر | سحابة) = P (مطر) P (سحابة | مطر) / P (سحابة)

P (المطر) هو احتمال هطول الأمطار = 10٪

P (Cloud | Rain) هو احتمال حدوث سحابة ، بالنظر إلى أن المطر يحدث = 50٪

P (سحابة) هو احتمال وجود سحابة = 40٪

P (مطر | سحابة) = 0.1 × 0.5 / 0.4 = .125

لذلك ، فإن احتمال هطول أمطار 12.5٪.

التطبيقات

توجد عدة تطبيقات لنظرية بايز في العالم الحقيقي. التطبيقات الرئيسية القليلة للنظرية هي:

1. فرضيات النمذجة

تجد نظرية بايز تطبيقًا واسعًا في التعلم الآلي المطبق وتؤسس علاقة بين البيانات والنموذج. يستخدم التعلم الآلي التطبيقي عملية اختبار وتحليل الفرضيات المختلفة في مجموعة بيانات معينة.

لوصف العلاقة بين البيانات والنموذج ، توفر نظرية بايز نموذجًا احتماليًا.

الفوسفور (ح | د) = ف (د | ح) * ف (ح) / ف (د)

أين،

P (h | D): الاحتمال الخلفي للفرضية

P (h): الاحتمال السابق للفرضية.

تؤدي الزيادة في P (D) إلى تقليل P (h | D). على العكس من ذلك ، إذا زادت P (h) واحتمال مراقبة البيانات المعطاة ، فإن احتمال P (h | D) يزداد.

2. نظرية بايز للتصنيف

تتضمن طريقة التصنيف وضع العلامات على بيانات معينة. يمكن تعريفه على أنه حساب الاحتمال الشرطي لتسمية فئة بالنظر إلى عينة بيانات.

P (فئة | بيانات) = (P (بيانات | فئة) * P (فئة)) / P (بيانات)

حيث P (class | data) هو احتمال الفئة بالنظر إلى البيانات المقدمة.

يمكن إجراء الحساب لكل فئة. يمكن إسناد الفئة ذات الاحتمال الأكبر إلى بيانات الإدخال.

حساب الاحتمال الشرطي غير ممكن في ظل ظروف عدد قليل من الأمثلة. لذلك ، فإن التطبيق المباشر لنظرية بايز غير ممكن. يكمن حل نموذج التصنيف في الحساب المبسط.

• مصنف بايز ساذج

تعتبر نظرية بايز أن متغيرات الإدخال تعتمد على متغيرات أخرى تسبب تعقيد الحساب. لذلك ، يتم إزالة الافتراض ويعتبر كل متغير إدخال متغيرًا مستقلاً. نتيجة لذلك ، يتغير النموذج من الاعتماد إلى نموذج الاحتمال الشرطي المستقل. إنه يقلل في النهاية من التعقيد.

يشار إلى هذا التبسيط لنظرية بايز باسم Naive Bayes. يستخدم على نطاق واسع في نماذج التصنيف والتنبؤ.

• مصنف بايز الأمثل

هذا نوع من النماذج الاحتمالية التي تتضمن التنبؤ بمثال جديد بالنظر إلى مجموعة بيانات التدريب. أحد الأمثلة على مصنف Bayes الأمثل هو "ما هو التصنيف الأكثر احتمالية للمثيل الجديد بالنظر إلى بيانات التدريب؟"

يمكن حساب الاحتمال الشرطي لمثيل جديد بالنظر إلى بيانات التدريب من خلال المعادلة التالية

P (vj | D) = sum {h في H} P (vj | hi) * P (hi | D)

حيث vj هو مثيل جديد ليتم تصنيفه ،

H هي مجموعة الفرضيات لتصنيف المثال ،

مرحبا هي فرضية معينة ،

P (vj | hi) هو الاحتمال اللاحق لـ vi معطى فرضية hi و

P (hi | D) هو الاحتمال اللاحق للفرضية hi في ضوء البيانات D.

3. استخدامات نظرية بايز في التعلم الآلي

التطبيق الأكثر شيوعًا لنظرية بايز في التعلم الآلي هو تطوير مشاكل التصنيف. تشمل التطبيقات الأخرى بدلاً من التصنيف التحسين والنماذج غير الرسمية.

• التحسين بايزي

إنها دائمًا مهمة قابلة للتحدي للعثور على إدخال ينتج عنه التكلفة الدنيا أو القصوى لوظيفة موضوعية معينة. يعتمد تحسين Bayesian على نظرية Bayes ويوفر جانبًا للبحث عن مشكلة تحسين عالمية. تتضمن الطريقة بناء نموذج احتمالي (وظيفة بديلة) ، والبحث من خلال وظيفة اكتساب ، واختيار العينات المرشحة لتقييم وظيفة الهدف الحقيقية.

في التعلم الآلي التطبيقي ، يتم استخدام تحسين Bayesian لضبط المعلمات الفائقة لنموذج جيد الأداء.

• شبكات عقيدة بايزي

يمكن تحديد العلاقات بين المتغيرات من خلال استخدام النماذج الاحتمالية. يتم استخدامها أيضًا لحساب الاحتمالات. قد لا يتمكن نموذج الاحتمال المشروط بالكامل من حساب الاحتمالات بسبب الحجم الكبير للبيانات. قام Naive Bayes بتبسيط نهج الحساب. توجد طريقة أخرى حيث يتم تطوير نموذج بناءً على الاعتماد الشرطي المعروف بين المتغيرات العشوائية والاستقلال الشرطي في حالات أخرى. تعرض شبكة بايز هذا الاعتماد والاستقلالية من خلال نموذج الرسم البياني الاحتمالي ذي الحواف الموجهة. يتم عرض التبعية الشرطية المعروفة كحواف موجهة وتمثل الاتصالات المفقودة الاستقلالية الشرطية في النموذج.

4. تصفية البريد الإلكتروني العشوائي بايزي

تصفية البريد العشوائي هو تطبيق آخر لنظرية بايز. يوجد حدثان:

• الحدث أ: الرسالة بريد عشوائي.
• اختبار X: الرسالة تحتوي على كلمات معينة (X)

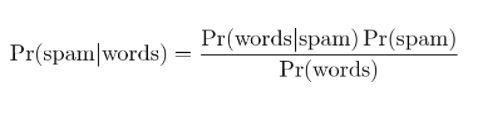
من خلال تطبيق نظرية بايز ، يمكن توقع ما إذا كانت الرسالة بريد عشوائي في ضوء "نتائج الاختبار". يمكن أن يحسب تحليل الكلمات في رسالة احتمالات أن تكون رسالة بريد عشوائي. من خلال تدريب المرشحات مع الرسائل المتكررة ، يتم تحديث حقيقة أن احتمال وجود كلمات معينة في الرسالة سيكون بريدًا عشوائيًا.

تطبيق لنظرية بايز مع مثال

ينتج منتج المحفز جهازًا لاختبار العيوب في محفز كهربائي معين (EC). يدعي منتج المحفز أن الاختبار موثوق به بنسبة 97٪ إذا كان EC معيبًا وموثوقًا بنسبة 99٪ عندما لا تشوبه شائبة. ومع ذلك ، قد يُتوقع أن تكون نسبة 4٪ من المجموعة الأوروبية المذكورة معيبة عند التسليم. يتم تطبيق قاعدة Bayes للتأكد من الموثوقية الحقيقية للجهاز. مجموعات الحدث الأساسية هي

ج: المفوضية الأوروبية معيبة ؛ أ: المفوضية الأوروبية لا تشوبها شائبة ؛ ب: تم ​​اختبار المجموعة الأوروبية على أنها معيبة ؛ ب ': تم اختبار المجموعة الأوروبية لتكون خالية من العيوب.

ستكون الاحتمالات

B / A: EC (معروف أنها) معيبة ، وتم اختبارها معيبة ، P (B / A) = 0.97 ،

B '/ A: EC (معروف أنه) معيب ، لكن تم اختباره لا تشوبه شائبة ، P (B' / A) = 1-P (B / A) = 0.03 ،

B / A ': EC (معروف أنه) معيب ، لكن تم اختباره معيب ، P (B / A') = 1- P (B '/ A') = 0.01

B '/ A: = EC (معروف أنه) لا تشوبه شائبة ، وتم اختباره لا تشوبه شائبة P (B' / A ') = 0.99

الاحتمالات التي تحسبها نظرية بايز هي:

تُظهر احتمالية الحساب أن هناك احتمالًا كبيرًا لرفض EC's الذي لا تشوبه شائبة (حوالي 20٪) واحتمال ضعيف لتحديد الموصلات المعيبة (حوالي 80٪).

خاتمة

واحدة من السمات الأكثر لفتا للنظر في نظرية بايز هي أنه من خلال نسب احتمالية قليلة ، يمكن الحصول على قدر هائل من المعلومات. مع وسائل الاحتمال ، يمكن أن يتحول احتمال حدث سابق إلى الاحتمال اللاحق. يمكن تطبيق مناهج نظرية بايز في مجالات الإحصاء ونظرية المعرفة والمنطق الاستقرائي.

إذا كنت مهتمًا بمعرفة المزيد حول نظرية بايز والذكاء الاصطناعي والتعلم الآلي ، فراجع برنامج IIIT-B & upGrad's Executive PG في التعلم الآلي والذكاء الاصطناعي المصمم للمهنيين العاملين ويقدم أكثر من 450 ساعة من التدريب الصارم ، وأكثر من 30 حالة دراسات ومهام ، حالة خريجي IIIT-B ، أكثر من 5 مشاريع تتويجا عملية ومساعدة وظيفية مع كبرى الشركات.